安徽省芜湖一中2013届高三上学期第二次模拟考试数学文试卷

安徽省芜湖一中2013届高三上学期第二次模拟考试数学文试卷

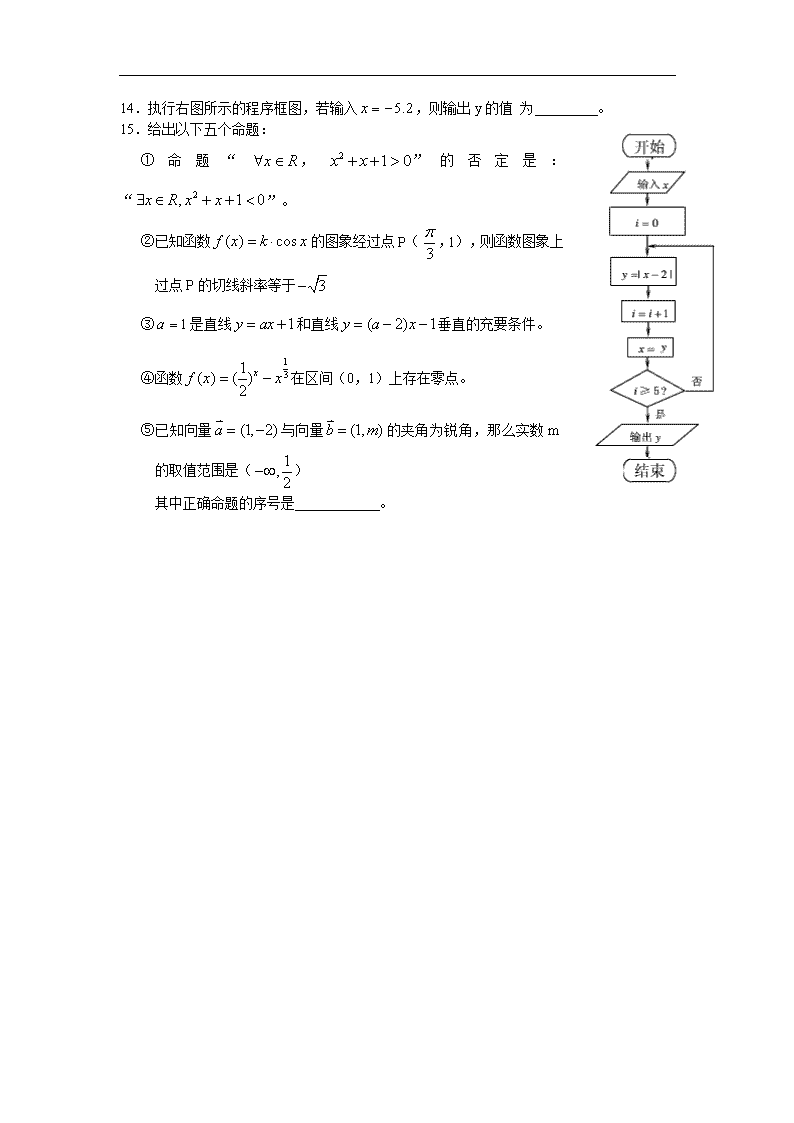
芜湖一中2013届高三第二次模拟考试 数学（文科）试题 第I卷（选择题 共50分）‎ 一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．已知集合，，且，则实数m的取值范围是（ ）‎ ‎ A． B． C． D．‎ ‎2．已知复数（），且有，是z的共轭复数，那么的值为（ ）‎ ‎ A． B． C． D．‎ ‎3．若，，，且，那么与的夹角为（ ）‎ ‎ A． B． C． D．‎ ‎4．已知圆c与直线及都相切，圆心在直线上，则圆c的方程为（ ）‎ ‎ A． B．‎ C． D．‎ ‎5．已知是等差数列，，，那么该数列的前13项和等于（ ）‎ ‎ A．156 B．‎132 ‎ C．110 D．100‎ ‎6．已知函数，是定义在R上的奇函数，当时，，则函数的大致图象为（ ）‎ ‎7．设变量x，y满足约束条件，则目标函数的最小值为（ ）‎ ‎ A．9 B．‎4 ‎ C．3 D．2‎ ‎8．一个几何体的三视图如图所示，则该几何体的体积为（ ）‎ ‎ A． ‎ B． ‎ C． ‎ D．‎ ‎10．五张卡片上分别写有数字1，2，3，4，5，从这五张卡片中随机抽取2张，则取出的2张卡片上数字之和为奇数的概率为（ ）‎ ‎ A． B． C． D．‎ 第II卷（非选择题　　共100分）‎ 二、填空题（本大题共5小题，每小题5分，共25分）‎ ‎11．抛物线的焦点坐标为 。‎ ‎12．已知x，y的值如下表所示：‎ x ‎2‎ ‎3‎ ‎4‎ y ‎5‎ ‎4‎ ‎6‎ ‎ 如果y与x呈线性相关且回归直线方程为，那么b= 。‎ ‎13．某长方体的对角线长是4，有一条棱长为1，那么该长方体的最大体积为 。‎ ‎14．执行右图所示的程序框图，若输入，则输出y的值 为 。‎ ‎15．给出以下五个命题：‎ ‎ ①命题“，”的否定是：“”。‎ ‎②已知函数的图象经过点P（，1），则函数图象上过点P的切线斜率等于 ‎③是直线和直线垂直的充要条件。‎ ‎④函数在区间（0，1）上存在零点。‎ ‎⑤已知向量与向量的夹角为锐角，那么实数m的取值范围是（）‎ 其中正确命题的序号是 。‎ 芜湖一中2013届高三第二次模拟考试 数学（文科）答题卷 一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 二、填空题（本大题共5小题，每小题5分，共25分）‎ ‎11． 12． 13． ‎ ‎14． 15． ‎ 三、解答题（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤）‎ ‎16．（本大题满分13分）‎ ‎ 已知，，若，求：‎ ‎ （1）的最小正周期及对称轴方程。‎ ‎ （2）的单调递增区间。‎ ‎ （3）当时，函数的值域。‎ ‎17．（本大题满分12分）‎ ‎ 如图，四棱锥P-ABCD的底面是正方形，PD面ABCD，E是PD上一点。‎ ‎ （1）求证：ACBE。‎ ‎ （2）若PD=AD=1，且的余弦值为，求三棱锥E-PBC的体积。‎ ‎18．（本大题满分12分）‎ ‎ 某省对省内养殖场“瘦肉精”使用情况进行检查，在全省的养殖场随机抽取M个养殖场的猪作为样本，得到M个养殖场“瘦肉精”检测阳性猪的头数，根据此数据作出了频率分布表和频率分布直方图如下：‎ ‎ ‎ 分组 频数 频率 ‎10‎ ‎0.25‎ ‎24‎ n m P ‎2‎ ‎0.05‎ 合计 M ‎1‎ ‎（1）求出表中M，P以及图中a的值。‎ ‎ （2）若该省有这样规模的养殖场240个，试估计该省“瘦肉精”检测呈阳性的猪的头数在区间内的养殖场的个数。‎ ‎ （3）在所取样本中，出现“瘦肉精”呈阳性猪的头数不少于20头的养殖场中任选2个，求至多一个养殖场出现“瘦肉精”阳性猪头数在区间内的概率。‎ ‎19．（本大题满分12分）‎ ‎ 设函数 ‎ （1）若函数在处取得极值-2，求a，b的值。‎ ‎ （2）若函数在区间（-1，1）内单调递增，求b的取值范围。‎ ‎20．（本大意满分13分）‎ ‎ 已知数列的前n项和为，且满足各项为正数的数列中，对一切，有，且，，。‎ ‎ （1）求数列和的通项公式。‎ ‎ （2）设数列的前n项和为，求。‎ ‎21．（本大题满分13分）‎ ‎ 在平面直线坐标系XOY中，给定两点A（1，0），B（0，-2），点C满足，其中，且。‎ ‎ （1）求点C的轨迹方程。‎ ‎ （2）设点C的轨迹与双曲线（）相交于M，N两点，且以MN为直径的圆经过原点，求证：是定值。‎ ‎ （3）在（2）条件下，若双曲线的离心率不大于，求该双曲线实轴的取值范围。‎ 高三数学答案（文科）‎ 一、 选择题：（每题5分、共50分）‎ ‎1．C． 又 ‎ ‎2．B． ‎ ‎ ‎ ‎3．B ‎ ‎ ‎ ‎4．D 园心在直线上 排除 又选项C中园心到直线的距离等于排除C。‎ ‎5．A 两式相加： ‎ ‎6．D 偶函数 奇函数 是奇函数排除；又当取较大正数时， 排除C故选D ‎7．C 代入 ‎8．A 该几何体下面是个园柱，上面是个三棱锥，其体积为 ‎ 选 ‎9．B ‎ 在上减 在[-1，0]上减，又偶函数 在上增 ‎ 是钝角三角形的两个锐角 选B ‎10.A ‎ ‎11. 焦点在轴上。‎ ‎12． 而 ‎ ‎13． ‎ ‎14．0.8（略）‎ ‎15．②③④ ①错，应为“”， ②中 ‎ ‎ 斜率 正确 ③正确显然 ‎④中， 有零点，正确 ⑤错 ‎ 三、解答题 ‎16．解：‎ ‎……………………4分 ‎（1）………………5分 对称轴方程：…………7分 ‎（2）增即为的减 ………10分 ‎（3） ‎ 值域为………………13分 ‎17．解：（1）连接BD 是正方形 又面 ‎ 面 又BE面PBD ‎……………………6分 ‎（2）设，则 又 ‎ 中，由余弦定理解为：‎ ‎ ………………12分 ‎18．（1）由知： ‎ ‎ ……………………4分 ‎（2）养殖场有240个，分组[10，15]内的频率是0.25 估计全省在此区间内养殖场的个数为个…………………………7分 ‎（3）设在区间内的养殖场为，在区间内的为 任选2个养殖场共 （） （） （）（）（）（）‎ ‎（）（）（）（）（）（）（）（）共15种情况，而两个养殖场都在区间内只有一种 故所求概率……………………………………12分 ‎19．（1）依题意：……………………6分 ‎（2） 当时 函数在（-1，1）内不可能增，舍去 当 若时 ‎ 递增 故所求范围为………………12分 ‎20．（1） 时 当时 ‎ 成等比数列 ‎ 通项公式为： 即：…………4分 又对一切 ……………………①‎ 当时 ………………………②‎ ‎①—②得 ‎ 化简为 ‎ 用换上式中n得：‎ 两式相减整理得：即 ‎ 数列为等差数列 （当时） 又 数列（成等差数列） ………9分 ‎（2）错位相减得：……………13分 ‎21．（1）设C（）则 ………………3分 ‎（2）设M（）‎ N（）则，……………………6分 ‎ 韦达定理代入得 ‎ （定值）………………………………8分 ‎（3） …………………………10分 又 代入得 ‎ ……………………13分