- 2021-06-10 发布 |
- 37.5 KB |
- 7页

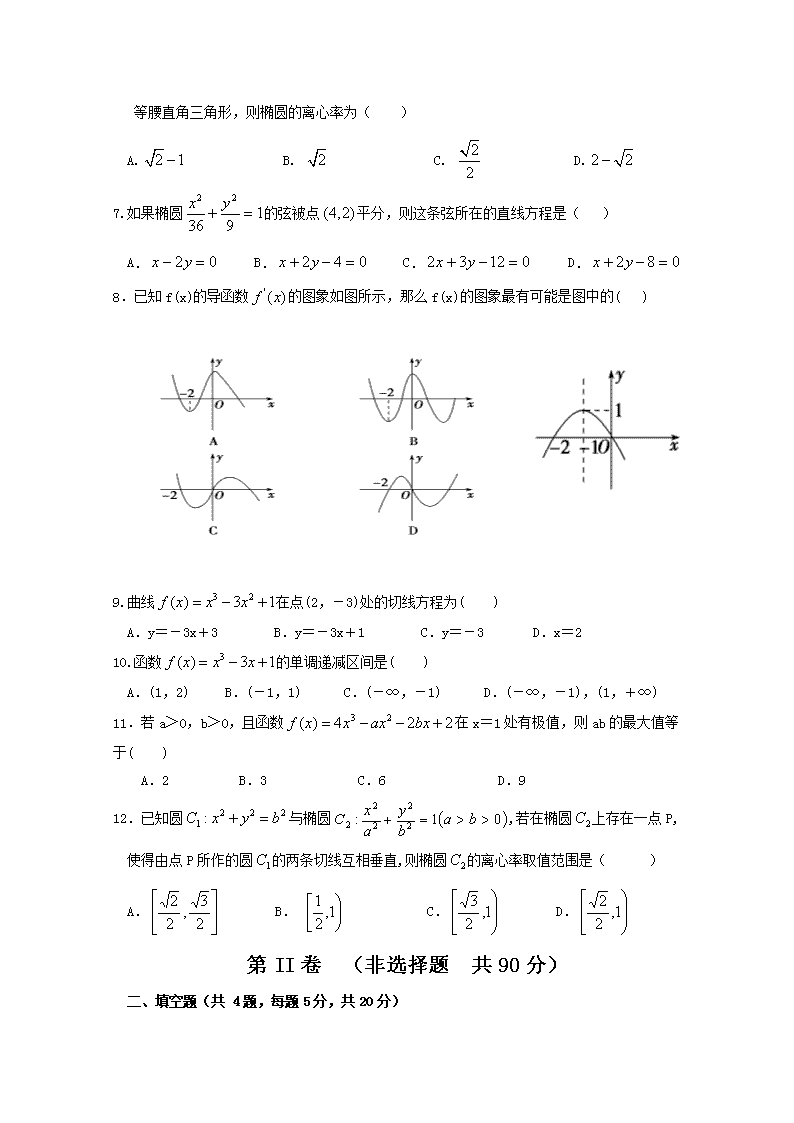

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年吉林省白城市通榆县第一中学高二上学期第三次月考数学(文)试题 Word版
2018-2019学年吉林省白城市通榆县第一中学高二上学期第三次月考数 学 文 科 试 卷 【注意事项】 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共2页22题,共120分; 2.请考生将自己的姓名、准考证号填写清楚,将条形码准确粘贴在条形码粘贴区; 3.请按题号顺序在各题目的答题区域内作答,在草稿纸、试题卷上答题无效,超出答题区域书写的答案无效,考试结束上交答题卡; 第Ⅰ卷 (选择题 共60分) 一、选择题(共12题,每题5分,共60分) 1. 命题“若A⊆B,则A=B”与其逆命题、否命题、逆否命题这四个命题中, 真命题的个数是( ) A.0 B.2 C.3 D.4 2.阅读下面程序框图,如果输出的函数值在区间 内, 则输入的实数x的取值范围 ( ) A.(-∞,2] B.[-2,-1] C.[-1,2] D.[2,+∞) 3.已知命题P:,则为( ) A. B. C. D. 4. 已知点在正的边上,,在边上任意取一点,则“的面积恰好小于面积的一半”的概率为 A. B. C. D. 5. “”是“方程表示椭圆”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 6. 为椭圆左右焦点,为椭圆上一点,垂直于轴,为 等腰直角三角形,则椭圆的离心率为( ) A. B. C. D. 7.如果椭圆的弦被点平分,则这条弦所在的直线方程是( ) A. B. C. D. 8.已知f(x)的导函数的图象如图所示,那么f(x)的图象最有可能是图中的( ) 9.曲线在点(2,-3)处的切线方程为( ) A.y=-3x+3 B.y=-3x+1 C.y=-3 D.x=2 10.函数的单调递减区间是( ) A.(1,2) B.(-1,1) C.(-∞,-1) D.(-∞,-1),(1,+∞) 11.若a>0,b>0,且函数在x=1处有极值,则ab的最大值等于( ) A.2 B.3 C.6 D.9 12.已知圆与椭圆,若在椭圆上存在一点P,使得由点P所作的圆的两条切线互相垂直,则椭圆的离心率取值范围是( ) A. B. C. D. 第II卷 (非选择题 共90分) 二、填空题(共 4题,每题5分,共20分) 13.若焦点在x轴的椭圆的离心率为,则实数m的值为 ___ 14. 已知是椭圆上的一点,是椭圆的两个焦点,当时,则 的面积为 . 15.已知函数在处的导数值为12,则n等于 16.当x∈[-1,2]时,恒成立,则实数m的取值范围是_ ___ 三、解答题(17题10分,其它每题12分,共70分) 17.已知p:方程所表示的曲线为焦点在轴上的椭圆; q:实数满足不等式 (1)若p为真,求实数的取值范围;(2)若p是q的充分不必要条件,求实数的取值范围 18. 求经过点(2,-3)且与椭圆有共同焦点的椭圆方程 19.已知曲线方程,求过点P(3,5)且与曲线相切的直线方程 20.某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人. (1)估计这所学校成绩在90~140分之间学生的参赛人数;参赛学生成绩的中位数、平均数(结果取整数) (2)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶学习小组.若选出的两人成绩之差大20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率 21.设函数在x=与x=-1处有极值 (1)写出函数的解析式;(2)求函数的单调区间;(3)求f(x)在[-1,2]上的最值. 22. 已知椭圆(a>b>0)的离心率e=,连接椭圆的四个顶点得到的菱形的面积 为4.(1)求椭圆的方程;(2)设直线与椭圆相交于不同的两点A、B,已知点A的坐标 为(-a,0).若,求直线的倾斜角. 高二年级上学期第三次质量检测 数 学 文 科 答 案 一、选择题 1.B 2.B 3.A 4.C 5.B 6.A 7.D 8.A 9.C 10.B 11. D 12.D 二、填空题 13. 14. 15. 3 16.m>2 三、解答题 17.解(1)∵方程所表示的曲线为焦点在x轴上的椭圆 ∴,解得: ∴t的那取值范围是 (2)∵命题q:实数满足不等式t2-(a-1)t-a<0,即(t+1)(t-a)<0. ∴当a>-1时,得到t∈(-1,a);当a<-1时,命题q为真命题得到t∈(a,-1) ∵命题P是命题q的充分不必要条件 ∴集合A={t|-1<t<1}是不等式t2-(a-1)t-a<0解集B的真子集 即:AB 解得:a>1 ∴a的那取值范围是a>1 18.解:化成标准形式,可得焦点坐标 ,<法一>设方程为把(2,-3)代入得 解得:,所以方程为 <法二>设方程为,把(2,-3)代入 解得k=6,所以方程为 19.解:P(3,5)不在曲线上,所以P不是切点,设切点坐标,∵,∴ ,切线方程为,P(3,5)在切线上得 解得 所以切线方程为或 即:或 20解:(1)∵130~140分数段的人数为2人,130~140分数段的频率为:0.005×10=0.05 ∴90~140分之间的人数为2÷0.05=40人, 设参赛学生成绩的中位数为x,∴参赛学生成绩的中位数的估计值为x, 0.01×10+0.025×10+(x-110) ×0.045=0.5,解得: 平均数=95×0.01×10+105×0.025×10+115×0.045×10+125×0.015×10+135×0.005×10=113 (2)第一组共有40×0.01×10=4人,记作:1,2,3,4 五组共有2人,记作:a,b 从第一组和第五组中任意选出两人共有下列15种选法: (1,2),(1,3),(1,4),(1,a),(1,b),(2,3),(2,4),(2,a),(2,b),(3,4),(3,a),(3,b), (4,a),(4,b),(a,b).共有15种结果, 设事件A:选出的两人为“黄金搭档组”.若两人成绩之差大于20,则两人分别来自于第一组和第五组,共有8种选法,故. 21解:(1) ,由题意得当x=与x=-1时函数有极值, 则x=与x=-1满足, 即 解得 所以 (2) 令,列表如下: x (-∞,-1) -1 y′ + 0 - 0 + y ↗ y极大值16 ↘ y极小值- ↗ 由上表可知(-∞,-1)和(,+∞)为函数的单调递增区间,为函数的单调递减区间. (3)因为f(-1)=16,f=-,f(2)=-11, 所以f(x)在[-1,2]上最小值是-,最大值为16. 22解:(1)由,得.再由,解得a=2b. 由题意可知,即ab=2. 解方程组得a=2,b=1 所以椭圆的方程为. (2) 由(1)可知点A的坐标是(-2,0)为左顶点,所以斜率一定存在 设点B的坐标为,直线l的斜率为k.则直线l的方程为 于是A、B两点的坐标满足方程组消去y并整理,得 . 由,得.从而. 所以. 由,得. 整理得,即,解得 所以直线l的倾斜角为或.查看更多