2021届课标版高考文科数学大一轮复习精练：§2-1 函数的概念及表示（试题部分）

2021届课标版高考文科数学大一轮复习精练：§2-1 函数的概念及表示（试题部分）

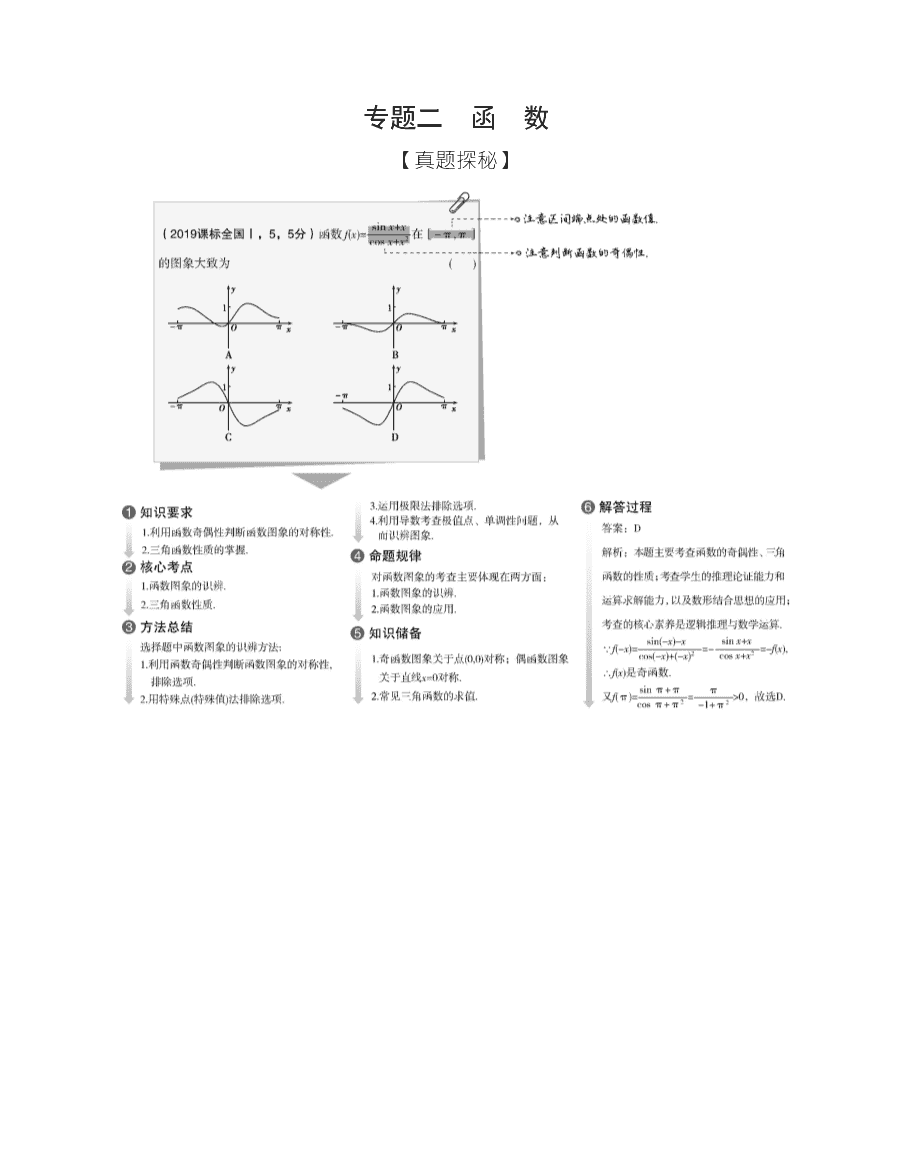
专题二　函　数 ‎【真题探秘】‎ ‎§2.1　函数的概念及表示 探考情 悟真题 ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 函数的概 念及表 示方法 了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念 ‎2016课标全国Ⅱ,10,5分 函数的定义域和值域 指数、对数的运算 ‎★★☆‎ ‎2015课标Ⅱ,13,5分 通过解析式求参数 ‎—‎ 分段 函数 了解简单的分段函数,并能简单应用(函数分段不超过三段)‎ ‎2018课标全国Ⅰ,12,5分 由分段函数解不等式 函数的图象 ‎★★☆‎ ‎2017课标全国Ⅲ,16,5分 根据分段函数解不等式 ‎—‎ ‎2015课标Ⅰ,10,5分 分段函数求值 解对数方程 分析解读 主要考查函数的有关概念、函数的三要素及表示方法.分段函数的应用是高考命题的热点,主要以选择题、填空题的形式出现.‎ 破考点 练考向 ‎【考点集训】‎ 考点一　函数的概念及表示方法 ‎　(2019黑龙江顶级名校联考,5)下列函数值域为R的是(　　)　 　　　　　　 　　　　　　 ‎ A.f(x)=‎1‎x+1‎ B.f(x)=ln x C.f(x)=cos 2x D.f(x)=sin x 答案　B　‎ 考点二　分段函数 ‎1.(2018河南洛阳期中,4)已知函数f(x)=‎2,x∈[0,1],‎x,x∉[0,1],‎若f(f(x))=2,则x的取值集合为(　　)‎ A.⌀ B.{x|0≤x≤1} C.{2} D.{x|x=2或0≤x≤1}‎ 答案　D　‎ ‎2.(2018江西南昌一模,8)设函数f(x)=‎2‎‎|x-a|‎‎,x≤1,‎x+1,x>1,‎若f(1)是f(x)的最小值,则实数a的取值范围为(　　)‎ A.[-1,2) B.[-1,0] C.[1,2] D.[1,+∞)‎ 答案　C　‎ ‎3.(2020届吉林第一中学调研,15)若函数f(x)=‎1‎‎2‎x-‎‎3‎‎2‎‎,x≤‎1‎‎2‎,‎logax(a>0,且a≠1),x>‎‎1‎‎2‎的值域是R,则实数a的取值范围是　　　　. ‎ 答案　‎‎2‎‎2‎‎,1‎ 炼技法 提能力 ‎【方法集训】‎ 方法1　函数定义域的求法 ‎1.(2019安徽蚌埠第一中学模拟,3)已知函数f(x)的定义域为(-2,2),则函数g(x)=fx‎3‎+f(x+1)的定义域为(　　)　　　　　 　　　　　　 　　　　　　 ‎ A.(-3,0) B.(-2,2) C.(-3,1) D.‎‎-‎1‎‎2‎,0‎ 答案　C　‎ ‎2.(2018衡水金卷信息卷(一),5)已知函数f(x)=x2-(2a-1)x-1(其中a>0,且a≠1)在区间‎1‎‎2‎‎,+∞‎上单调递增,则函数g(x)=‎1‎logax-1‎的定义域为(　　)‎ A.(-∞,a) B.(0,a) C.(0,a] D.(a,+∞)‎ 答案　B　‎ ‎3.(2020届甘肃甘谷第一中学检测,2)函数f(x)=‎3‎x‎2‎‎1-x+lg(3x+1)的定义域为(　　)‎ A.‎-‎1‎‎3‎,+∞‎ B.‎-‎1‎‎3‎,1‎ C.‎-‎1‎‎3‎,‎‎1‎‎3‎ D.‎‎-∞,-‎‎1‎‎3‎ 答案　B　‎ ‎4.(2018河南、河北重点高中联考,13)函数f(x)=‎4-‎‎4‎x+ln(x+4)的定义域为　　　　. ‎ 答案　(-4,1]‎ 方法2　求函数解析式的常用方法 ‎1.(2019山西晋中1月高考适应性考试,14)已知函数f(2x)=log2x+x,则f(4)=　　　　. ‎ 答案　3‎ ‎2.(2018广东东莞第二次综合考试,14)已知函数f(x)=ax-b(a>0), f(f(x))=4x-3,则f(2)=　　　　. ‎ 答案　3‎ ‎3.(2020届甘肃甘谷第一中学检测,13)已知f(ex)=‎1‎‎3‎x-1,则f(e)=　　　　. ‎ 答案　-‎‎2‎‎3‎ 方法3　分段函数问题的解题策略 ‎1.(2018河南商丘第二次模拟,3)设函数f(x)=x‎2‎‎-1(x≥2),‎log‎2‎x(00‎为奇函数,则f(g(2))=(　　)‎ A.-2 B.2 C.-1 D.1‎ 答案　B　‎ ‎【五年高考】‎ A组　统一命题·课标卷题组 考点一　函数的概念及表示方法 ‎1.(2016课标全国Ⅱ,10,5分)下列函数中,其定义域和值域分别与函数y=10lg x的定义域和值域相同的是(　　)‎ A.y=x B.y=lg x C.y=2x D.y=‎‎1‎x 答案　D　‎ ‎2.(2015课标Ⅱ,13,5分)已知函数f(x)=ax3-2x的图象过点(-1,4),则a=　　　　. ‎ 答案　-2‎ 考点二　分段函数 ‎1.(2018课标全国Ⅰ,12,5分)设函数f(x)=‎2‎‎-x‎,x≤0,‎‎1,x>0,‎则满足f(x+1)1,‎且f(a)=-3,则f(6-a)=(　　)‎ A.-‎7‎‎4‎ B.-‎5‎‎4‎ C.-‎3‎‎4‎ D.-‎‎1‎‎4‎ 答案　A　‎ ‎3.(2017课标全国Ⅲ,16,5分)设函数f(x)=x+1,x≤0,‎‎2‎x‎,x>0,‎则满足f(x)+f x-‎‎1‎‎2‎>1的x的取值范围是　　　　　　. ‎ 答案　‎‎-‎1‎‎4‎,+∞‎ B组　自主命题·省(区、市)卷题组 考点一　函数的概念及表示方法 ‎1.(2015重庆,3,5分)函数f(x)=log2(x2+2x-3)的定义域是(　　)　　　　　 　　　　　　 　　　　　　 ‎ A.[-3,1] B.(-3,1)‎ C.(-∞,-3]∪[1,+∞) D.(-∞,-3)∪(1,+∞)‎ 答案　D　‎ ‎2.(2018江苏,5,5分)函数f(x)=log‎2‎x-1‎的定义域为　　　　. ‎ 答案　[2,+∞)‎ ‎3.(2019江苏,4,5分)函数y=‎7+6x-‎x‎2‎的定义域是　　　　. ‎ 答案　[-1,7]‎ ‎4.(2016江苏,5,5分)函数y=‎3-2x-‎x‎2‎的定义域是　　　　. ‎ 答案　[-3,1]‎ 考点二　分段函数 ‎1.(2015湖北,7,5分)设x∈R,定义符号函数sgn x=‎1,x>0,‎‎0,x=0,‎‎-1,x<0.‎则(　　)‎ A.|x|=x|sgn x| B.|x|=xsgn|x|‎ C.|x|=|x|sgn x D.|x|=xsgn x 答案　D　‎ ‎2.(2015陕西,4,5分)设f(x)=‎1-x,x≥0,‎‎2‎x‎,x<0,‎则f(f(-2))=(　　)‎ A.-1 B.‎1‎‎4‎ C.‎1‎‎2‎ D.‎‎3‎‎2‎ 答案　C　‎ ‎3.(2015山东,10,5分)设函数f(x)=‎3x-b,x<1,‎‎2‎x‎,x≥1.‎若f f‎5‎‎6‎=4,则b=(　　)‎ A.1 B.‎7‎‎8‎ C.‎3‎‎4‎ D.‎‎1‎‎2‎ 答案　D　‎ ‎4.(2018江苏,9,5分)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(-2,2]上,f(x)=cosπx‎2‎,01,‎则f(f(-2))=　　　　, f(x)的最小值是　　　　. ‎ 答案　-‎1‎‎2‎;2‎6‎-6‎ C组　教师专用题组 考点一　函数的概念及表示方法 ‎1.(2014山东,3,5分)函数f(x)=‎1‎log‎2‎x-1‎的定义域为(　　)　　　　 　　　　　　 　　　　　　 ‎ A.(0,2) B.(0,2] C.(2,+∞) D.[2,+∞)‎ 答案　C　‎ ‎2.(2013陕西,10,5分)设[x]表示不大于x的最大整数,则对任意实数x,有(　　)‎ A.[-x]=-[x] B.x+‎‎1‎‎2‎=[x]‎ C.[2x]=2[x] D.[x]+x+‎‎1‎‎2‎=[2x]‎ 答案　D　‎ ‎3.(2013广东,2,5分)函数y=lg(x+1)‎x-1‎的定义域是(　　)‎ A.(-1,+∞) B.[-1,+∞)‎ C.(-1,1)∪(1,+∞) D.[-1,1)∪(1,+∞)‎ 答案　C　‎ ‎4.(2013安徽,11,5分)函数y=ln‎1+‎‎1‎x+‎1-‎x‎2‎的定义域为　　　　. ‎ 答案　(0,1]‎ ‎5.(2013浙江,11,4分)已知函数f(x)=x-1‎.若f(a)=3,则实数a=　　　　. ‎ 答案　10‎ ‎6.(2013安徽,14,5分)定义在R上的函数f(x)满足f(x+1)=2f(x).若当0≤x≤1时, f(x)=x(1-x),则当-1≤x≤0时, f(x)=　　　　　　. ‎ 答案　-‎1‎‎2‎x2-‎1‎‎2‎x 考点二　分段函数 ‎1.(2014江西,4,5分)已知函数f(x)=a·‎2‎x,x≥0,‎‎2‎‎-x‎,x<0‎(a∈R),若f [f(-1)]=1,则a=(　　)‎ A.‎1‎‎4‎ B.‎1‎‎2‎ C.1 D.2‎ 答案　A　‎ ‎2.(2017山东,9,5分)设f(x)=x‎,03‎(a>0且a≠1),若f(x)有最小值,则实数a的取值范围是(　　)‎ A.‎0,‎‎5‎‎6‎ B.‎1,‎‎5‎‎4‎ C.‎0,‎‎5‎‎6‎∪‎1,‎‎5‎‎4‎ D.(0,1)∪‎‎5‎‎4‎‎,+∞‎ 答案　C　‎ ‎4.(2018河南八市第一次测评,8)设函数f(x)=‎-x+λ,x<1(λ∈R),‎‎2‎x‎,x≥1,‎若对任意的a∈R,都有f(f(a))=2f(a)成立,则λ的取值范围是(　　)‎ A.(0,2] B.[0,2] C.[2,+∞) D.(-∞,2)‎ 答案　C　‎ ‎5.(2019河南郑州第二次质量检测,7)高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”如下:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数.例如:[-2.1]=-3,[3.1]=3,已知函数f(x)=‎2‎x‎+3‎‎2‎x‎+1‎,则函数y=[f(x)]的值域为(　　)‎ A.{0,1,2,3} B.{0,1,2} C.{1,2,3} D.{1,2}‎ 答案　D　‎ 二、填空题(每小题5分,共15分)‎ ‎6.(2020届甘肃甘谷第一中学检测,15)用min{a,b,c}表示a,b,c三个数中的最小值,设f(x)=min{2x,x+2,10-x}(x≥0),则f(x)的最大值为　　　　. ‎ 答案　6‎ ‎7.(2018河南南阳第一中学第二次考试,16)已知f(1-cos x)=sin2x,则f(x2)的解析式为　 . ‎ 答案　f(x2)=-x4+2x2,x∈[-‎2‎,‎2‎]‎ ‎8.(2019安徽第二次联考,16)若f(x)+3f‎1‎x=x+‎3‎x-2log2x对x∈(0,+∞)恒成立,且存在x0∈[2,4],使得f(x0)>m成立,则m的取值范围为　　　　. ‎ 答案　(-∞,6)‎