2019届二轮复习三角大题课件（33张）（全国通用）

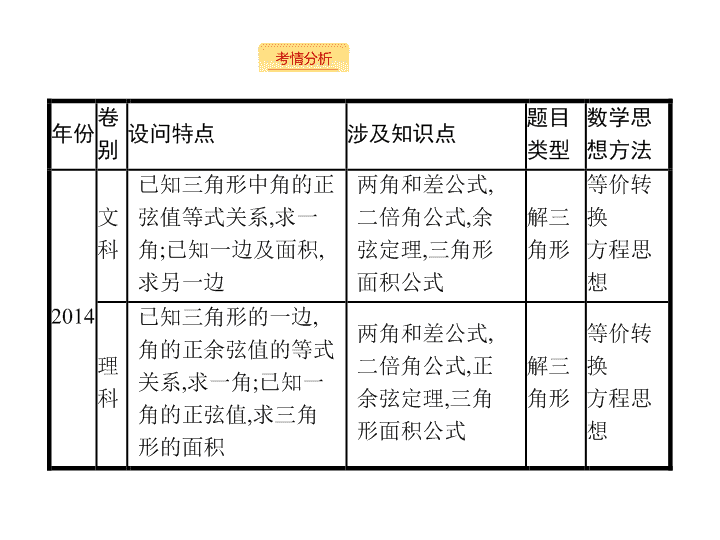
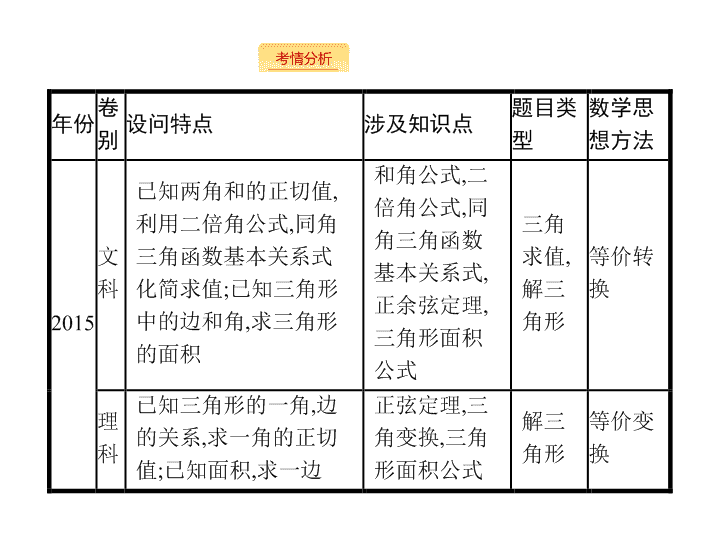
2019届二轮复习三角大题课件（33张）（全国通用）

2.3 　三角大题 - 2 - - 3 - - 4 - - 5 - - 6 - 1 . 正弦 ( 或余弦 ) 型函数 y=A sin( ω x+ φ )( 或 y=A cos( ω x+ φ )) 的对称中心是函数图象与 x 轴的交点 , 对称轴是过函数图象的最高点或者最低点且与 x 轴垂直的直线 ; 正切型函数 y=A tan( ω x+ φ ) 的图象是中心对称图形 , 不是轴对称图形 . 2 . 三角函数恒等变换 “ 四大策略 ” (1) 常值代换 : 特别是 “1” 的代换 ,1 = sin 2 θ + cos 2 θ = tan 45 ° 等 . (2) 角的配凑 : 如 α = ( α + β ) - β ,2 α = ( α + β ) + ( α - β ); α = [( α + β ) + ( α - β )] . (3) 降次与升次 : 正用二倍角公式升次 , 逆用二倍角公式降次 . (4) 弦、切互化 : 一般是切化弦 . - 7 - 3 . 解三角形的公式 变形 4 . 用余弦定理判断三角形的形状 : 当 b 2 +c 2 -a 2 > 0 时 , 可知 A 为锐角 ; 当 b 2 +c 2 -a 2 = 0 时 , 可知 A 为直角 ; 当 b 2 +c 2 -a 2 < 0 时 , 可知 A 为钝角 . 5 . 三个等价关系 : 在 △ ABC 中 , a , b , c 分别为 A , B , C 的对边 , 则 a>b ⇔ sin A> sin B ⇔ A>B. - 8 - 2.3.1 2.3.2 考向一 考 向二 2 . 3 . 1 　 三角函数与三角变换 三角函数式的化简与求 值 - 9 - 2.3.1 2.3.2 考向一 考 向二 - 10 - 2.3.1 2.3.2 考向一 考 向二 解题心得 化异为同法 : 解决三角函数化简与求值问题的总体思路就是化异为同 , 目的是消元减少未知量的个数 . 如把三角函数式中的异名、异角、异次化为同名、同角、同次 ; 如在三角函数求值中 , 把未知角用已知角表示 , 或把未知角通过三角变换化成已知角 ; 对于三角函数式中既有正弦、余弦函数又有正切函数 , 化简方法是切化弦 , 或者弦化切 , 目的是化异为同 . - 11 - 2.3.1 2.3.2 考向一 考 向二 - 12 - 2.3.1 2.3.2 考向一 考向二 - 13 - 2.3.1 2.3.2 考向一 考向二 解题心得 对于已知的三角函数是由多个三角函数式通过四则运算组合而成的 , 若求其函数的性质 , 一般的思路是通过三角变换 , 把多个三角函数式的代数和 ( 或积、商 ) 化成只有一项且只有一种名称的三角函数式 , 化简中常用到辅助角 公式 - 14 - 2.3.1 2.3.2 考向一 考向二 - 15 - 2.3.1 2.3.2 考向一 考向二 - 16 - 2.3.1 2.3.2 考向一 考向二 - 17 - 2.3.1 2.3.2 考向一 考向二 解题心得 利用函数 y= sin x 的有关性质求三角函数 f ( x ) =A sin( ω x+ φ ) 的单调区间、对称轴方程及 φ 值大小的题目时 , 把 ω x+ φ 看作一个整体 , 整体代换函数 y= sin x 的相关性质 , 进而求出题目所要求的量 . - 18 - 2.3.1 2.3.2 考向一 考向二 对 点训练 3 (2018 浙江杭州二中 6 月模拟 ) 设函数 f ( x ) =A sin( ω x+ φ )( A> 0, ω > 0, | φ |< π ) 图象中相邻的最高点和最低点分别为 (1) 求函数 f ( x ) 的单调递减区间 ; (2) 若函数 f ( x ) 的图象向左平移 θ ( θ > 0) 个单位长度后关于点 ( - 1,0) 对称 , 求 θ 的最小值 . - 19 - 2.3.1 2.3.2 考向一 考向二 - 20 - 2.3.1 2.3.2 考向一 考 向二 考 向三 2 . 3 . 2 　 解三角形 正弦、余弦定理与三角形面积的综合 问题 - 21 - 2.3.1 2.3.2 考向一 考 向二 考 向三 - 22 - 2.3.1 2.3.2 考向一 考 向二 考 向三 解题心得 正弦定理和余弦定理是解三角形时用到的两个重要定理 , 其作用主要是将已知条件中的边角关系转化为纯边或纯角的关系 , 使问题得以解决 . - 23 - 2.3.1 2.3.2 考向一 考 向二 考 向三 对点训练 1 在 △ ABC 中 , 角 A , B , C 所对的边分别为 a , b , c , 且满足 2 a cos B= 2 c-b. (1) 求角 A ; - 24 - 2.3.1 2.3.2 考向一 考 向二 考 向三 例 2 已知在 △ ABC 中 , D 是 BC 上的点 , AD 平分 ∠ BAC , △ ABD 的面积是 △ ADC 面积的 2 倍 . - 25 - 2.3.1 2.3.2 考向一 考 向二 考 向三 在 △ ABD 和 △ ADC 中 , 由余弦定理知 AB 2 =AD 2 +BD 2 - 2 AD·BD cos ∠ ADB , ① AC 2 =AD 2 +DC 2 - 2 AD·DC cos ∠ ADC. ② 因为 cos ∠ ADB=- cos ∠ ADC , 所以 ① + 2 × ② 得 AB 2 + 2 AC 2 = 3 AD 2 +BD 2 + 2 DC 2 = 6 . 由 (1) 知 AB= 2 AC , 所以 AC= 1 . - 26 - 2.3.1 2.3.2 考向一 考 向二 考 向三 解题心得 对于在四边形中解三角形的问题或把一个三角形分为两个三角形来解三角形的问题 , 分别在两个三角形中列出方程 , 组成方程组 , 通过加减消元或者代入消元 , 求出所需要的量 ; 对于含有三角形中的多个量的已知等式 , 化简求不出结果 , 需要依据题意应用正弦、余弦定理再列出一个等式 , 由此组成方程组通过消元法求解 . - 27 - 2.3.1 2.3.2 考向一 考 向二 考 向三 对点训练 2 (2018 全国 Ⅰ , 理 17) 在平面四边形 ABCD 中 , ∠ ADC= 90 ° , ∠ A= 45 ° , AB= 2, BD= 5 . (1) 求 cos ∠ ADB ; (2) 若 DC= 2 , 求 BC. - 28 - 2.3.1 2.3.2 考向一 考向二 考 向三 正弦、余弦定理与三角变换的综合 例 3 (2017 天津 , 理 15) 在 △ ABC 中 , 内角 A , B , C 所对的边分别为 a , b , c , 已知 a>b , a= 5, c= 6,sin B = . (1) 求 b 和 sin A 的值 ; - 29 - 2.3.1 2.3.2 考向一 考向二 考 向三 解题心得 三角形有三条边三个角共六个元素 , 知道其中三个 ( 其中至少知道一条边 ), 可求另外三个 ; 若题目要求的量是含三角形内角及常数的某种三角函数值 , 在解题时往往先通过正、余弦求出内角的三角函数值再应用和角公式及倍角公式通过三角变换求得结果 . - 30 - 2.3.1 2.3.2 考向一 考向二 考 向三 - 31 - 2.3.1 2.3.2 考向一 考 向二 考向三 正弦、余弦定理与三角变换及三角形面积的综合 例 4 (2018 浙江金华十校 4 月模拟 ) 在 △ ABC 中 , 角 A , B , C 所对的边为 a , b , c , 已知 sin A= sin( B-C ) + 2sin 2 B , B ≠ . (1) 求证 : c= 2 b ; (2) 若 △ ABC 的面积 S= 5 b 2 -a 2 , 求 tan A 的值 . (1) 证明 由 sin A= sin( B-C ) + 2sin 2 B , 得 sin( B+C ) = sin( B-C ) + 4sin B cos B , 展开化简得 ,cos B sin C= 2sin B cos B , 又因为 B ≠ , 所以 sin C= 2sin B , 则由正弦定理得 , c= 2 b. (2) 解 : 因为 △ ABC 的面积 S= 5 b 2 -a 2 , 所以 bc sin A= 5 b 2 -a 2 , 由 (1) 知 c= 2 b , 代入上式得 b 2 sin A= 5 b 2 -a 2 , ① 又由余弦定理得 a 2 =b 2 +c 2 - 2 bc cos A= 5 b 2 - 4 b 2 cos A , 代入 ① 得 b 2 sin A= 4 b 2 cos A , ∴ tan A= 4 . - 32 - 2.3.1 2.3.2 考向一 考 向二 考向三 解题心得 在解三角形中 , 若已知条件是由三角形的边及角的正弦、余弦函数构成时 , 解题方法通常是通过正弦定理、余弦定理把边转化成角的正弦 , 使已知条件变成了纯粹的角的正弦、余弦函数关系 , 这样既实现了消元的目的 , 又可利用三角变换化简已知条件 . - 33 - 2.3.1 2.3.2 考向一 考 向二 考向三 对点训练 4 (2017 全国 Ⅰ , 理 17) △ ABC 的内角 A , B , C 的对边分别为 a , b , c. 已知 △ ABC 的面积为 ( 1) 求 sin B sin C ; (2) 若 6cos B cos C= 1, a= 3, 求 △ ABC 的周长 .