高考物理一轮复习配套单元检测第五章 第4单元 课下综合提升

高考物理一轮复习配套单元检测第五章 第4单元 课下综合提升

‎1．一根长为L、质量为m的均匀链条放在光滑的水平桌面上，其长度的一半悬于桌边，若要将悬着的部分拉回桌面，至少做功(　　)‎ A.mgL　　　　　　　　 B.mgL C．mgL D.mgL 解析：悬于桌边的链条质量为。将其拉上桌面，重心升高，故至少做功为mgL。选项A正确。‎ 答案：A ‎2.如图1所示，足够长的传送带以恒定速率顺时针运行，将一个物体轻轻放在传送带底端，第一阶段物体被加速到与传送带具有相同的速度，第二阶段与传送带相对静止，匀速运动到达传送带顶端。下列说法正确的是(　　)‎ 图1‎ A．第一阶段摩擦力对物体做正功，第二阶段摩擦力对物体不做功 B．第一阶段摩擦力对物体做的功等于第一阶段物体动能的增加 C．第一阶段物体和传送带间的摩擦生热等于第一阶段物体机械能的增加 D．物体从底端到顶端全过程机械能的增加等于全过程物体与传送带间的摩擦生热 解析：第一阶段为滑动摩擦力做功，第二阶段为静摩擦力做功，两个阶段摩擦力方向都跟物体运动方向相同，所以摩擦力都做正功，选项A错误；由功能关系可知，第一阶段摩擦力对物体做的功(除重力之外的力所做的功)等于物体机械能的增加，即ΔE＝W阻＝F阻l物，摩擦生热为Q＝F阻l相对，又由于l传送带＝vt，l物＝t，所以l物＝l相对＝l传送带，即Q＝ΔE，选项C正确，B错误。第二阶段没有摩擦生热，但物体的机械能继续增加，结合选项C可以判断选项D错误。‎ 答案：C ‎3.如图2所示为运动员在蹦床运动中完成某个动作的示意图，图中虚线PQ是弹性蹦床的原始位置，A为运动员抵达的最高点，B为运动员刚抵达蹦床时的位置，C为运动员抵达的最低点。不考虑空气阻力和运动员与蹦床作用时的机械能损失，在A、B、C三个位置上运动员的速度分别是vA、vB、vC，机械能分别是EA、EB、EC，则它们的大小关系是(　　)‎ 图2‎ A．vAvB，vBEC D．EA>EB，EB＝EC 解析：运动员在最高点A的速度为零，刚抵达B位置时的速度不为零，vAvC，故A、B错；以运动员为研究对象，B→A机械能守恒，EA＝EB，B→C弹力对运动员做负功，机械能减小，EB>EC，故C对，D错。‎ 答案：C ‎4．重物m系在上端固定的轻弹簧下端，用手托起重物，使弹簧处于竖直方向，弹簧的长度等于原长时，突然松手，重物下落的过程中，对于重物、弹簧和地球组成的系统来说，错误的是(弹簧始终在弹性限度内变化)(　　)‎ A．重物的动能最大时，重力势能和弹性势能的总和最小 B．重物的重力势能最小时，动能最大 C．弹簧的弹性势能最大时，重物的动能最小 D．重物的重力势能最小时，弹簧的弹性势能最大 解析：重物下落过程中，只发生动能、重力势能和弹性势能的相互转化，所以当动能最大时，重力势能和弹性势能的总和最小，A正确；当重物的重力势能最小时，重物应下落到最低点，其速度为零，动能最小，此时弹簧伸长量最大，弹性势能最大，故B错误，C、D正确。‎ 答案：B ‎5.如图3所示，质量m＝‎10 kg和M＝‎20 kg的两物块，叠放在光滑水平面上，其中物块m通过处于水平方向的轻弹簧与竖直墙壁相连，初始时刻，弹簧处于原长状态，弹簧的劲度系数k＝250 N/m。现用水平力F作用在物块M上，使其缓慢地向墙壁移动，当移动‎40 cm时，两物块间开始相对滑动，在相对滑动前的过程中，下列说法中正确的是(　　)‎ 图3‎ A．M受到的摩擦力保持不变 B．物块m受到的摩擦力对物块m不做功 C．推力做的功等于弹簧增加的弹性势能 D．开始相对滑动时，推力F的大小等于200 N 解析：取m和M为一整体，由平衡条件可得：F＝kx，隔离m，由平衡条件可得，Ff＝kx，可见M缓慢右移过程中，m对M的摩擦力在增大，开始滑动时 ，Ff＝kxm＝100 N，故此时推力F＝100 N，A、D均错误；m受到的摩擦力对m做正功，B错误；由能量守恒定律可知，推力F做的功全部转化为弹簧的弹性势能，C正确。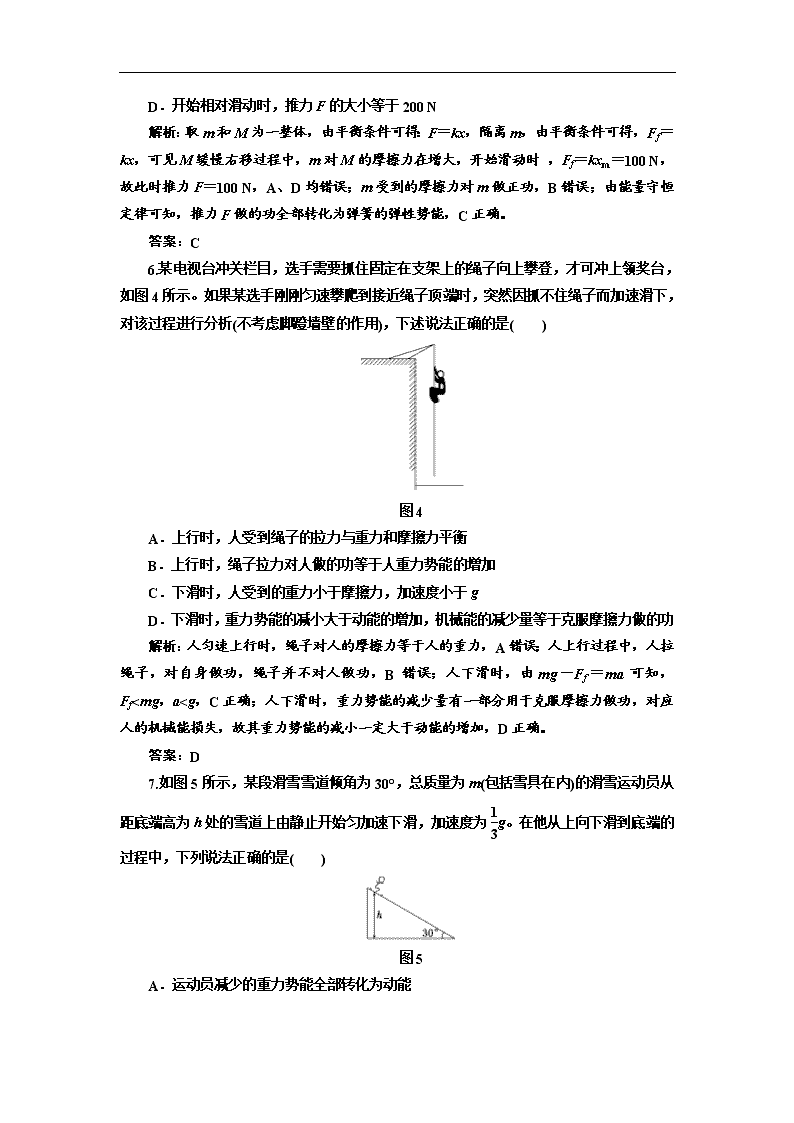‎ 答案：C ‎6.某电视台冲关栏目，选手需要抓住固定在支架上的绳子向上攀登，才可冲上领奖台，如图4所示。如果某选手刚刚匀速攀爬到接近绳子顶端时，突然因抓不住绳子而加速滑下，对该过程进行分析(不考虑脚蹬墙壁的作用)，下述说法正确的是(　　)‎ 图4‎ A．上行时，人受到绳子的拉力与重力和摩擦力平衡 B．上行时，绳子拉力对人做的功等于人重力势能的增加 C．下滑时，人受到的重力小于摩擦力，加速度小于g D．下滑时，重力势能的减小大于动能的增加，机械能的减少量等于克服摩擦力做的功 解析：人匀速上行时，绳子对人的摩擦力等于人的重力，A错误；人上行过程中，人拉绳子，对自身做功，绳子并不对人做功，B错误；人下滑时，由mg－Ff＝ma可知，FfFf＝μmg＝2 N。‎ 所以m、M相对滑动a＝＝μg＝‎2 m/s2。‎ ‎(2)速度最大时，弹簧伸长x，则kx＝μmg，‎ 所以x＝‎0.08 m，由功能关系 μmgx＝kx2＋mvm2。‎ 所以vm＝‎0.4 m/s。‎ 答案：(1)‎2 m/s2　(2)‎0.4 m/s ‎12．(2012·聊城模拟)一质量为M＝‎2 kg的小物块随足够长的水平传送带一起运动，被一水平向左飞来的子弹击中，子弹并从物块中穿过，如图10甲所示，地面观察者记录了小物块被击中后的速度随时间的变化关系，如图乙所示(图中取向右运动的方向为正方向)，已知传送带的速度保持不变，‎ ‎(1)指出传送带的速度v的方向及大小，说明理由。‎ ‎(2)计算物块与传送带间的动摩擦系数？‎ ‎(3)计算物块对传送带总共做了多少功？系统有多少能量转化为内能？‎ 图10‎ 解析：(1)由图可知，物块被击穿后先向左做匀减速运动，速度为零后，又向右做匀加速运动，当速度等于‎2 m/s以后随传送带一起匀速运动，所以传送带的速度方向向右，大小为‎2 m/s。‎ ‎(2)由图可知，a＝＝ m/s2＝‎2 m/s2‎ 由牛顿第二定律得滑动摩擦力Ff＝Ma，其中Ff＝μFN，‎ FN＝Mg，‎ 所以物块与传送带的动摩擦系数μ＝＝＝0.2‎ ‎(3)由图可知，传送带与物块存在摩擦力的时间只有3 s，传送带在这段时间内的位移x＝vt＝2×‎3 m＝‎‎6 m 所以物块对传送带所做的功为 W＝－Ffx＝－4×6 J＝－24 J 物块相对于传送带通过的路程x′＝t＝×‎3 m＝‎9 m，所以转化为内能EQ＝Ffx′＝4×9 J＝36 J。‎ 答案：(1)向右　‎2 m/s　理由见解析　(2)0.2‎ ‎(3)－24 J　36 J