人教版必修二7.5《宇宙航行》WORD教案1

人教版必修二7.5《宇宙航行》WORD教案1

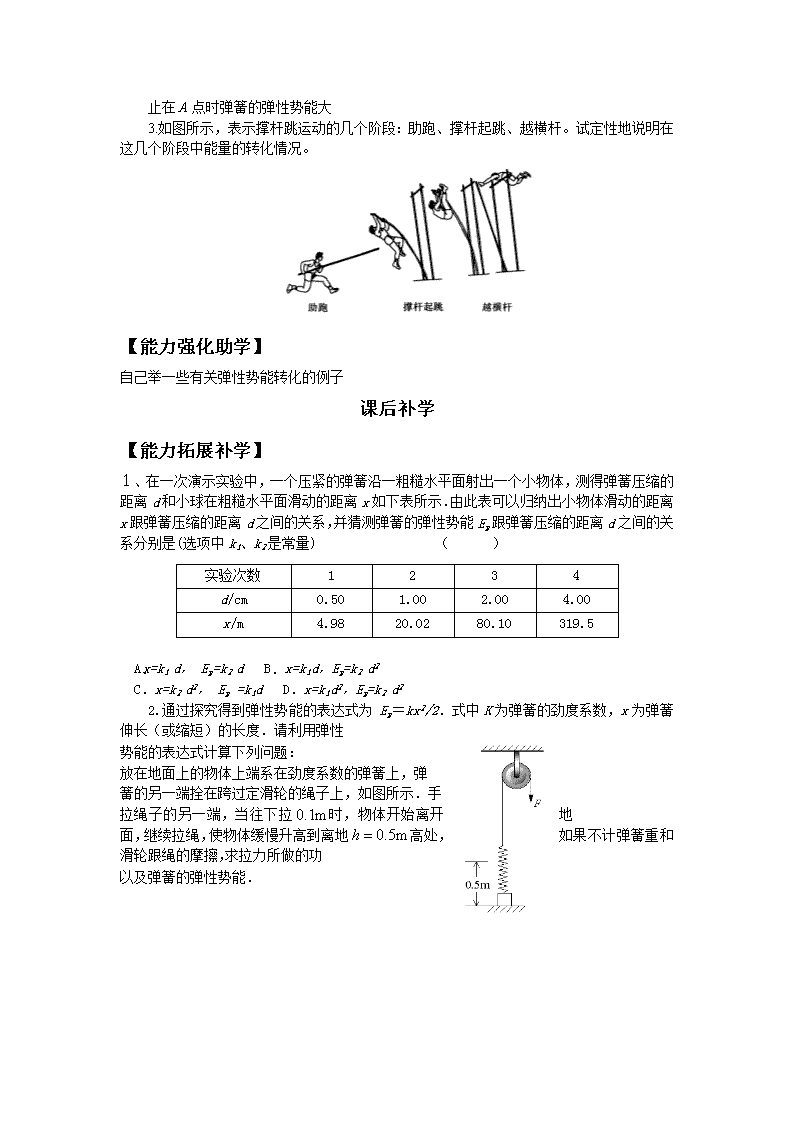
☆ ‎☆☆“四学”教学模式之物理科教学设计☆☆☆‎ 探究弹性势能的表达式—郑维刚、武士元 课尾导学 ‎【学习目标】‎ ‎1、理解弹性势能的概念，会分析决定弹簧弹性势能大小的相关因素。‎ ‎2、知道探究弹性势能表达式的思路。‎ ‎3、体会探究过程中的猜想、类比、迁移、分析、和转化的方法。‎ ‎4、领悟求弹力做功时通过细分过程化变力为恒力的思想方法。‎ 学习方法指导：‎ a）类比方法确定弹力做功 课前自学 ‎【基础知识自学】‎ 一． 弹性势能 ‎1. 弹性形变： ，试举出常见的弹性形变的例子： 。‎ ‎2.势能的概念： 。‎ ‎3.弹性势能： 。‎ 二．探究弹性势能的表达式 ‎1.有关因素 ‎ ‎⑴在弹簧的弹性限度内，弹簧的弹力与弹簧的伸长量之间的关系为：F= 。‎ ‎⑵类比重力势能，重力势能大小与物体的重力和高度有关，那么弹性势能就有可能与 和 有关。‎ ‎⑶事实验证 ‎ 对同一根弹簧，压缩不同的长度，将木块弹出的距离 ，说明弹簧弹性势能与 有关。 ‎ 对不同的弹簧，压缩相同的长度，将木块弹出的距离 ，说明弹簧弹性势能与 有关。‎ ‎2.弹性势能与拉力做功的关系 ‎⑴方法 类比重力做功与重力势能变化的关系 ‎⑵弹力做正功，弹性势能 ‎ ‎⑶弹力做负功，弹性势能 ‎ ‎⑷弹力做功多少与弹性势能变化量的关系 。‎ ‎3.怎样计算拉力做的功？‎ 重力是恒力，重力做功等于重力与物体在竖直方向移动距离的乘积。那么，拉伸弹簧时，拉力做功该怎样计算？‎ ‎4.怎样计算求和式？‎ ‎⑴方法：类比速度——时间图像中求位移的方法 ‎⑵怎样计算拉力做功的求和式？是否可以用F-l图象下一个梯形的面积来代表功？‎ ‎⑶拉力做功的表达式 。‎ ‎【基本规律自学】‎ 弹性势能表达式的得出和弹性势能与其他能量的转化 ‎1．弹簧的弹性势能与下列哪些因素有关（ ）‎ A．弹簧的长度 B．弹簧的劲度系数 C．弹簧的形变量 D．弹簧的原长 ‎2．讨论弹性势能，要从下述哪个问题的分析入手（ ）‎ A．重力做功 B．弹力做功 C．弹簧的劲度系数 D．弹簧的形变量 ‎3．弹簧的一端固定，处于自然长度．现对弹簧的另一端施加一个拉力，如图2示，关于拉力做功（或弹簧克服拉力做功）与弹性势能变化的关系，以下说法中正确的是（ ）‎ 图2‎ F A．拉力对弹簧做正功，弹簧的弹性势能增加 B．拉力对弹簧做正功，弹簧的弹性势能减少 C．弹簧克服拉力做功，弹簧的弹性势能增加 D．弹簧克服拉力做功，弹簧的弹性势能减少 ‎4．在一次“蹦极”运动中，人由高空落下，到最低点的整个过程中，下列说法中正确的是（ ）‎ A．重力对人做正功 B．人的重力势能减小了 ‎ C．橡皮绳对人做负功 D．橡皮绳的弹性势能增加了 ‎5．两弹簧的劲度系数之比为1:2，在弹性限度内的形变量之比为2:1，则它们的弹性势能之比为（ ）‎ A． 1:2   B． 2:‎1 ‎   C． 1:4   D． 4:1‎ ‎6．一根弹簧的劲度系数为k＝1000N/m，在弹性限度内，它压缩‎5cm，则贮存的弹性势能为 ，若拉伸‎5cm，贮存的弹性势能为 ．‎ ‎【自学质疑感悟】‎ ‎ ‎ 课上助学 ‎【自学学情反馈】‎ 小组合作检查学案完成情况。‎ ‎【能力提升助学】‎ ‎1.在猜想弹性势能可能与哪几个物体量有关的时候，有人猜想弹性势能与弹簧的劲度系数k与弹簧的伸长量x有关，但究竟是与x的一次方，还是x但二次方，还是x的三次方有关呢？请完成下面练习以助思考．（1J＝1N·m）‎ ‎（1）若弹性势能Ep∝kx，由于劲度系数k的单位是N/m，弹簧伸长量x的单位是m，则kx的单位是 ．‎ ‎（2）若弹性势能Ep∝kx2，由于劲度系数k的单位是N/m，弹簧伸长量x的单位是m，则kx2的单位是 ．‎ ‎（3）若弹性势能Ep∝kx3，由于劲度系数k的单位是N/m，弹簧伸长量x的单位是m，则kx3的单位是 ．‎ ‎ 从以上对单位的计算，你可以得到什么启示？ ‎ ‎2.一竖直弹簧下端固定于水平地面上，小球从弹簧的正 上方高为h的地方自由下落到弹簧上端，如图所示，经 几次反弹以后小球最终在弹簧上静止于某一点A处，‎ 则（ ）‎ A．h愈大，弹簧在A点的压缩量愈大 B．弹簧在A点的压缩量与h无关 C．h愈大，最终小球静止在A点时弹簧的弹性势能愈大 D．小球第一次到达A点时弹簧的弹性势能比最终小球静 止在A点时弹簧的弹性势能大 ‎3.如图所示，表示撑杆跳运动的几个阶段：助跑、撑杆起跳、越横杆。试定性地说明在这几个阶段中能量的转化情况。‎ ‎【能力强化助学】‎ 自己举一些有关弹性势能转化的例子 课后补学 ‎【能力拓展补学】‎ ‎１、在一次演示实验中，一个压紧的弹簧沿一粗糙水平面射出一个小物体，测得弹簧压缩的距离d和小球在粗糙水平面滑动的距离x如下表所示．由此表可以归纳出小物体滑动的距离x跟弹簧压缩的距离d之间的关系，并猜测弹簧的弹性势能Ep跟弹簧压缩的距离d之间的关系分别是(选项中k1、k2是常量) （ ）‎ 实验次数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ d/cm ‎0.50‎ ‎1.00‎ ‎2.00‎ ‎4.00‎ x/m ‎4.98‎ ‎20.02‎ ‎80.10‎ ‎319.5‎ A．x=k1 d， Ep=k2 d B．x=k1d，Ep=k2 d2 ‎ C．x=k2 d2， Ep =k1d D．x=k1d2，Ep=k2 d2‎ ‎2.通过探究得到弹性势能的表达式为 Ep＝kx2/2．式中K为弹簧的劲度系数，x为弹簧伸长（或缩短）的长度．请利用弹性 势能的表达式计算下列问题：‎ 放在地面上的物体上端系在劲度系数的弹簧上，弹 簧的另一端拴在跨过定滑轮的绳子上，如图所示．手 拉绳子的另一端，当往下拉时，物体开始离开地 面，继续拉绳，使物体缓慢升高到离地高处，如果不计弹簧重和滑轮跟绳的摩擦，求拉力所做的功 以及弹簧的弹性势能． ‎ ‎【能力建构补学】‎ 教师指导建构 请根据本节课所学内容列出本节课的结构提纲。‎ 学生自主建构 请将本节课你的学习心得写出来