【物理】2020届二轮复习专题十选考部分学案
专题十 选考部分
要点提炼
1.热学基本概念和规律
(1)分子动理论与内能
①分子动理论
a.物体是由大量分子组成的:油膜法测分子直径d=。
b.分子的热运动:分子永不停息的无规则运动。证据:扩散现象、布朗运动。
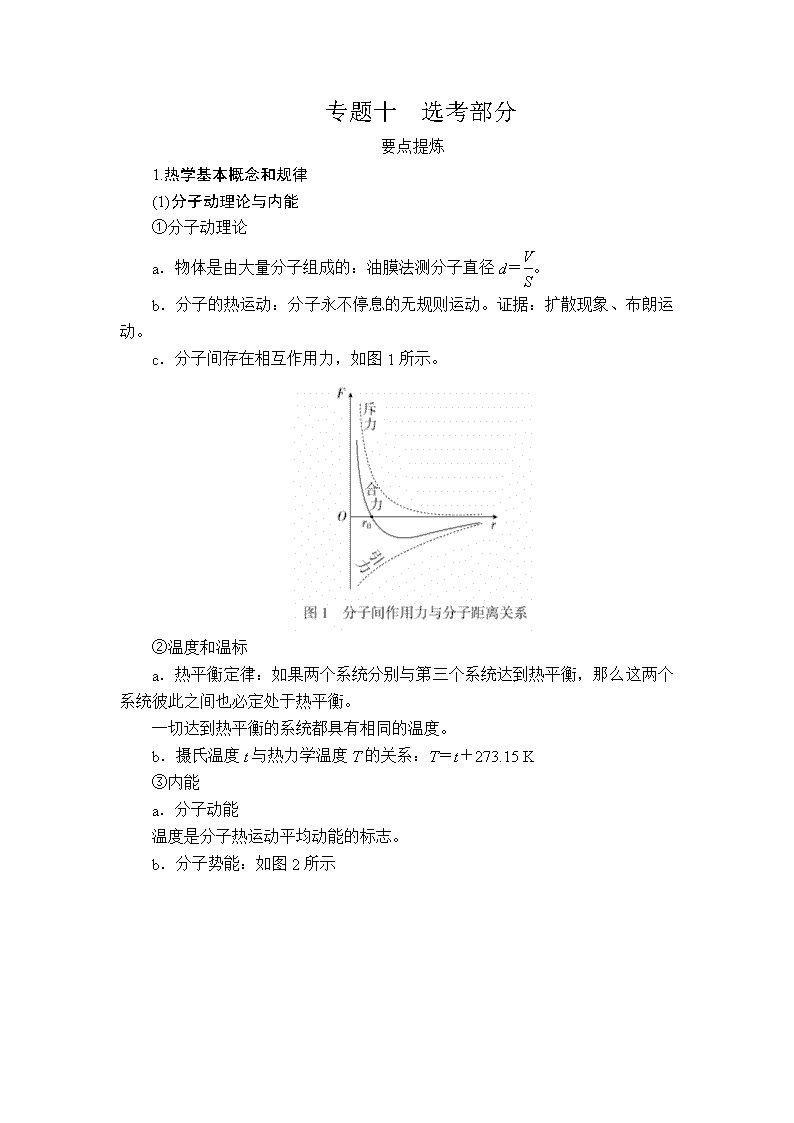
c.分子间存在相互作用力,如图1所示。
②温度和温标
a.热平衡定律:如果两个系统分别与第三个系统达到热平衡,那么这两个系统彼此之间也必定处于热平衡。
一切达到热平衡的系统都具有相同的温度。
b.摄氏温度t与热力学温度T的关系:T=t+273.15 K
③内能
a.分子动能
温度是分子热运动平均动能的标志。
b.分子势能:如图2所示
c.内能:是对于物体而言。物体中所有分子的热运动动能与分子势能的总和,叫做物体的内能。
(2)气体状态方程
①玻意耳定律(等温):p1V1=p2V2。
②查理定律(等容):=。
③盖—吕萨克定律(等压):=。
④理想气体状态方程:=。
(3)固体、液体、液晶
①固体
a.晶体
形状规则,有固定熔点。
单晶体:各向异性的性质;多晶体:各向同性。
有的物质在不同条件下能够生成不同的晶体。那是因为组成它们的微粒能够按照不同规则在空间分布。例如均由碳原子组成的石墨和金刚石。
b.非晶体
无确定几何形状,物理性质各向同性,无固定熔点。
同种物质也可能以晶体和非晶体两种不同的形态出现。物质是晶体还是非晶体,并不是绝对的,是能够相互转化的,例如天然水晶和石英玻璃。
②液体
a.表面张力:使液体表面积收缩到最小。
b.浸润和不浸润:是分子力作用的表现。一种液体是否浸润某种固体,与这两种物质的性质都有关系。如图3所示。
水可以浸润玻璃,但水不能浸润蜂蜡和石蜡;水银不浸润玻璃,但水银浸润铅。
c.毛细现象:浸润液体在细管中上升的现象,以及不浸润液体在细管中下降的现象。
d.液晶:具有液体的流动性;具有晶体的光学各向异性。
e.饱和汽与饱和气压
饱和汽:与液体处于动态平衡的蒸汽。
饱和气压:在一定温度下,饱和汽的压强。随温度而变。
绝对湿度:用空气中所含水蒸气的压强p1来表示。
相对湿度:空气中水蒸气的压强与同一温度时水的饱和气压的比值。
相对湿度=
(4)热力学定律
①热力学第一定律:ΔU=Q+W。
②热力学第二定律
a.不可能使热量由低温物体传递到高温物体,而不引起其他变化。
b.不可能从单一热源吸收热量并把它全部用来对外做功,而不引起其他变化。
2.气体压强的几种求法
(1)参考液片法:选取假想的液体薄片(自身重力不计)为研究对象,分析液片两侧受力情况,建立平衡方程,消去面积,得到液片两侧压强相等方程,求得气体的压强。
(2)力平衡法:
选与气体接触的液柱(或活塞)为研究对象进行受力分析,得到液柱(或活塞)的受力平衡方程,求得气体的压强。
(3)等压面法:在连通器中,同一种液体(中间不间断)同一深度处压强相等。
(4)牛顿第二定律法:求解加速运动系统中封闭气体压强,通常选与气体接触的液柱或活塞为研究对象,进行受力分析,利用牛顿第二定律列方程求解。
3.机械振动与机械波的有关公式
(1)简谐运动的方程x=Acos(ωt+φ)。
(2)单摆周期公式T=2π。
(3)波长、波速和周期(或频率)的关系式λ=vT=。
4.光的折射和全反射的有关公式
(1)n=(θ1、θ2分别为空气到介质时的入射角和折射角)。
(2)n=(c、v分别为光在真空、介质中的速度)。
(3)临界角公式:sinC=。
5.折射率与频率(或波长)的关系:在同一介质中,不同频率的光对应的折射率不同,频率越高,波长越短,对应的折射率越大。
6.光的双缝干涉间距:Δx=λ。
高考考向1 气体实验定律的应用
命题角度1 汽缸活塞类问题
例1 (2019·全国卷Ⅰ)热等静压设备广泛应用于材料加工中。该设备工作时,先在室温下把惰性气体用压缩机压入到一个预抽真空的炉腔中,然后炉腔升温,利用高温高气压环境对放入炉腔中的材料加工处理,改善其性能。一台热等静压设备的炉腔中某次放入固体材料后剩余的容积为0.13 m3,炉腔抽真空后,在室温下用压缩机将10瓶氩气压入到炉腔中。已知每瓶氩气的容积为3.2×10-2 m3,使用前瓶中气体压强为1.5×107 Pa,使用后瓶中剩余气体压强为2.0×106 Pa;室温温度为27 ℃。氩气可视为理想气体。
(1)求压入氩气后炉腔中气体在室温下的压强;
(2)将压入氩气后的炉腔加热到1227 ℃,求此时炉腔中气体的压强。
解析 (1)设初始时每瓶气体的体积为V0,压强为p0;使用后气瓶中剩余气体的压强为p1。假设体积为V0、压强为p0的气体压强变为p1时,其体积膨胀为V1。由玻意耳定律
p0V0=p1V1①
被压入进炉腔的气体在室温和p1条件下的体积为
V1′=V1-V0②
设10瓶气体压入完成后炉腔中气体的压强为p2,体积为V2。由玻意耳定律
p2V2=10p1V1′ ③
联立①②③式并代入题给数据得
p2=3.2×107 Pa④
(2)设加热前炉腔的温度为T0,加热后炉腔温度为T1,气体压强为p3,由查理定律
=⑤
联立④⑤式并代入题给数据得
p3=1.6×108 Pa⑥
答案 (1)3.2×107 Pa (2)1.6×108 Pa
(1)气体问题中汽缸活塞类模型的处理思路
①弄清题意,确定研究对象。一般地说,研究对象分为两类:一类是热学研究对象(一定质量的理想气体);另一类是力学研究对象(汽缸、活塞等)。
②分析清楚题目所述的物理过程。对热学研究对象分析清楚初、末状态及状态变化过程,依据气体实验定律或理想气体状态方程=恒量,列出式子;对力学研究对象要正确地进行受力分析,依据力学规律列出方程。
③注意挖掘题目中的隐含条件,如几何关系等,列出辅助方程。
④多个方程联立求解。对求解的结果注意检验它们的合理性。
(2)在“充气、抽气”模型中可以假设把充进或抽出的气体包含在气体变化的始末状态中,即用等效法把变质量问题转化为恒定质量的问题。
①充气中的变质量问题
设想将充进容器内的气体用一个无形的弹性口袋收集起来,那么当我们取容器和口袋内的全部气体作为研究对象时,这些气体状态不管怎样变化,其质量总是不变的。这样,就将变质量的问题转化成质量一定的问题了。
②抽气中的变质量问题
用抽气筒对容器抽气的过程中,对每一次抽气而言,气体质量发生变化,其解决方法和充气问题类似,取剩余气体和抽出的气体作为研究对象,这些气体不管怎样变化,其质量总是不变的。
备课记录:
1.(2019·全国卷Ⅱ)如图,一容器由横截面积分别为2S和S的两个汽缸连通而成,容器平放在水平地面上,汽缸内壁光滑。整个容器被通过刚性杆连接的两活塞分隔成三部分,分别充有氢气、空气和氮气。平衡时,氮气的压强和体积分别为p0和V0,氢气的体积为2V0,空气的压强为p。现缓慢地将中部的空气全部抽出,抽气过程中氢气和氮气的温度保持不变,活塞没有到达两汽缸的连接处,求
(1)抽气前氢气的压强;
(2)抽气后氢气的压强和体积。
答案 (1)(p0+p) (2)p0+p
解析 (1)设抽气前氢气的压强为p10,根据力的平衡条件得
p10·2S+p·S=p·2S+p0·S①
得p10=(p0+p)②
(2)设抽气后氢气的压强和体积分别为p1和V1,氮气的压强和体积分别为p2和V2。根据力的平衡条件有
p2·S=p1·2S③
由玻意耳定律得
p1V1=p10·2V0④
p2V2=p0V0⑤
由于两活塞用刚性杆连接,故
V1-2V0=2(V0-V2)⑥
联立②③④⑤⑥式解得
p1=p0+p
V1=。
命题角度2 液柱类问题
例2 (2019·全国卷Ⅲ)如图,一粗细均匀的细管开口向上竖直放置,管内有一段高度为2.0 cm的水银柱,水银柱下密封了一定量的理想气体,水银柱上表面到管口的距离为2.0 cm。若将细管倒置,水银柱下表面恰好位于管口处,且无水银滴落,管内气体温度与环境温度相同。已知大气压强为76 cmHg,环境温度为296 K。
(1)求细管的长度;
(2)若在倒置前,缓慢加热管内被密封的气体,直到水银柱的上表面恰好与管口平齐为止,求此时密封气体的温度。
解析 (1)设细管的长度为L,横截面的面积为S,水银柱高度为h;初始时,设水银柱上表面到管口的距离为h1,被密封气体的体积为V,压强为p;细管倒置时,被密封气体的体积为V1,压强为p1。由玻意耳定律有
pV=p1V1①
由力的平衡条件有
pS=p0S+ρghS②
p1S+ρghS=p0S③
式中,ρ、g分别为水银的密度和重力加速度的大小,p0为大气压强。由题意有
V=S(L-h1-h)④
V1=S(L-h)⑤
由①②③④⑤式和题给数据得
L=41 cm⑥
(2)设气体被加热前后的温度分别为T0和T,由盖—吕萨克定律有=⑦
由④⑤⑥⑦式和题给数据得T=312 K。
答案 (1)41 cm (2)312 K
气体实验定律与热力学定律问题的处理思路
备课记录:
2. (2019·河南省八市三模)如图所示,粗细均匀的U形管中,封闭了两段水银柱和两部分空气柱,水银柱A的长度h1=25 cm,位于左侧封闭端的顶部。水银柱B与A之间的空气柱长度L1=12.5 cm,右侧被活塞C封闭的空气柱长度L2=12.5 cm,已知玻璃管周围环境温度t=27 ℃时,右侧封闭空气柱的压强恰为p0=75 cmHg,水银柱B左右两部分液面的高度差h2=45 cm。保持环境温度t=27 ℃不变,缓慢拉动活塞C,求:
(1)当水银柱A恰好对U形管的顶部没有压力时,右侧封闭气体的压强为多少?
(2)当U形管内B部分的水银面相平时,活塞C共向上移动多少?
答案 (1)65 cmHg (2)47.5 cm
解析 (1)左侧气体做等温变化,有:
p1SL1=p1′SL1′
p1=p0-ρgh2=30 cmHg,p1′=25 cmHg
解得:L1′=15 cm
故水银柱B左右两部分液面的高度差变为
h2′=h2-2(L1′-L1)=40 cm
右侧气体压强为
p2′=p1′+ρgh2′=65 cmHg。
(2)B部分的水银面相平时,左侧液面下降,右侧液面上升
水银柱A下降,左侧气体压强仍为p1′=25 cmHg
此时左右两侧气体压强相等,即右侧气体压强p″=25 cmHg
右侧气柱做等温变化,有:p0SL2=p″SL2″
解得:L2″=37.5 cm;
则活塞上升的高度h=L2″-L2+=47.5 cm。
高考考向2 气体实验定律与图象、热力学第一定律综合应用
例3 (2019·全国卷Ⅱ)如pV图所示,1、2、3三个点代表某容器中一定量理想气体的三个不同状态,对应的温度分别是T1、T2、T3。用N1、N2、N3分别表示这三个状态下气体分子在单位时间内撞击容器壁上单位面积的平均次数,则N1________N2,T1________T3,N2________N3。(填“大于”“小于”或“等于”)
解析 根据理想气体状态方程有==,可知T1>T2,T2
T2,所以状态1时气体分子热运动的平均动能大,热运动的平均速率大,体积相等,分子数密度相等,故分子在单位时间内对单位面积容器壁的平均碰撞次数多,即N1>N2;对于状态2、3,由于T2N3。
答案 大于 等于 大于
近3年全国高考热学部分对气体实验定律与图象、热力学第一定律、分子动理论(气体温度、压强的微观意义)等的综合考查比较多,也是一个难点。另外2019全国卷Ⅰ考过与密度相关的综合问题,2017全国卷Ⅱ考过与密度、浮力相关的综合问题。对于这类问题:
(1)首先要熟练掌握理想气体状态方程和热力学第一定律方程的运用;
(2)如果题目涉及图象,要先弄清是pV图象、pT图象还是VT图象,并根据气体状态变化的图线结合理想气体状态方程分析第三个量的变化情况,然后结合热力学第一定律分析吸放热和内能变化情况;
(3)与气体有关的分子动理论(包括气体分子速率分布、气体温度和内能、气体压强)前几年基本是考查对知识的简单理解,2019年全国卷Ⅱ考查对这部分知识的理解运用,难度较大。其中气体压强的微观意义是个难点,应抓住教材,加深理解。由教材可知,气体压强的影响因素:①从气体压强产生的原理角度:单位时间撞击到容器壁单位面积上的分子数N,每个分子对容器壁的平均撞击力;②从气体微观状态量角度:气体的分子数密度n,气体分子平均动能k。注意N和n是不同的物理量(参见例题)。
备课记录:
3-1 (2019·全国卷Ⅰ)某容器中的空气被光滑活塞封住,容器和活塞绝热性能良好,空气可视为理想气体。初始时容器中空气的温度与外界相同,压强大于外界。现使活塞缓慢移动,直至容器中的空气压强与外界相同。此时,容器中空气的温度________(填“高于”“低于”或“等于”)外界温度,容器中空气的密度________(填“大于”“小于”或“等于”)外界空气的密度。
答案 低于 大于
解析 活塞光滑,容器绝热,容器内空气体积增大,对外做功,由ΔU=W+Q知,气体内能减少,温度降低。
气体的压强与温度和单位体积内的分子数有关,由于容器内空气的温度低于外界温度,但压强相同,则容器中空气的密度大于外界空气的密度。
3-2 (2018·全国卷Ⅰ)(多选)如图,一定质量的理想气体从状态a
开始,经历过程①、②、③、④到达状态e。对此气体,下列说法正确的是( )
A.过程①中气体的压强逐渐减小
B.过程②中气体对外界做正功
C.过程④中气体从外界吸收了热量
D.状态c、d的内能相等
E.状态d的压强比状态b的压强小
答案 BDE
解析 由理想气体状态方程=可知,体积不变温度升高即Tb>Ta,则pb>pa,即过程①中气体的压强逐渐增大,A错误;由于过程②中气体体积增大,所以过程②中气体对外做功,B正确;过程④中气体体积不变,对外做功为零,温度降低,内能减小,根据热力学第一定律,过程④中气体放出热量,C错误;由于状态c、d的温度相等,根据理想气体的内能只与温度有关,可知状态c、d的内能相等,D正确;由理想气体状态方程=C可得p=C,即TV图中的点与原点O的连线的斜率正比于该点的压强,故状态d的压强比状态b的压强小,E正确。
高考考向3 机械振动与机械波
例4 (2019·全国卷Ⅰ)(多选)一简谐横波沿x轴正方向传播,在t=时刻,该波的波形图如图a所示,P、Q是介质中的两个质点。图b表示介质中某质点的振动图象。下列说法正确的是( )
A.质点Q的振动图象与图b相同
B.在t=0时刻,质点P的速率比质点Q的大
C.在t=0时刻,质点P的加速度的大小比质点Q的大
D.平衡位置在坐标原点的质点的振动图象如图b所示
E.在t=0时刻,质点P与其平衡位置的距离比质点Q的大
解析 t=时刻,质点Q在平衡位置,向上振动,对应的振动图象与图b不符,A错误;t=0时刻的波形图如图所示(图a的波形图左移半个波长即可得到),质点P在最低点,质点Q在平衡位置,质点Q的速率比质点P的大,质点P的加速度大小比质点Q的大,质点P此时所在位置与其平衡位置的距离为振幅,质点Q在平衡位置,与其平衡位置的距离为0,故B错误,C、E正确;t=时刻,平衡位置在坐标原点的质点经过平衡位置向下振动,对应的振动图象与图b吻合,D正确。
答案 CDE
(1)振动与波两种图象综合问题的处理思路
①定位:依据已知条件明确波的图象对应的时刻,依据质点振动图象找出该时刻质点振动的位移及振动方向。再根据此位移及振动方向,在波的图象中找出该质点,则所有问题将解决。
②定时:依据已知条件找到波的图象中对应的质点,读出该质点的位移并判断其振动方向,依据位移在振动图象中确定该质点处在此位移对应的时刻。
(2)巧解波动图象与振动图象综合问题的基本方法
求解波动图象与振动图象综合类问题可采用“一分、一看、二找”的方法:
备课记录:
4-1 (2019·全国卷Ⅱ) 如图,长为l的细绳下方悬挂一小球a,绳的另一端固定在天花板上O点处,在O点正下方l的O′处有一固定细铁钉。将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时。当小球a摆至最低位置时,细绳会受到铁钉的阻挡。设小球相对于其平衡位置的水平位移为x,向右为正。下列图象中,能描述小球在开始一个周期内的xt关系的是( )
答案 A
解析 摆长为l时单摆的周期T1=2π,振幅A1=lα(α为摆角),摆长为l时单摆的周期T2=2π =π=,振幅A2=lβ(β为摆角)。根据机械能守恒定律得mgl(1-cosα)=mg(1-cosβ),利用cosα=1-2sin2,cosβ=1-2sin2,以及sin≈tan≈,sin≈tan≈,解得β=2α,故A2=A1,故A正确。
4-2 (2019·天津高考)(多选)一列简谐横波沿x轴传播,已知x轴上x1=1 m和x2=7 m处质点的振动图象分别如图1、图2所示,则此列波的传播速率可能是( )
A.7 m/s B.2 m/s
C.1.2 m/s D.1 m/s
答案 BC
解析 由振动图象可知周期T=4 s,零时刻x1
处质点在平衡位置且向下振动,而x2处质点在正的最大位移处。①若波沿x轴正方向传播,其波形如图甲所示,x2处质点的平衡位置可能在A1或A2或A3……
则有:x2-x1=λ(n=0、1、2…),
得波速v=== m/s(n=0、1、2…),
当n=0时,v=6 m/s,当n=1时,v=1.2 m/s,当n=2时,v= m/s,C正确。
②若波沿x轴负方向传播,其波形如图乙所示,x2处质点的平衡位置可能在A1或A2或A3……
则有x2-x1=λ(n=0、1、2…),
得波速v=== m/s(n=0、1、2…),
当n=0时,v=2 m/s,当n=1时,v≈0.86 m/s,B正确。
高考考向4 光的折射与全反射
例5 (2019·全国卷Ⅲ)如图,直角三角形ABC为一棱镜的横截面,∠A=90°,∠B=30°。一束光线平行于底边BC射到AB边上并进入棱镜,然后垂直于AC边射出。
(1)求棱镜的折射率;
(2)保持AB边上的入射点不变,逐渐减小入射角,直到BC边上恰好有光线射出。求此时AB边上入射角的正弦。
解析 (1)光路图及相关量如图所示。
光束在AB边上折射,由折射定律得
=n①
式中n是棱镜的折射率。由几何关系可知
α+β=60°②
由几何关系和反射定律得
β=β′=∠B③
联立①②③式,并代入i=60°得
n=④
(2)设改变后的入射角为i′,折射角为α′,由折射定律得
=n⑤
依题意,光束在BC边上的入射角为全反射的临界角θc,且sinθc=⑥
由几何关系得θc=α′+30°⑦
由④⑤⑥⑦式得此时AB边上入射角的正弦为
sini′=。
答案 (1) (2)
光的折射和全反射题型的分析思路
(1)确定要研究的光线,有时需根据题意,分析、寻找临界光线为研究对象。
(2)找入射点,确认界面,并画出法线。
(3)明确两介质折射率的大小关系。
①若光疏→光密:定有反射、折射光线。
②若光密→光疏:如果入射角大于或等于临界角,一定发生全反射。
(4)根据反射定律、折射定律列出关系式,结合几何关系,联立求解。充分考虑三角形、圆的特点,运用几何图形中的边角关系、三角函数、相似形、全等形等,仔细分析光传播过程中的几何关系。
备课记录:
5-1 (2019·江苏高考)如图所示,某L形透明材料的折射率n=2。现沿AB方向切去一角,AB与水平方向的夹角为θ。为使水平方向的光线射到AB面时不会射入空气,求θ的最大值。
答案 60°
解析 光线射到AB面时不射入空气中,则在AB面发生全反射。当恰好发生全反射时,入射角为临界角C,此时θ最大,sinC=,由几何关系得C+θm=90°,解得θm=60°。
5-2 (2019·全国卷Ⅰ)如图,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3 m。距水面4 m的湖底P
点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin53°=0.8)。已知水的折射率为。
(1)求桅杆到P点的水平距离;
(2)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍照射在桅杆顶端,求船行驶的距离。
答案 (1)7 m (2)5.5 m
解析 (1)设光束从水面射出的点到桅杆的水平距离为x1,到P点的水平距离为x2;桅杆高度为h1,P点处水深为h2;激光束在水中与竖直方向的夹角为θ。由几何关系有
=tan53°①
=tanθ②
由折射定律有
sin53°=nsinθ③
设桅杆到P点的水平距离为x,则
x=x1+x2④
联立①②③④式并代入题给数据得
x=7 m⑤
(2)设激光束在水中与竖直方向的夹角为45°时,从水面出射的方向与竖直方向夹角为i′,由折射定律有
sini′=nsin45°⑥
设船向左行驶的距离为x′,此时光束从水面射出的点到桅杆的水平距离为x1′,到P点的水平距离为x2′,则
x1′+x2′=x′+x⑦
=tani′⑧
=tan45°⑨
联立⑤⑥⑦⑧⑨式并代入题给数据得
x′=(6-3) m≈5.5 m。
阅卷现场 液面移动分析出错
例6 (2018·全国卷Ⅲ) (10分)在两端封闭、粗细均匀的U形细玻璃管内有一段水银柱,水银柱的两端各封闭有一段空气。当U形管两端竖直朝上时,左、右两边空气柱的长度分别为l1=18.0 cm和l2=12.0 cm,左边气体的压强为12.0 cmHg。现将U形管缓慢平放在水平桌面上,没有气体从管的一边通过水银逸入另一边。求U形管平放时两边空气柱的长度。在整个过程中,气体温度不变。
正解 设U形管两端竖直朝上时,左、右两边气体的压强分别为p1和p2。U形管水平放置时,两边气体压强相等,设为p,原左、右两边气体长度分别变为l1′和l2′。由力的平衡条件有
p1=p2+ρg(l1-l2)①(2分)
式中ρ为水银密度,g为重力加速度大小。
由玻意耳定律有
p1l1=pl1′②(2分)
p2l2=pl2′③(2分)
l1′-l1=l2-l2′④(2分)
由①②③④式和题给条件得
l1′=22.5 cm;l2′=7.5 cm。(2分)
答案 22.5 cm 7.5 cm
错解 设U形管两端竖直朝上时,左、右两边气体的压强分别为p1和p2。U形管水平放置时,两边气体压强相等,设为p,原左、右两边气体长度分别变为l1′和l2′。由力的平衡条件有
p1=p2+ρg(l1-l2)①(2分)
式中ρ为水银密度,g为重力加速度大小。
由玻意耳定律有
p1l1=pl1′②(2分)
p2l2=pl2′③(2分)
l1′-l1=l2′-l2④(扣2分)
由①②③④式和题给条件得l1′=9 cm,l2′=3 cm。(扣2分)
答案 9 cm 3 cm
涉及玻璃管内液柱移动的问题,需要特别注意:(1)两边玻璃管的横截面积是否相同;(2)两边液面同时移动。两边液面上升或下降的距离根据液体总体积不变求得,一边液面上升的体积等于另一边液面下降的体积(两边横截面积相同时,上升高度与下降高度相同),分析液面高度差的变化时,一定要同时关注两个液面,切不可只考虑一个液面的变化而忽略另一液面的变化。本题的错误,是仅考虑到两液面高度的变化量大小相同,而没有考虑到两液面一边是升高的另一边是下降的,没有紧扣液体体积不变这个关键点。
专题作业
1.(2019·四川宜宾二诊)(多选)图甲为一列简谐横波在t=0 s时刻的波形图,P是平衡位置为x=1 m处的质点,Q是平衡位置为x=4 m处的质点,图乙为质点Q的振动图象,则下列说法正确的是( )
A.该波的周期是0.10 s
B.该波的传播速度是40 m/s
C.该波沿x轴的正方向传播
D.t=0.10 s时,质点Q的速度方向向下
E.从t=0 s到t=0.15 s,质点P通过的路程为30 cm
答案 BCD
解析 由图甲得到该波的波长为λ=8 m,由图乙得到该波的周期为T=0.20 s,故波速为:v==40 m/s,A错误,B正确;t=0时Q向上振动,故波沿x轴正方向传播,C正确;t=0.10 s时Q点处在平衡位置上,且向下振动,D正确;从t=0 s到t=0.15 s,经历时间Δt=0.15 s=T,由于t=0 s时刻质点P
不在平衡位置和最大位移处,所以通过的路程不是3A=30 cm,E错误。
2. (2019·山东聊城一模)(多选)两列机械波在同一介质中沿相同方向传播,某时刻的波形如图所示,此时a波上某质点P的运动方向沿y轴负方向,则下列说法正确的是( )
A.两列波具有相同的波速
B.此时b波上的质点Q沿y轴正方向运动
C.一个周期内,Q质点沿x轴前进的距离是P质点的1.5倍
D.在P质点完成30次全振动的时间内Q质点可完成20次全振动
E.a波和b波在空间相遇处会产生稳定的干涉图样
答案 ABD
解析 机械波在同一介质中的传播速度相同,故A正确;由P点向下振动可判断a波的传播方向沿x轴负方向,a、b两波的传播方向一致,因此b波向x轴负方向传播,Q点向上振动,故B正确;机械波在传播时质点上下振动,不随波运动,C错误;由图象可知=,T=,又波速相同,联立可得=,Q全振动的次数nb=×30=20,因此D正确;a、b波的周期不同,频率就不同,因此不会发生稳定干涉,E错误。
3.(2019·全国卷Ⅲ)(多选)水槽中,与水面接触的两根相同细杆固定在同一个振动片上。振动片做简谐振动时,两根细杆周期性触动水面形成两个波源。两波源发出的波在水面上相遇,在重叠区域发生干涉并形成了干涉图样。关于两列波重叠区域内水面上振动的质点,下列说法正确的是( )
A.不同质点的振幅都相同
B.不同质点振动的频率都相同
C.不同质点振动的相位都相同
D.不同质点振动的周期都与振动片的周期相同
E.同一质点处,两列波的相位差不随时间变化
答案 BDE
解析 两列波相遇叠加产生干涉,一些质点的振动加强,一些质点的振动减弱,即振幅不同,A错误;各质点的振动频率、周期都与振动片相同,B、D正确;不同质点振动的相位不同(不是同时到达正的最大位移处),C错误;两列波频率相同,在同一质点处的相位差恒定,E正确。
4.(2019·辽宁卓越名校联盟二模)(多选)用双缝干涉测光的波长的实验装置如图所示,其中光源为白炽灯泡,调整实验装置使光屏上能观察到清晰的干涉条纹。关于该实验,下列说法正确的是( )
A.取下滤光片,光屏上将出现彩色的干涉条纹
B.若单缝向右平移一小段距离,光屏上相邻两条亮纹中心的距离增大
C.若将双缝间的距离d增大,光屏上相邻两条暗纹中心的距离减小
D.若将滤光片由红色换成绿色,光屏上相邻两条暗纹中心的距离减小
E.测出n条亮条纹间的距离a,则相邻两条亮条纹的间距为Δx=
答案 ACD
解析 取下滤光片,不同色光的干涉图样叠加,在光屏上将出现彩色的干涉条纹,故A正确;若单缝向右平移一小段距离,由于双缝到光屏的距离不变,则光屏上相邻两条亮纹中心的距离不变,故B错误;根据Δx=λ知,将双缝的距离d增大,则光屏上相邻两条暗纹中心的距离减小,故C正确;若将滤光片由红色换成绿色,色光的波长减小,根据Δx=λ知,光屏上相邻两条暗纹中心的距离减小,故D正确;测出n条亮条纹间的距离a,则相邻两条亮条纹的间距为Δx=,故E错误。
5. (2019·山东青岛二模)(多选)如图,光源S从水下向空气中射出一束由红光、黄光和蓝光组成的复色光,在水面上的P点分裂成a、b、c三束单色光,下列说法正确的是( )
A.c光为红色光
B.在水中传播时a光速度最大,c光波长最小
C.逐渐增大入射角,c光最先发生全反射
D.b光比a光更容易发生明显的衍射现象
E.a、b、c三种色光分别用同一双缝干涉实验装置发生干涉,a光相邻亮条纹间距最大
答案 BCE
解析 由图中a、b、c光线的偏折角大小可知navb>vc,而光在水中的波长λ=,结合faλb>λc,B正确;由sinC=及naλ0b>λ0c,所以a光比b光更容易发生明显的衍射现象,故D错误;由公式Δx=λ可知,波长越长的,间距越大,所以a光相邻亮条纹间距最大,故E正确。
6. (2020·广东省肇庆市高中毕业班统考)(多选)如图所示,在一定质量的理想气体的压强随体积变化的pV图象中,气体先后经历了ab、bc、cd、da四个过程,其中ab垂直于cd,ab垂直于V轴且与p轴平行,bc、da是两条等温线。下列判断正确的是( )
A.气体在状态a时的温度低于在状态c时的温度
B.从a→b的过程,气体分子密集程度不变,分子平均动能增加
C.从a→b→c的过程,气体密度不断减小,温度先升高后不变
D.从c→d的过程,气体放出的热量大于外界对气体做的功
E.从a→b→c→d的过程,设气体对外做功为W1,外界对气体做功为W2,气体吸热为Q1,放热为Q2,则W1-W2
查看更多