【物理】2020届一轮复习人教版第十四章第1讲机械振动作业

【物理】2020届一轮复习人教版第十四章第1讲机械振动作业

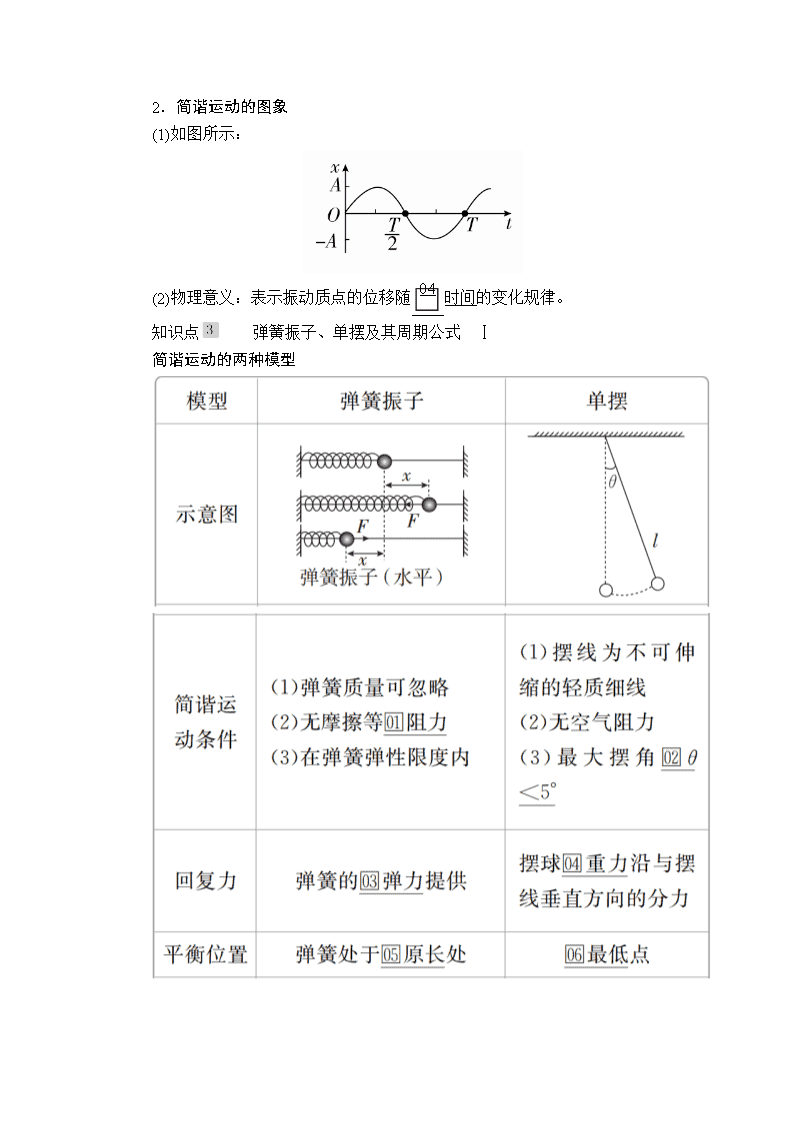
第1讲　机械振动 主干梳理 对点激活 知识点　　简谐运动　Ⅰ ‎1．简谐运动的概念 质点的位移与时间的关系遵从正弦函数的规律，即它的振动图象(x－t图象)是一条正弦曲线。‎ ‎2．平衡位置 物体在振动过程中回复力为零的位置。‎ ‎3．回复力 ‎(1)定义：使物体返回到平衡位置的力。‎ ‎(2)方向：总是指向平衡位置。‎ ‎(3)来源：属于效果力，可以是某一个力，也可以是几个力的合力或某个力的分力。‎ ‎4．描述简谐运动的物理量 知识点　　简谐运动的公式和图象　Ⅱ ‎1．表达式 ‎(1)动力学表达式：F＝－kx，其中“－”表示回复力与位移的方向相反。‎ ‎(2)运动学表达式：x＝Asin(ωt＋φ0)，其中A代表振幅，ω＝＝2πf表示简谐运动的快慢，ωt＋φ0代表简谐运动的相位，φ0叫做初相。‎ ‎2．简谐运动的图象 ‎(1)如图所示：‎ ‎(2)物理意义：表示振动质点的位移随时间的变化规律。‎ 知识点　　弹簧振子、单摆及其周期公式　Ⅰ 简谐运动的两种模型 知识点　　受迫振动和共振　Ⅰ ‎1．受迫振动 系统在驱动力作用下的振动叫做受迫振动。做受迫振动物体的周期(或频率)等于驱动力的周期(或频率)，而与物体的固有周期(或频率)无关。‎ ‎2．共振曲线 如图所示的共振曲线，表示某振动系统受迫振动的振幅A(纵坐标)随驱动力频率f(横坐标)变化的关系。驱动力的频率f跟振动系统的固有频率f0相差越小，振幅越大；驱动力的频率f等于振动系统的固有频率f0时，振幅最大。‎ 知识点　　实验：用单摆测定重力加速度 ‎1．实验原理 由单摆的周期公式T＝2π ，可得出g＝l，测出单摆的摆长l和振动周期T，就可求出当地的重力加速度g。‎ ‎2．实验器材 带中心孔的小钢球、约1 m长的细线、带有铁夹的铁架台、游标卡尺、毫米刻度尺、停表。‎ ‎3．实验步骤 ‎(1)做单摆 取约1 m长的细线穿过带中心孔的小钢球，并打一个比小孔大一些的结，然后把线的另一端用铁夹固定在铁架台上，让摆球自然下垂，在单摆平衡位置处做上标记，如图甲所示。‎ ‎(2)测摆长 用毫米刻度尺量出摆线长L(精确到毫米)，用游标卡尺测出小球直径D，则单摆的摆长l＝L＋。‎ ‎(3)测周期 将单摆从平衡位置拉开一个角度(不超过5°)，然后释放小球，记下单摆摆动30次或50次全振动的总时间，算出平均每摆动一次全振动的时间，即为单摆的振动周期T。‎ ‎(4)改变摆长，重做几次实验。‎ ‎(5)数据处理 ‎①公式法：g＝。‎ ‎②图象法：画l－T2图象，如图乙所示。‎ g＝4π2k，k＝＝。‎ ‎4．注意事项 ‎(1)悬线顶端不能晃动，需用夹子夹住，保证悬点固定。‎ ‎(2)单摆必须在同一平面内振动，且摆角小于5°。‎ ‎(3)选择在摆球摆到平衡位置处时开始计时，并数准全振动的次数。‎ ‎(4)小球自然下垂时，用毫米刻度尺量出悬线长L，用游标卡尺测量小球的直径，然后算出摆球的半径r，则摆长l＝L＋r。‎ ‎(5)选用1 m左右难以伸缩的细线。‎ 一 思维辨析 ‎1．简谐运动是匀变速运动。(　　)‎ ‎2．振幅等于振子运动轨迹的长度。(　　)‎ ‎3．简谐运动的回复力肯定不是恒力。(　　)‎ ‎4．弹簧振子每次经过平衡位置时，位移为零、动能为零。(　　)‎ ‎5．单摆无论摆角多大都是简谐运动。(　　)‎ ‎6．物体做受迫振动时，其振动频率与固有频率无关。(　　)‎ ‎7．简谐运动的图象描述的是振动质点的轨迹。(　　)‎ 答案　1.×　2.×　3.√　4.×　5.×　6.√　7.×‎ 二 对点激活 ‎1．一个弹簧振子沿x轴做简谐运动，取平衡位置O为x轴坐标原点。从某时刻开始计时，经过四分之一周期，振子具有沿x轴正方向的最大加速度。能正确反映振子位移x与时间t关系的图象是(　　)‎ 答案　A 解析　‎ 振子的最大加速度与振子的回复力成正比，方向与位移方向相反，具有正向的最大加速度，就应该具有最大的反方向的位移，振子从平衡位置开始计，并向负方向移动时，经四分之一周期振子具有沿x轴正方向的最大加速度，只有A正确，B、C、D都不符合题意。‎ ‎2．(人教版选修3－4·P17·T3改编)(多选)如图是两个单摆的振动图象，以下说法正确的是(　　)‎ A．甲、乙两个摆的振幅之比为2∶1‎ B．甲、乙两个摆的频率之比为1∶2‎ C．甲、乙两个摆的摆长之比为1∶2‎ D．以向右的方向作为摆球偏离平衡位置的位移的正方向，从t＝0起，乙第一次到达右方最大位移时，甲振动到了平衡位置，且向左运动 答案　AD 解析　由振动图象知A甲＝2 cm，A乙＝1 cm，所以甲、乙两个摆的振幅之比为2∶1，故A正确；T甲＝4 s，T乙＝8 s，所以＝＝，故B错误；由T＝2π得，＝＝，故C错误；由图象知乙第一次到达右方最大位移时为t＝2 s时，此时x甲＝0，且向左运动，故D正确。‎ ‎3．(人教版选修3－4·P21·T4改编)一个单摆在地面上做受迫振动，其共振曲线(振幅A与驱动力频率f的关系)如图所示，则(　　)‎ A．此单摆的固有周期约为0.5 s B．此单摆的摆长约为1 m C．若摆长增大，单摆的固有频率增大 D．若摆长增大，共振曲线的峰将向右移动 答案　B 解析　由共振曲线知此单摆的固有频率为0.5 Hz，固有周期为2 s，A错误；由T＝2π ，得此单摆的摆长约为1 m，B 正确；若摆长增大，单摆的固有周期增大，固有频率减小，则共振曲线的峰将向左移动，C、D错误。‎ ‎4．(人教版选修3－4·P5·T3)如下图所示，在t＝0到t＝4 s的范围内回答以下问题。‎ ‎(1)质点相对平衡位置的位移的方向在哪些时间内跟它的瞬时速度的方向相同？在哪些时间内跟瞬时速度的方向相反？‎ ‎(2)质点在第2 s末的位移是多少？‎ ‎(3)质点在前2 s内走过的路程是多少？‎ 答案　(1)在0～1 s,2～3 s内位移方向跟它的瞬时速度方向相同　在1～2 ‎ s,3～4 s内位移方向跟它的瞬时速度方向相反 (2)0 (3)20 cm 解析　(1)位移—时间图线的某点的切线的斜率即是某时刻的速度，可知，质点相对平衡位置的位移的方向在0～1 s和2～3 s内跟它的瞬时速度的方向相同，在1～2 s和3～4 s内跟瞬时速度的方向相反。‎ ‎(2)质点在第2 s末的位移是0。‎ ‎(3)质点在前2 s内走过的路程是s＝2×10 cm＝20 cm。‎ 考点细研 悟法培优 考点1　简谐运动的特征 ‎1．动力学特征 F＝－kx，“－”表示回复力的方向与位移方向相反，k是比例系数，不一定是弹簧的劲度系数。‎ ‎2．运动学特征 做简谐运动的物体加速度与物体偏离平衡位置的位移大小成正比而方向相反，为变加速运动，远离平衡位置时，x、F、a、Ep均增大，v、Ek均减小，靠近平衡位置时则相反。‎ ‎3．运动的周期性特征 相隔nT(n为正整数)的两个时刻，物体处于同一位置且振动状态相同。‎ ‎4．对称性特征 ‎(1)时间对称性：相隔或(n为正整数)的两个时刻，物体位置关于平衡位置对称，位移、速度、加速度大小相等、方向相反。如图甲所示：‎ O为平衡位置，A、B为振子偏离平衡位置最大位移处，振子t时刻在C点，t＋时刻运动到D点，则位移xD＝－xC，速度vD＝－vC，aD＝－aC。‎ ‎(2)空间对称性：如图乙所示，振子经过关于平衡位置O对称的两点P、P′(OP＝OP′)时，速度的大小、动能、势能相等，相对于平衡位置的位移大小相等。‎ 此外，振子由P到O所用时间等于由O到P′所用时间，即tPO＝tOP′。振子往复过程中通过同一段路程(如OP段)所用时间相等，即tOP＝tPO。‎ ‎5．能量特征 振动的能量包括动能Ek和势能Ep，简谐运动过程中，系统动能与势能相互转化，系统的机械能守恒。‎ 例1　(2018·辽宁鞍山模拟)(多选)弹簧振子做简谐运动，O为平衡位置，当它经过点O时开始计时，经过0.3 s，第一次到达点M，再经过0.2 s第二次到达点M，则弹簧振子的周期不可能为(　　)‎ A．0.53 s B．1.4 s C．1.6 s D．2 s E．3 s 解题探究　(1)从O点出发第一次到达M点时用时0.3 s有几种情形？‎ 提示：两种。‎ ‎(2)简谐运动中振子往复运动过程中通过同一段路程，用时相等吗？‎ 提示：相等。‎ 尝试解答　选BDE。‎ 如图甲所示，设O为平衡位置，OB(OC)代表振幅，振子从O→C所需时间为。因为简谐运动具有对称性，所以振子从M→C所用时间和从C→M所用时间相等，故＝0.3 s＋ s＝0.4 s，解得T＝1.6 s；如图乙所示，若振子一开始从平衡位置向点B运动，设点M′与点M关于点O对称，则振子从点M′经过点B到点M′所用的时间与振子从点M经过点C到点M所需时间相等，即0.2 s。振子从点O到点M′、从点M′到点O及从点O到点M所需时间相等，为＝ s，故周期为T＝0.5 s＋ s≈0.53 s，所以周期不可能为选项B、D、E。‎ 总结升华 分析简谐运动的技巧 ‎(1)分析简谐运动中各物理量的变化情况时，要以位移为桥梁，位移增大时，振动质点的回复力、加速度、势能均增大，速度、动能均减小；反之，则产生相反的变化。另外，各矢量均在其值为零时改变方向。‎ ‎(2)分析过程中要特别注意简谐运动的周期性和对称性。‎ ‎(3)如例1，若没有给出开始时刻质点的振动方向，还须分情况讨论，以防丢解。‎ ‎[变式1－1]　(多选)关于水平放置的弹簧振子所做的简谐运动，下列说法正确的是(　　)‎ A．位移的方向是由振子所在处指向平衡位置 B．加速度的方向总是由振子所在处指向平衡位置 C．经过半个周期振子经过的路程一定是振幅的2倍 D．若两时刻相差半个周期，弹簧在这两个时刻的形变量一定相等 E．经过半个周期，弹簧振子完成一次全振动 答案　BCD 解析　位移的方向始终是由平衡位置指向振子所在处，A错误；加速度的方向始终是由振子所在处指向平衡位置，B正确；经过半个周期，振子经过的路程是振幅的2倍，若两时刻相差半个周期，两时刻弹簧的形变量一定相等，C、D正确；经过一个周期，弹簧振子完成一次全振动，E错误。‎ ‎[变式1－2]　如图所示，一轻弹簧一端固定，另一端连接一物块构成弹簧振子，该物块是由a、b两个小物块粘在一起组成的。物块在光滑水平面上左右振动，振幅为A0，周期为T0。当物块向右通过平衡位置时，a、b之间的粘胶脱开；以后小物块a振动的振幅和周期分别为A和T，则A________A0，T________T0。(填“>”“<”或“＝”)‎ 答案　<　<‎ 解析　当物块向右通过平衡位置时，脱离前振子的动能Ek1＝(ma＋mb)v，脱离后振子的动能Ek2＝mav，由机械能守恒可知，平衡位置处的动能等于最大位移处的弹性势能，因此脱离后振子振幅变小；由于弹簧振子的质量减小，根据a＝－可知，在同一个位置物块a的加速度变大，即速度变化更快，故脱离后周期变小。‎ 考点2　简谐运动的图象 ‎1．图象特征 ‎(1)简谐运动的图象是一条正弦或余弦曲线，是正弦曲线还是余弦曲线取决于质点初始时刻的位置。‎ ‎(2)图象反映的是位移随时间的变化规律，随时间的增加而延伸，图象不代表质点运动的轨迹。‎ ‎(3)任一时刻在图线上对应点的切线的斜率，大小表示该时刻振子的速度大小，正负表示速度的方向，为正时，表示振子的速度沿x轴正方向；为负时，表示振子的速度沿x轴负方向。‎ ‎2．图象信息 ‎(1)由图象可以看出质点振动的振幅、周期。‎ ‎(2)可以确定某时刻质点离开平衡位置的位移。‎ ‎(3)可以确定某时刻质点的回复力、加速度和速度的方向。‎ ‎①回复力和加速度的方向：因回复力总是指向平衡位置，故回复力和加速度的方向在图象上总是指向t轴。‎ ‎②速度的方向：某时刻速度的方向既可以通过该时刻在图象上对应点的切线的斜率来判断，还可以通过下一时刻位移的变化来判断，若下一时刻位移增加，速度方向就是远离t轴；若下一时刻位移减小，速度方向就是指向t轴。‎ ‎(4)可以确定某段时间质点的位移、回复力、加速度、速度、动能、势能等的变化情况。‎ 例2　(2019·雅礼中学月考)(多选)如图甲所示为以O点为平衡位置，在A、B两点间做简谐运动的弹簧振子，图乙为这个弹簧振子的振动图象，由图可知下列说法中正确的是(　　)‎ A．在t＝0.2 s时，弹簧振子的加速度为正向最大 B．在t＝0.1 s与t＝0.3 s两个时刻，弹簧振子在同一位置 C．从t＝0到t＝0.2 s时间内，弹簧振子做加速度增大的减速运动 D．在t＝0.6 s时，弹簧振子有最小的弹性势能 E．在t＝0.2 s与t＝0.6 s两个时刻，弹簧振子速度都为零 解题探究　(1)弹簧振子的加速度方向与位移方向相同还是相反？‎ 提示：相反。‎ ‎(2)在最大位移处，速度和弹性势能有何特点？‎ 提示：速度为零，弹性势能最大。‎ 尝试解答　选BCE。‎ t＝0.2 s时，弹簧振子的位移为正向最大值，而弹簧振子的加速度与位移大小成正比，方向与位移方向相反，A错误；在t＝0.1 s与t＝0.3 s两个时刻，弹簧振子的位移相同，B正确；从t＝0到t＝0.2 s时间内，弹簧振子从平衡位置向最大位移处运动，位移逐渐增大，加速度逐渐增大，加速度方向与速度方向相反，弹簧振子做加速度增大的减速运动，C正确；在t＝0.6‎ ‎ s时，弹簧振子的位移为负向最大值，即弹簧的形变量最大，弹簧振子的弹性势能最大，D错误；t＝0.2 s与t＝0.6 s，弹簧振子都在最大位移处，速度都为零，E正确。‎ 总结升华 对振动图象的理解 ‎(1)可确定振动质点在任一时刻的位移。如图所示，t1、t2时刻质点偏离平衡位置的位移分别为x1＝7 cm，x2＝－5 cm。‎ ‎(2)可确定质点振动的振幅，图象中最大位移的绝对值就是质点振动的振幅。如图所示，质点振动的振幅是10 cm。‎ ‎(3)可确定质点振动的周期和频率，振动图象上一个完整的正弦(或余弦)图形在时间轴上拉开的“长度”表示周期，频率的大小等于周期的倒数。如图所示，OD、AE、BF的间隔都等于质点振动的周期，T＝0.2 s，频率f＝＝5 Hz。‎ ‎ (4)可确定质点的振动方向。如图所示，在t1时刻，质点正远离平衡位置向正方向运动；在t3时刻，质点正朝向平衡位置运动。‎ ‎(5)可比较各时刻质点加速度的大小和方向。例如在图中t1时刻，质点偏离平衡位置的位移x1为正，则加速度a1为负；在t2时刻，质点偏离平衡位置的位移x2为负，则加速度a2为正，因为|x1|>|x2|，所以|a1|>|a2|。‎ ‎ [变式2]　(多选)一个质点经过平衡位置O，在A、B间做简谐运动，如图a所示，它的振动图象如图b所示，设向右为正方向，下列说法正确的是(　　)‎ A．OB＝5 cm B．第0.2 s末质点的速度方向是A→O C．第0.4 s末质点的加速度方向是A→O D．第0.7 s末时质点位置在O点与A点之间 E．在4 s内完成5次全振动 答案　ACE 解析　由图b可知振幅为5 cm，则OB＝OA＝5 cm，A项正确；由图可知0～0.2 s内质点从B向O运动，第0.2 s末质点的速度方向是O→A，B项错误；由图可知第0.4 s末质点运动到A点处，则此时质点的加速度方向是A→O，C项正确；由图可知第0.7 s末时质点位置在O点与B点之间，D项错误；由图b可知周期T＝0.8 s，则在4 s内完成全振动的次数为＝5，E项正确。‎ 考点3　受迫振动与共振 自由振动、受迫振动和共振的比较 例3　(2018·唐山期末) 如图所示，一竖直圆盘转动时，固定在圆盘上的小圆柱带动一T形支架在竖直方向振动，T形支架的下面系着一弹簧和小球组成的振动系统，小球浸没在水中。当圆盘转动一会儿静止后，小球做________(填“阻尼”“自由”或“受迫”)振动。若弹簧和小球构成的系统振动频率约为3 Hz，‎ 现使圆盘以4 s的周期匀速转动，经过一段时间后，小球振动达到稳定，小球的振动频率为________ Hz。逐渐改变圆盘的转动周期，当小球振动的振幅达到最大时，此时圆盘的周期为________ s。‎ 解题探究　(1)在阻力作用下，振幅逐渐变小的振动称为________振动。‎ 提示：阻尼 ‎(2)当小球振动的振幅达到最大时，圆盘的周期________系统的固有周期。‎ 提示：等于 尝试解答　阻尼　0.25　。‎ 由于水对小球有阻力的作用，因此圆盘停止转动后，小球做阻尼振动；圆盘转动时带动小球做受迫振动，因此小球振动稳定时的振动频率等于驱动力的频率，即小球的振动频率为 Hz＝0.25 Hz；当驱动力的频率等于小球的固有频率时小球的振幅最大，即圆盘的转动频率应为3 Hz，则圆盘的周期应为 s。‎ 总结升华 对共振的理解 ‎(1)共振曲线：如图所示，横坐标为驱动力频率f，纵坐标为振幅A。它直观地反映了驱动力频率对某固有频率为f0的振动系统受迫振动振幅的影响，由图可知，f与f0越接近，振幅A越大；当f＝f0时，振幅A最大。‎ ‎(2)受迫振动中系统能量的转化：做受迫振动的系统的机械能不守恒，系统与外界时刻进行能量交换。‎ ‎[变式3－1]　关于固有频率，以下说法正确的是(　　)‎ A．固有频率是由物体本身决定的 B．物体不振动时固有频率为零 C．振幅越大，固有频率越小 D．所有物体固有频率都相同 答案　A 解析　物体做自由振动时，振动的频率与初始条件无关，仅与系统的固有特性有关(如质量、材质等)，称为固有频率，故A正确，B、C、D错误。‎ ‎[变式3－2]　(多选)某简谐振子，自由振动时的振动图象如图甲中实线所示，而在某驱动力作用下做受迫振动时，稳定后的振动图象如图甲中虚线所示，那么，此受迫振动对应的状态可能是图乙中的(　　)‎ A．a点 B．b点 C．c点 D．一定不是c点 答案　AD 解析　简谐振子自由振动时，设周期为T1；而在某驱动力作用下做受迫振动时，设周期为T2；显然T1f2；题图乙中c点处代表发生共 振，驱动力频率等于固有频率f1；做受迫振动时，驱动力频率f2

查看更多