2020届二轮复习专题八　应用数学知识和方法处理物理问题课件（30张）

2020届二轮复习专题八　应用数学知识和方法处理物理问题课件（30张）

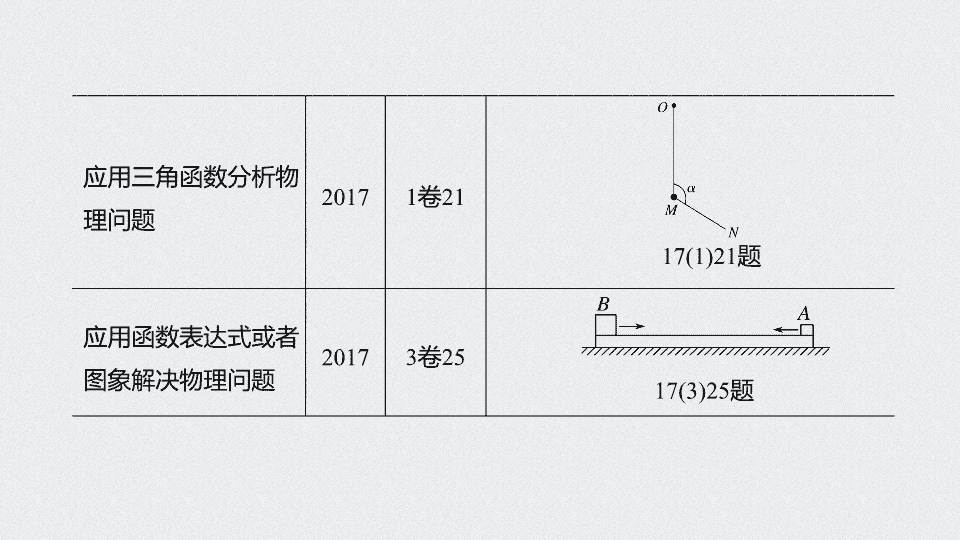
专题八 　 应用数学 知识和 方法处理物理问题 第一部分 　 专题复习 高考命题轨迹 高考命题点 命题轨迹 情境图 应用正、余弦定理、几何图形及数学推理解决物理问题 2016 3 卷 34(2)   2018 1 卷 25 、 34(1) 2 卷 25 、 34(2) 3 卷 25 、 34(2 ) 16(3)34(2) 题　 18(1)25 题 18(1)34(1 ) 题 18(2)25 题　　 18(2)34(2) 题 18(3)25 题　　 18(3)34(2) 题 应用三角函数分析物理问题 2017 1 卷 21 　　　　 应用函数表达式或者图象解决物理问题 2017 3 卷 25 17(1)21 题 17(3)25 题 数学方程式、不等式、微元法和归纳法的应用 2016 3 卷 25 、 35(2) 　　　　 2017 1 卷 25 , 2 卷 25 , 3 卷 33(2) 16(3)25 题　　 16(3)35(2) 题 17(3)33(2) 题 17(2)25 题 数学推导和结论分析 2015 1 卷 25 、 35(2) ， 2 卷 25 　　　　 2016 1 卷 16 、 25, 2 卷 25 15(1)25 题　　　　　 15(1)35(2 ) 题 15(2)25 题　　 16(1)16 题 16(1)25 题　　　 16(2)25 题 高考题型 1 应用正、余弦定理和几何图形解决物理问题 内容索引 NEIRONGSUOYIN 高考题型 2 应用 三角函数分析物理问题 高考题型 3 应用 函数表达式或者图象解决物理问题 高考题型 4 数学 方程式和归纳法的 应用 高考题型 5 数学 推导和结论分析 应用正、余弦定理和几何图形解决物理问题 题型：选择题： 5 年 2 考 高考题型 1 例 1 　 (2019· 山东日照市 3 月模拟 ) 如图 1 所示，两个质量分别 为 m 、 m 的小圆环 A 、 B 用不可伸长的细线连着，套在一个竖直固定的大圆环上，大圆环的圆心为 O . 系统平衡时，细线所对的圆心角为 90° ，大圆环和小圆环之间的摩擦力及细线的质量忽略不计，重力加速度大小用 g 表示，下列判断正确的 是 A. 小圆环 A 、 B 受到大圆环的支持力之比 是 ∶ 1 B. 小圆环 A 受到大圆环的支持力与竖直方向的夹角为 15° C. 细线与水平方向的夹角为 30° D . 细线的拉力大小 为 mg √ 图 1 解析　 对 A 和 B 进行受力分析，根据平行四边形定则作出重力和支持力的合力，此合力的大小等于绳子的拉力的大小，设 A 、 B 所受的支持力与竖直方向的夹角分别为 α 和 β ，如图所示： 由于 F T ＝ F T ′ ， α ＋ β ＝ 90° 由题图根据几何知识可以知道，细线与水平方向的夹角为 180° － (45° ＋ 30°) － 90° ＝ 15° ，故选项 C 错误 . 应用 三角函数分析物理问题 题型：选择或者计算题： 5 年 1 考 高考题型 2 例 2 　 ( 2019· 山西临汾市二轮复习模拟 ) 如图 2 所示是一旅行箱，它既可以在地面上推着行走，也可以在地面上拉着行走 . 已知该旅行箱的总质量为 15 kg ，一旅客用斜向上的拉力拉着旅行箱在水平地面上做匀速直线运动，若拉力的最小值为 90 N ，此时拉力与水平方向间的夹角为 θ ，重力加速度大小为 g ＝ 10 m/s 2 ， sin 37° ＝ 0.6 ，旅行箱受到地面的阻力与其受到地面的支持力成正比，比值为 μ ， 则 A. μ ＝ 0.5 ， θ ＝ 37° B. μ ＝ 0.5 ， θ ＝ 53° C. μ ＝ 0.75 ， θ ＝ 53° D. μ ＝ 0.75 ， θ ＝ 37 ° √ 图 2 解析　 对旅行箱受力分析，如图所示： 当 α － θ ＝ 0° 时， F 有最小值，故 F ＝ G sin α ＝ 90 N ，故 α ＝ 37° ， 故 μ ＝ tan 37° ＝ 0.75 ， θ ＝ 37° ，故选 D. 根据平衡条件，水平方向，有： F cos θ － F f ＝ 0 ， 竖直方向，有： F N ＋ F sin θ － G ＝ 0 ， 其中： F f ＝ μF N ， 应用函数表达式或者图象解决物理问题 题型：选择题： 5 年 1 考 高考题型 3 例 3 　 (2019· 湖北武汉市四月调研 ) 某质点做匀加速直线运动，经过时间 t 速度由 v 0 变为 k v 0 ( k >1) ，位移大小为 x . 则在随后的 4 t 内，该质点的位移大小为 √ 数学方程式和归纳法的应用 题型：计算题： 5 年 2 考 高考题型 4 例 4 　 (2019· 山东日照市 3 月模拟 ) 如图 3 所示，在平面直角坐标系 xOy 的第一、二象限内，存在以虚线 OM 为边界的匀强电场和匀强磁场 . 匀强电场方向沿 y 轴负方向，匀强磁场方向垂直于 xOy 平面向里，虚线 OM 与 x 轴负方向成 45° 角 . 一质量为 m 、电荷量为＋ q 的带电粒子从坐标原点 O 处以初速度 v 0 沿 x 轴正方向运动，粒子每次到达 x 轴将反弹，第一次反弹无能量损失，以后每次反弹水平分速度不变、竖直分速度大小均减为反弹前 的 ， 方向相反 . 电场强度大小 等于 ， 磁感应强度大小 等于 ， 求： ( 不计粒子重力，题中各物理量单位均为国际单位，计算结果可用分式表示 ) (1) 带电粒子第三次经过 OM 时的坐标 ； 图 3 答案　 ( － 2 d ,2 d ) 　 解析　 设 磁感应强度大小为 B ，粒子进入磁场，根据左手定则， 粒子运动轨迹如图所示，由图可知，带电粒子第三次经过 OM 时的坐标为 ( － 2 d ,2 d ) ； (2) 带电粒子第三次到达 OM 时经过的时间； 设粒子从第一次沿 y 轴负方向经过 OM 到第一次在 x 轴反弹所用时间为 t 1 ，沿 y 轴方向： v y 0 2 － v 0 2 ＝ 2 ar ， v y 0 ＝ v 0 ＋ at 1 (3) 带电粒子从第二次进入电场开始，沿电场方向运动的总路程 . 解析　 因 粒子第二次进入电场做类平抛运动，故到达 x 轴时的水平分速度为 v 0 竖直方向： v y 2 ＝ 2 a (2 d ) …… 数学推导和结论分析 题型：计算题： 5 年 2 考 高考题型 5 例 5 　 (2019· 山东德州市上学期期末 ) 如图 4 所示，宽度为 L 的光滑固定金属导轨由水平部分和倾斜部分组成，水平部分足够长，倾斜部分与水平面的夹角为 30°. 导轨水平部分处于竖直向上的匀强磁场中，倾斜部分处于斜向上与导轨平面垂直的匀强磁场中，两磁场的磁感应强度大小均为 B . 导体棒 ab 和 cd 均与导轨垂直且分别置于导轨的倾斜部分上和水平部分上并保持静止，现将导体棒 ab 在距导轨水平部分高度为 h 处释放，导体棒 ab 在到达 MN 处之前已达到稳定的运动状态，在导体棒 ab 到达 MN 时再释放导体棒 cd ，导体棒 ab 在 MN 处由倾斜部分进入水平部分时无能量损失 . 已知导体棒 ab 质量为 m ，电阻为 r ，导体棒 cd 质量也为 m ，电阻为 2 r ，导轨电阻忽略不计，两导体棒始终与导轨接触良好，当地重力加速度为 g ，求 ： (1) 导体棒 ab 到达 MN 之前稳定运动时的速度大小 ； 图 4 解析　 导体棒 ab 到达 MN 之前 稳定运动时，由平衡条件得 mg sin 30° ＝ ILB (2) 整个过程中导体棒 ab 产生的焦耳热； 解析　 导体 棒 ab 进入水平部分后， ab 和 cd 组成 的系统动量守恒 m v ＝ 2 m v ′ (3) 整个过程中通过导体棒 ab 某一横截面的电荷量 . 解析　 导体 棒 ab 自开始运动至到达 MN 的过程中，通过导体棒 ab 某一横截面的电荷量 对导体棒 cd 的运动过程运用动量定理： 本课结束