2018届二轮复习动量和能量观点的应用课件(46张)(全国通用)
第
2
讲 动量和能量观点的应用
-
2
-
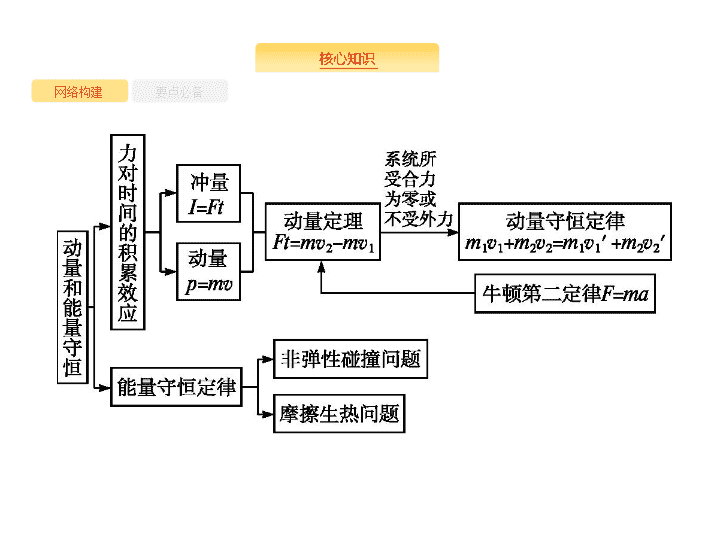
网络构建
要点必备
-
3
-
网络构建
要点必备
1
.
动量定理
(1)
内容
:
物体在一个过程始末的动量变化量等于它在这个过程中所受力的冲量。
(2)
表达式
:
F
·Δ
t=
Δ
p=p'-p
。
(3)
矢量性
:
动量变化量的方向与合力的方向相同
,
可以在某一方向上应用动量定理。
2
.
动量、动能、动量的变化量的关系
(1)
动量的变化量
:Δ
p=p'-p
。
(2)
动能和动量的关系
:
3
.
动量守恒定律
(1)
条件
:
系统不受外力或系统所受外力的矢量和为零。
(2)
表达式
:
m
1
v
1
+m
2
v
2
=
。
4
.
能量的观点
:
在涉及系统内能量的转化问题时
,
常用能量守恒定律。
m
1
v
1
'+
m
2
v
2
'
-
4
-
1
2
3
1
.
(2017
全国
Ⅰ
卷
)
将质量为
1
.
00 kg
的模型火箭点火升空
,50 g
燃烧的燃气以大小为
600 m/s
的速度从火箭喷口在很短时间内喷出。在燃气喷出后的瞬间
,
火箭的动量大小为
(
喷出过程中重力和空气阻力可忽略
)(
)
A.30 kg·m/s
B.5
.
7
×
10
2
kg·m/s
C.6
.
0
×
10
2
kg·m/s D.6
.
3
×
10
2
kg·m/s
A
解析
根据动量守恒定律得
:0
=Mv
1
-mv
2
,
故火箭的动量与燃气的动量等大反向。故
p=Mv
1
=mv
2
=
0
.
05
kg
×
600
m/s
=
30
kg
·
m/s
。
考点定位
:
动量定理
命题能力点
:
侧重考查理解能力
解题思路与方法
:
以火箭和燃气为研究对象
,
在燃气喷出的瞬间动量守恒。
-
5
-
1
2
3
2
.
(2016
全国
Ⅰ
卷
)
某游乐园入口旁有一喷泉
,
喷出的水柱将一质量为
M
的卡通玩具稳定地悬停在空中。为计算方便起见
,
假设水柱从横截面积为
S
的喷口持续以速度
v
0
竖直向上喷出
;
玩具底部为平板
(
面积略大于
S
);
水柱冲击到玩具底板后
,
在竖直方向水的速度变为零
,
在水平方向朝四周均匀散开。忽略空气阻力。已知水的密度为
ρ
,
重力加速度大小为
g
。求
:
(1)
喷泉单位时间内喷出的水的质量
;
(2)
玩具在空中悬停时
,
其底面相对于喷口的高度。
-
6
-
1
2
3
-
7
-
1
2
3
-
8
-
1
2
3
考点定位
:
动量定理
机械能守恒定律
命题能力点
:
侧重考查理解能力
解题思路与方法
:
本题考查了动量定理的应用
,
要知道玩具在空中悬停时
,
受力平衡
,
合力为零
,
也就是水对玩具的冲力等于玩具的重力。本题的难点是求水对玩具的冲力
,
而求这个冲力的关键是单位时间内水的质量
,
注意空中的水柱并非圆柱体
,
要根据流量等于初刻速度乘以时间后再乘以喷泉出口的面积
S
求出流量
,
最后根据
m=
ρ
V
求质量。
-
9
-
1
2
3
3
.
(2016
全国
Ⅲ
卷
)
如图
,
水平地面上有两个静止的小物块
a
和
b
,
其连线与墙垂直
:
a
和
b
相距
l
,
b
与墙之间也相距
l
;
a
的质量为
m
,
b
的质量
为
m
。两物块与地面间的动摩擦因数均相同。现使
a
以初速度
v
0
向右滑动。此后
a
与
b
发生弹性碰撞
,
但
b
没有与墙发生碰撞。重力加速度大小为
g
。求物块与地面间的动摩擦因数满足的条件。
-
10
-
1
2
3
-
11
-
1
2
3
-
12
-
1
2
3
考点定位
:
动量守恒定律
能量守恒定律的应用
命题能力点
:
侧重考查理解能力
方法技巧
:
本题要按时间顺序分析物体的运动过程
,
知道弹性碰撞过程遵守动量守恒和能量守恒
,
要结合功能关系分析
b
与墙不相撞的条件。
-
13
-
1
2
3
命题规律研究及预测
分析高考试题可以看出
,
高考命题突出动量定理、动量守恒定律、碰撞模型的考查。动量守恒定律与运动学公式及动量守恒定律与能量守恒定律的综合题也是考查的重点。题型一般为选择题。
在
2018
年的备考过程中要尤其注重动量守恒定律与能量守恒定律的综合题的复习。
-
14
-
考点一
考点二
考点三
动量、冲量、动量定理
(L)
典题
1
(2017
山东泰安模拟
)
如图所示
,
竖直平面内有一半圆槽
,
A
、
C
等高
,
B
为圆槽最低点
,
小球从
A
点正上方
O
点静止释放
,
从
A
点切入圆槽
,
刚好能运动至
C
点。设球在
AB
段和
BC
段运动过程中
,
运动时间分别为
t
1
、
t
2
,
合外力的冲量大小为
I
1
、
I
2
,
则
(
)
A.
t
1
>t
2
B.
t
1
=t
2
C.
I
1
>I
2
D.
I
1
=I
2
C
-
15
-
考点一
考点二
考点三
解析
小球从
A
点正上方
O
点静止释放
,
刚好能运动至
C
点
,
说明在圆弧内要克服摩擦力做功
,
因此在
AB
段平均速率大于
BC
段平均速率
,
两段路程相等
,
所以
t
1
I
2
,C
正确
,D
错误。
-
16
-
考点一
考点二
考点三
典题
2
皮球从某高度落到水平地板上
,
每弹跳一次上升的高度总等于前一次的
0
.
64,
且每次球与地板接触的时间相等。若空气阻力不计
,
与地板碰撞时
,
皮球重力可忽略。
(1)
求相邻两次球与地板碰撞的平均冲力大小之比是多少
?
(2)
若用手拍这个球
,
使其保持在
0
.
8 m
的高度上下跳动
,
则每次应给球施加的冲量为多少
?(
已知球的质量
m=
0
.
5 kg,
g
取
10 m/s
2
)
答案
(1)5
∶
4
(2)1
.
5 N·s
方向竖直
向下
-
17
-
考点一
考点二
考点三
解析
(1)
由题意可知
,
碰撞后的速度是碰撞前的
0
.
8
。设皮球所处的初始高度为
H
,
与地板第一次碰撞前瞬时速度大小为
,
第一次碰撞后瞬时速度大小
(
亦为第二次碰撞前瞬时速度大小
)
v
1
和第二次碰撞后瞬时速度大小
v
2
满足
v
2
=
0
.
8
v
1
=
0
.
8
2
v
0
。设两次碰撞中地板对球的平均冲力分别为
F
1
、
F
2
,
选竖直向上为正方向
,
根据动量定理
,
有
F
1
t=mv
1
-
(
-mv
0
)
=
1
.
8
mv
0
F
2
t=mv
2
-
(
-mv
1
)
=
1
.
8
mv
1
=
1
.
44
mv
0
则
F
1
∶
F
2
=
5
∶
4
。
(2)
欲使球跳起
0
.
8
m,
应使球由静止下落的高度为
h
=
m
=
1
.
25
m,
球由
1.25
m
落到
0.8
m
处的速度为
v=
3
m/s,
则应在
0
.
8
m
处给球的冲量为
I=mv=
1
.
5
N
·
s,
方向竖直向下。
-
18
-
考点一
考点二
考点三
规律方法应用动量定理解题时的五点注意
(1)
动量定理表明冲量既是使物体动量发生变化的原因
,
又是物体动量变化的量度。这里所说的冲量是物体所受的合外力的冲量
(
或者说是物体所受各外力冲量的矢量和
)
。
(2)
动量定理的研究对象是一个质点
(
或可视为一个物体的系统
)
。
(3)
动量定理是过程定理
,
解题时必须明确过程及初末状态的动量。
(4)
动量定理的表达式是矢量式
,
在一维情况下
,
各个矢量必须选一个规定正方向。二维情况下要注意矢量减法。
(5)
对过程较复杂的运动
,
可分段用动量定理
,
也可整个过程用动量定理。
-
19
-
考点一
考点二
考点三
动量守恒定律及应用
(H)
解题策略
策略
1:
弹性碰撞与非弹性碰撞
碰撞过程遵从动量守恒定律。如果碰撞过程中机械能守恒
,
这样的碰撞叫弹性碰撞
;
如果碰撞过程中机械能不守恒
,
这样的碰撞叫非弹性碰撞。
策略
2:
应用动量守恒定律的解题步骤
(1)
明确研究对象
(
系统包括哪几个物体及研究的过程
);
(2)
进行受力分析
,
判断系统动量是否守恒
(
或某一方向上动量是否守恒
);
(3)
规定正方向
,
确定初、末状态动量
;
(4)
由动量守恒定律列式求解
;
(5)
必要时对结果进行讨论。
-
20
-
考点一
考点二
考点三
典题
3
(
多选
)
如图所示
,
小车
AB
放在光滑水平面上
,
A
端固定一个轻弹簧
,
B
端粘有油泥
,
AB
总质量为
m'
,
质量为
m
的木块
C
放在小车上
,
用细绳连接于小车的
A
端并使弹簧压缩
,
开始时
AB
和
C
都静止
,
当突然烧断细绳时
,
C
被释放
,
使
C
离开弹簧向
B
端冲去
,
并跟
B
端油泥粘在一起
,
忽略一切摩擦
,
以下说法正确的是
(
)
A.
弹簧伸长过程中
C
向右运动
,
同时
AB
也向右运动
B.
C
与
B
碰前
,
C
与
AB
的速率之比为
m'
∶
m
C.
C
与油泥粘在一起后
,
AB
立即停止运动
D.
C
与油泥粘在一起后
,
AB
继续向右运动
BC
-
21
-
考点一
考点二
考点三
解析
小车、物块和弹簧组成的系统动量守恒
,
开始总动量为零
,
当弹簧伸长的过程中
,
C
向右运动
,
则小车向左运动
,
故
A
错误。规定向右为正方向
,
在
C
与
B
碰前
,
根据动量守恒得
,0
=mv
C
-m'v
,
解得
v
C
∶
v =
m'
∶
m
,
故
B
正确。因为小车、物块和弹簧组成的系统动量守恒
,
开始总动量为零
,
当
C
与泥粘在一起时
,
总动量仍然为零
,
则小车停止运动
,
故
C
正确
,D
错误。故选
BC
。
-
22
-
考点一
考点二
考点三
典题
4
如图所示
,
一质量
m'=
3
.
0 kg
的长方形木板
B
放在光滑水平地面上
,
在其右端放一个质量
m=
1
.
0 kg
的小木块
A
。给
A
和
B
以大小均为
4
.
0 m/s
、方向相反的初速度
,
使
A
开始向左运动
,
B
开始向右运动
,
A
始终没有滑离木板。在小木块
A
做加速运动的时间内
,
木板速度大小可能是
(
)
A.1
.
8 m/s B.2
.
4 m/s
C.2
.
8 m/s D.3
.
0 m/s
B
-
23
-
考点一
考点二
考点三
典题
5
(2017
山东威海模拟
)
质量为
m
的物块甲以
3 m/s
的速度在光滑水平面上运动
,
有一轻弹簧固定其上
,
另一质量也为
m
的物体乙以
4 m/s
的速度与甲相向运动
,
如图所示
,
则
(
)
A.
甲、乙两物块在弹簧压缩过程中
,
由于弹力作用
,
系统动量不守恒
B.
当两物块相距最近时
,
甲物块的速率为零
C.
当甲物块的速率为
1 m/s
时
,
乙物块的速率可能为
2 m/s,
也可能为
0
D.
甲物块的速率可能达到
6 m/s
C
-
24
-
考点一
考点二
考点三
解析
甲、乙两物块在弹簧压缩过程中
,
由于弹力是系统内力
,
系统合外力为零
,
所以动量守恒
,
选项
A
错误
;
当两物块相距最近时
,
它们的速度相同
,
设为
v
,
取水平向右为正方向
,
由动量守恒定律有
mv
乙
-mv
甲
=
2
mv
,
代入数据
,
可得
v=
0
.
5
m/s,
选项
B
错误
;
当甲物块的速率为
1
m/s
时
,
其方向可能向左
,
也可能向右
,
当水平向左时
,
根据动量守恒定律可得
,
乙物块的速率为
2
m/s;
当水平向右时
,
同理可得
,
乙物块的速率为
0,
所以选项
C
正确
;
因为整个过程中
,
系统的机械能不可能增加
,
选项
D
错误。
-
25
-
考点一
考点二
考点三
规律方法
1
.
对象为一个系统
,
应优先考虑应用动量守恒定律。
2
.
一般碰撞的三个制约关系
一般碰撞介于弹性碰撞和完全非弹性碰撞之间
:
动量守恒
,
机械能
(
或动能
)
有损失
,
遵循以下三个制约关系
:
(1)
动量制约
:
碰撞过程中必须受到动量守恒定律的制约
,
总动量的方向恒定不变
,
即
p
1
+p
2
=p
1
'+p
2
'
。
(2)
动能制约
:
在碰撞过程中
,
碰撞双方的总动能不会增加
,
即
E
k1
+E
k2
≥
E
k1
'+E
k2
'
。
(3)
运动制约
:
碰撞要受到运动的合理性要求的制约
,
如果碰前两物体同向运动
,
碰撞后原来在前面的物体速度必增大
,
且大于或等于原来在后面的物体的碰后速度。
-
26
-
考点一
考点二
考点三
动量与能量的综合应用
(H)
解题策略
1
.
弄清有几个物体参与运动
,
并划分清楚物体的运动过程。
2
.
进行正确的受力分析
,
明确各过程的运动特点。
3
.
光滑的平面或曲面
,
还有不计阻力的抛体运动
,
机械能一定守恒
;
碰撞过程、子弹打击木块、不受其他外力作用的两物体相互作用问题
,
一般考虑用动量守恒定律分析。
4
.
如含摩擦生热问题
,
则考虑用能量守恒定律分析。
-
27
-
考点一
考点二
考点三
典题
6
(2017
云南楚雄模拟
)
如图所示
,
在光滑的水平面上静止放一质量为
m
的木板
B
,
木板表面光滑
,
左端固定一轻质弹簧。质量为
2
m
的木块
A
以速度
v
0
从板的右端水平向左滑上木板
B
。在木块
A
与弹簧相互作用的过程中
,
下列判断正确的是
(
)
D
-
28
-
考点一
考点二
考点三
-
29
-
考点一
考点二
考点三
典题
7
(2017
湖南衡阳模拟
)
如图甲所示
,
在高
h=
0
.
8 m
的水平平台上放置一质量为
m'=
0
.
9 kg
的小木块
(
视为质点
),
距平台右边缘
d=
2 m
。一质量为
m=
0
.
1 kg
的子弹沿水平方向射入小木块并留在其中
(
作用时间极短
),
然后一起向右运动
,
在平台上运动的
v
2
-
x
关系如图乙所示
,
最后小木块从平台边缘滑出并落在距平台右侧水平距离为
s=
1
.
6 m
的地面上。
g
取
10 m/s
2
,
求
:
(1)
小木块滑出平台时的速度
;
(2)
子弹射入小木块前的速度
;
(3)
子弹射入木块前至木块滑出平台时
,
系统所产生的内能。
-
30
-
考点一
考点二
考点三
答案
(1)4 m/s
(2)80 m/s
(3)72
J
-
31
-
考点一
考点二
考点三
典题
8
两滑块
a
、
b
沿水平面上同一条直线运动
,
并发生碰撞
,
碰撞后两者粘在一起运动
,
经过一段时间后
,
从光滑路段进入粗糙路段。两者的位置
x
随时间
t
变化的图象如图所示。求
:
(1)
滑块
a
、
b
的质量之比
;
(2)
整个运动过程中
,
两滑块克服摩擦力做的功与因碰撞而损失的机械能之比。
答案
(1)1
∶
8
(2)1
∶
2
-
32
-
考点一
考点二
考点三
-
33
-
考点一
考点二
考点三
思维激活
1
.x
-
t
图象能获取
a
、
b
两滑块碰前、碰后的速度吗
?
2
.
两滑块的最终状态是什么
?
两滑块的能量是如何转化的
?
答案
1
.
能
2
.
静止
-
34
-
考点一
考点二
考点三
动量、冲量、动量定理
1
.
(2017
湖北黄冈模拟
)
一小球从水平地面上方无初速释放
,
与地面发生碰撞后反弹至速度为零
,
假设小球与地面碰撞没有机械能损失
,
运动时的空气阻力大小不变
,
下列说法正确的是
(
)
A.
上升过程中小球动量改变量等于该过程中空气阻力的冲量
B.
小球与地面碰撞过程中
,
地面对小球的冲量为零
C.
下落过程中小球动能的改变量等于该过程中重力做的功
D.
从释放到反弹至速度为零过程中小球克服空气阻力做的功等于重力做的功
D
-
35
-
考点一
考点二
考点三
解析
根据动量定理可知
,
上升过程中小球动量改变量等于该过程中重力和空气阻力的合力的冲量
,
选项
A
错误
;
小球与地面碰撞过程中
,
由动量定理得
Ft-mgt=mv
2
-
(
-mv
1
),
可知地面对小球的冲量
Ft
不为零
,
选项
B
错误
;
下落过程中小球动能的改变量等于该过程中重力和空气阻力做功代数和
,
选项
C
错误
;
由能量守恒关系可知
,
从释放到反弹至速度为零过程中小球克服空气阻力做的功等于重力做的功
,
选项
D
正确。
-
36
-
考点一
考点二
考点三
2
.
(
多选
)
一粒钢珠从静止状态开始自由下落
,
然后陷入泥潭中。若把在空中下落的过程称为过程
Ⅰ
,
进入泥潭直到停止的过程称为过程
Ⅱ
,
则
(
)
A.
过程
Ⅰ
中钢珠的动量的改变量等于重力的冲量
B.
过程
Ⅱ
中阻力的冲量的大小等于过程
Ⅰ
中重力的冲量的大小
C.
Ⅰ
、
Ⅱ
两个过程中合外力的总冲量等于零
D.
过程
Ⅱ
中钢珠的动量的改变量等于零
AC
-
37
-
考点一
考点二
考点三
解析
根据动量定理可知
,
在过程
Ⅰ
中
,
钢珠从静止状态自由下落。不计空气阻力
,
小球所受的合外力即为重力
,
因此钢珠的动量的改变量等于重力的冲量
,
选项
A
正确
;
过程
Ⅱ
中阻力的冲量的大小等于过程
Ⅰ
中重力的冲量的大小与过程
Ⅱ
中重力的冲量的大小之和
,
显然
B
选项不对
;
在
Ⅰ
、
Ⅱ
两个过程中
,
钢珠动量的改变量各不为零
,
且它们大小相等、方向相反
,
但从整体看
,
钢珠动量的改变量为零
,
故合外力的总冲量等于零
,
故
C
选项正确
,D
选项错误。因此
,
本题的正确选项为
A
、
C
。
-
38
-
考点一
考点二
考点三
动量守恒定律及应用
3
.
(
多选
)(2017
江西南昌模拟
)
A
、
B
两物体在光滑水平面上沿同一直线运动
,
图表示发生碰撞前后的
v
-
t
图线
,
由图线可以判断正确的是
(
)
A.
A
、
B
的质量比为
3
∶
2
B.
A
、
B
作用前后总动量守恒
C.
A
、
B
作用前后总动量不守恒
D.
A
、
B
作用前后总动能不变
ABD
-
39
-
考点一
考点二
考点三
解析
A
、
B
碰撞前后动量守恒
,
根据动量守恒定律
:
m
A
×
6
+m
B
×
1
=m
A
×
2
+m
B
×
7
得
:
m
A
∶
m
B
=
3
∶
2,
故
A
正确
,B
正确
,C
错误。
可见碰撞前后总动能不变
,D
正确。
故选
A
、
B
、
D
。
-
40
-
考点一
考点二
考点三
4
.
(2017
黑龙江哈尔滨模拟
)
如图所示
,
在光滑绝缘的水平直轨道上有两个带电小球
a
和
b
,
a
球质量为
2 m
、电荷量为
+q
,
b
球质量为
m
、电荷量为
+
2
q
,
两球相距较远且相向运动。某时刻
a
、
b
球的速度大小依次为
v
和
1
.
5
v
,
由于静电斥力的作用
,
它们不会相碰。则下列叙述正确的是
(
)
A.
两球相距最近时
,
速度大小相等、方向相反
B.
a
球和
b
球所受的静电斥力对两球始终做负功
C.
a
球一直沿原方向运动
,
b
球要反向运动
D.
a
、
b
两球都要反向运动
,
但
b
球先反向
C
-
41
-
考点一
考点二
考点三
解析
水平方向系统动量守恒
,
由完全非弹性碰撞的知识可知
,
当两球速度大小相等、方向相同时
,
系统损失机械能最大
,
两球相距最小
,
故
A
错误
;
由题意可知
,
a
球初动量大于
b
球初动量
,
因此系统总动量水平向右
,
故
b
球运动过程中将反向运动而
a
球将一直沿原方向运动
,
因此静电斥力对
b
球先做负功后做正功
,
故
B
、
D
错误
,C
正确。
-
42
-
考点一
考点二
考点三
动量与能量的综合应用
5
.
(2017
四川成都模拟
)
如图所示
,
小车静止在光滑水平面上
,
AB
是小车内半圆弧轨道的水平直径
,
现将一小球从距
A
点正上方
h
高处由静止释放
,
小球由
A
点沿切线方向经半圆轨道后从
B
点冲出
,
在空中能上升的最大高度为
0
.
8
h
,
不计空气阻力。下列说法正确的是
(
)
A
.
在相互作用过程中
,
小球和小车组成的系统动量守恒
B.
小球离开小车后做竖直上抛运动
C.
小球离开小车后做斜上抛运动
D.
小球第二次冲出轨道后在空中能上升的最大高度为
0
.
6
h
B
-
43
-
考点一
考点二
考点三
解析
小球与小车组成的系统在水平方向所受合外力为零
,
水平方向系统动量守恒
,
但系统整体所受合外力不为零
,
系统动量不守恒
,
故
A
错误
;
小球与小车组成的系统在水平方向动量守恒
,
小球由
A
点离开小车时系统水平方向动量为零
,
小球与小车水平方向速度为零
,
小球离开小车后做竖直上抛运动
,
故
B
正确、
C
错误
;
小球第一次车中运动过程中
,
摩擦力做负功
,
由动能定理得
mg
(
h-
0
.
8
h
)
-W
F
f
=
0,
W
F
f
为小球克服摩擦力做功大小
,
解得
W
F
f
=
0
.
2
mgh
,
即小球第一次在车中滚动损失的机械能为
0
.
2
mgh
,
由于小球第二次在车中滚动时
,
对应位置速度变小
,
因此小车给小球的弹力变小
,
摩擦力变小
,
摩擦力做功小于
0
.
2
mgh
0
,
机械能损失小于
0
.
2
mgh
0
,
因此小球再次离开小车时
,
能上升的高度大于
0
.
6
h
,
故
D
错误
;
故选
B
。
-
44
-
考点一
考点二
考点三
6
.
如图所示
,
小球
A
质量为
m
,
系在细线的一端
,
线的另一端固定在
O
点
,
O
点到光滑水平面的距离为
h
。物块
B
和
C
的质量分别是
5
m
和
3
m
,
B
与
C
用轻弹簧拴接
,
置于光滑的水平面上
,
且
B
物块位于
O
点正下方。现拉动小球使细线水平伸直
,
小球由静止释放
,
运动到最低点时与物块
B
发生正碰
(
碰撞时间极短
),
反弹后上升到最高点时到水平面的距离为
。小球与物块均视为质点
,
不计空气阻力
,
重力加速度为
g
,
求碰撞过程中
B
物块受到的冲量大小及碰后轻弹簧获得的最大弹性势能。
-
45
-
考点一
考点二
考点三
解析
设小球运动到最低点与物块
B
碰撞前的速度大小为
v
1
,
取小球运动到最低点时的重力势能为零
,
根据机械能守恒定律有
:
-
46
-
考点一
考点二
考点三