【物理】2020高考二轮复习专题练破解计算题必备的四项基本能力（解析版）

【物理】2020高考二轮复习专题练破解计算题必备的四项基本能力（解析版）

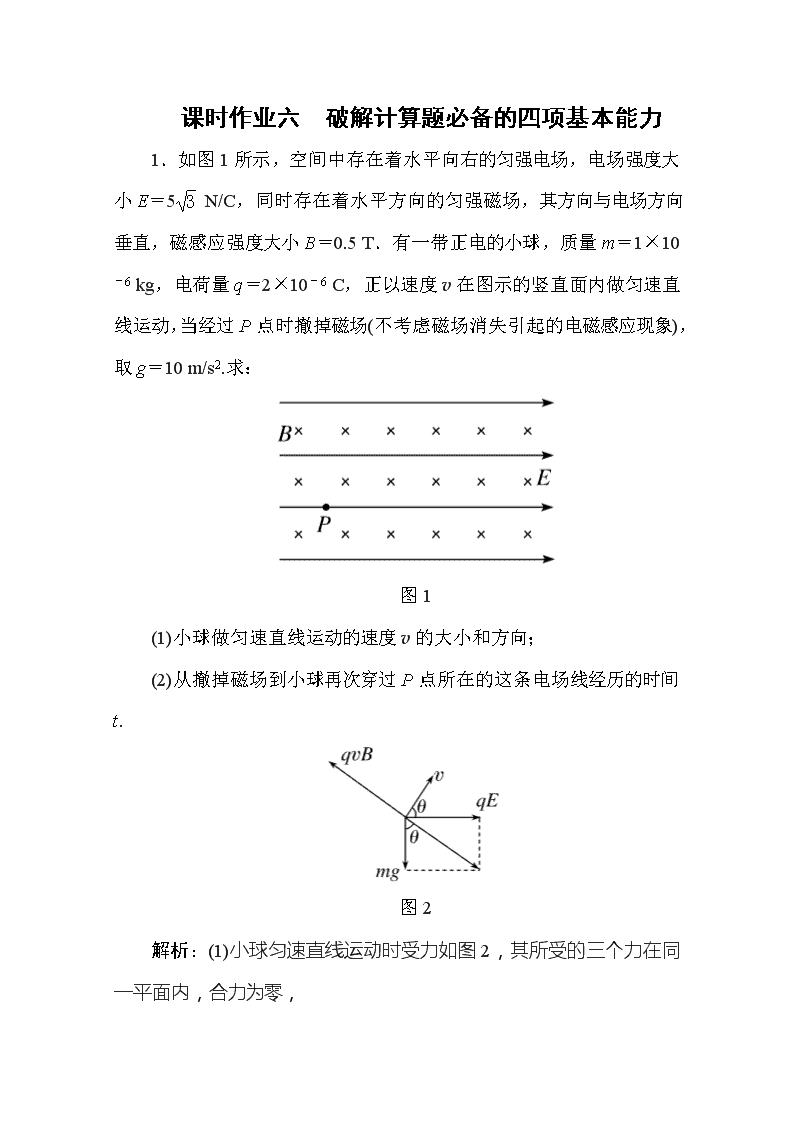
课时作业六　破解计算题必备的四项基本能力 ‎1．如图1所示，空间中存在着水平向右的匀强电场，电场强度大小E＝5 N/C，同时存在着水平方向的匀强磁场，其方向与电场方向垂直，磁感应强度大小B＝0.5 T．有一带正电的小球，质量m＝1×10－6 kg，电荷量q＝2×10－6 C，正以速度v在图示的竖直面内做匀速直线运动，当经过P点时撤掉磁场(不考虑磁场消失引起的电磁感应现象)，取g＝10 m/s2.求：‎ 图1‎ ‎(1)小球做匀速直线运动的速度v的大小和方向；‎ ‎(2)从撤掉磁场到小球再次穿过P点所在的这条电场线经历的时间t.‎ 图2‎ 解析：(1)小球匀速直线运动时受力如图2，其所受的三个力在同一平面内，合力为零，‎ 有qvB＝ 代入数据解得 v＝20 m/s 速度v的方向与电场E的方向之间的夹角θ满足 tanθ＝，代入数据解得tanθ＝，‎ θ＝60°.‎ ‎(2)撤去磁场后，由于电场力垂直于竖直方向，它对竖直方向的分运动没有影响，以P点为坐标原点，竖直向上为正方向，小球在竖直方向上做匀减速运动，其初速度为vy＝vsinθ，若使小球再次穿过P点所在的电场线，仅需小球的竖直方向的分位移为零，则有vyt－gt2＝0，联立解得 t＝2 s≈3.5 s.‎ 答案：(1)20 m/s，方向与电场方向成60°角斜向上 ‎(2)3.5 s ‎2．回旋加速器的工作原理如图3甲所示，置于真空中的D形金属盒半径为R.两盒间狭缝的间距为d，磁感应强度为B的匀强磁场与盒面垂直．被加速粒子的质量为m、电荷量为＋q，加在狭缝间的交变电压如图3乙所示，电压值的大小为U0，周期T＝.一束该种粒子在t＝0～时间内从A处均匀地飘入狭缝，其初速度视为零．现考虑粒子在狭缝中的运动时间，假设能够出射的粒子每次经过狭缝均做加速运动，‎ 不考虑粒子间的相互作用．求：‎ ‎ 　‎ 甲 乙 图3‎ ‎(1)出射粒子的动能Em；‎ ‎(2)粒子从飘入狭缝至动能达到Em所需的总时间t0；‎ ‎(3)要使飘入狭缝的粒子中有超过99%能射出，d应满足的条件．‎ 解析：(1)粒子运动半径为R时，qvB＝m，‎ 且Em＝mv2，解得Em＝.‎ ‎(2)粒子被加速n次达到动能Em，则Em＝nqU0‎ 粒子在狭缝间做匀加速运动，‎ 设n次经过狭缝的总时间为Δt 加速度a＝ 匀加速直线运动nd＝a·Δt2‎ 由t0＝(n－1)·＋Δt，‎ 解得t0＝－.‎ ‎(3)只有在0～(－Δt)时间内飘入的粒子才能每次均被加速 则所占的比例为η＝ 由η＞99%，解得d＜.‎ 答案：(1)　(2)－ ‎(3)d< ‎3．轻质弹簧原长为2l，将弹簧竖直放置在地面上，在其顶端将一质量为5m的物体由静止释放，当弹簧被压缩到最短时，弹簧长度为l.现将该弹簧水平放置，一端固定在A点，另一端与物块P接触但不连接．AB是长度为5l的水平轨道，B端与半径为l的光滑半圆轨道BCD相切，半圆的直径BD竖直，如图4乙所示．物块P与AB间的动摩擦因数μ＝0.5.用外力推动物块P，将弹簧压缩至长度l，然后放开，P开始沿轨道运动．重力加速度大小为g.‎ 图4‎ ‎(1)若P的质量为m，求P到达B点时速度的大小，以及它离开圆轨道后落回到AB上的位置与B点之间的距离；‎ ‎(2)若P能滑上圆轨道，且仍能沿圆轨道滑下，求P的质量的取值范围．‎ 解析：(1)依题意，当弹簧竖直放置，长度被压缩至l时，质量为5m 的物体的动能为零，其重力势能转化为弹簧的弹性势能．‎ 由机械能守恒定律，弹簧长度为l时的弹性势能为 Ep＝5mgl①‎ 设P的质量为M，到达B点时的速度大小为vB，‎ 由能量守恒定律得 Ep＝MvB2＋μMg·4l②‎ 联立①②式，取M＝m并代入题给数据得 vB＝③‎ 若P能沿圆轨道运动到D点，其到达D点时的向心力不能小于重力，即P此时的速度大小v应满足 －mg≥0④‎ 设P滑到D点时的速度为vD，由机械能守恒定律得 mvB2＝mvD2＋mg·2l⑤‎ 联立③⑤式得vD＝⑥‎ vD满足④式要求，故P能运动到D点，并从D点以速度vD水平射出．设P落回到轨道AB所需的时间为t，‎ 由运动学公式得2l＝gt2⑦‎ P落回到AB上的位置与B点之间的距离为 s＝vDt⑧‎ 联立⑥⑦⑧式得s＝2l.⑨‎ ‎(2)为使P能滑上圆轨道，它到达B点时的速度不能小于零．由①②式可知5mgl＞μMg·4l⑩‎ 要使P仍能沿圆轨道滑回，P在圆轨道的上升高度不能超过半圆轨道的中点C.‎ 由机械能守恒定律有MvB2≤Mgl⑪‎ 联立①②⑩⑪式得 ‎ m≤M

查看更多