【物理】2020届二轮复习电场和磁场中的曲线运动作业

【物理】2020届二轮复习电场和磁场中的曲线运动作业

课时作业4　电场和磁场中的曲线运动 一、选择题(1～6题为单项选择题，7、8题为多项选择题)‎ ‎1.‎ 如图所示，在竖直向上的匀强电场中，一根不可伸长的绝缘细绳的一端系着一个带电小球，另一端固定于O点，小球在竖直平面内做匀速圆周运动，最高点为a，最低点为b.不计空气阻力，则下列说法正确的是(　　)‎ A．小球带负电 B．电场力跟重力平衡 C．小球在从a点运动到b点的过程中，电势能减小 D．小球在运动过程中机械能守恒 解析：由于小球在竖直平面内做匀速圆周运动，所以重力与电场力的合力为0，电场力方向竖直向上，小球带正电，A错，B对；从a→b，电场力做负功，电势能增大，C错；由于有电场力做功，机械能不守恒，D错．‎ 答案：B ‎2.‎ 如图所示，在圆形区域内，存在垂直纸面向外的匀强磁场，ab是圆的一条直径．一带电粒子从a点射入磁场，速度大小为2v，方向与ab成30°时恰好从b点飞出磁场，粒子在磁场中运动的时间为t；若仅将入射速度大小改为v，则粒子在磁场中运动的时间为(不计带电粒子所受重力)(　　)‎ A．3t B.t C.t D．2t 解析：由洛伦兹力提供向心力得Bqv＝m＝mR，化简得R＝ ‎，T＝；粒子以2v的速度从a射入、b点射出得到划过圆弧的圆心角为60°，由R＝得，当粒子以速度v入射时，粒子运动轨迹半径变为原来的一半，划过的圆弧所对的圆心角变为120°，由T＝得，两次粒子运动的周期不变，所以粒子在磁场中运动的时间变为2t，故D项正确．‎ 答案：D ‎3.‎ ‎[2019·安徽蚌埠四校联考]如图所示，两极板与电源相连接，电子从负极板边缘沿垂直电场方向射入匀强电场，电子恰好从正极板边缘飞出，现保持负极板不动，正极板在竖直方向移动，并使电子入射速度变为原来的2倍，而电子仍从原位置射入，且仍从正极板边缘飞出，则两极板间距离变为原来的(　　)‎ A．2倍 B．4倍 C. D. 解析：电子从负极板边缘垂直电场方向射入匀强电场，做类平抛运动．假设电子的带电荷量为e，质量为m，初速度为v，极板的长度为L，极板的间距为d，电场强度为E.由于电子做类平抛运动，所以水平方向有：L＝vt，竖直方向有：y＝at2＝··2＝d.因为E＝，可得：d2＝，若电子的速度变为原来的两倍，仍从正极板边缘飞出，则由上式可得两极板的间距d应变为原来的，故选C.‎ 答案：C ‎4．如图所示，在直角三角形abc区域(含边界)内存在垂直于纸面向外的匀强磁场，磁感应强度大小为B，∠a＝60°，∠b＝90°，边长ac＝L.一个粒子源在a点将质量为m、电荷量为q的带正电粒子以大小和方向不同的速度射入磁场，在磁场中运动时间最长的粒子中，速度的最大值是(　　)‎ A. B. C. D. 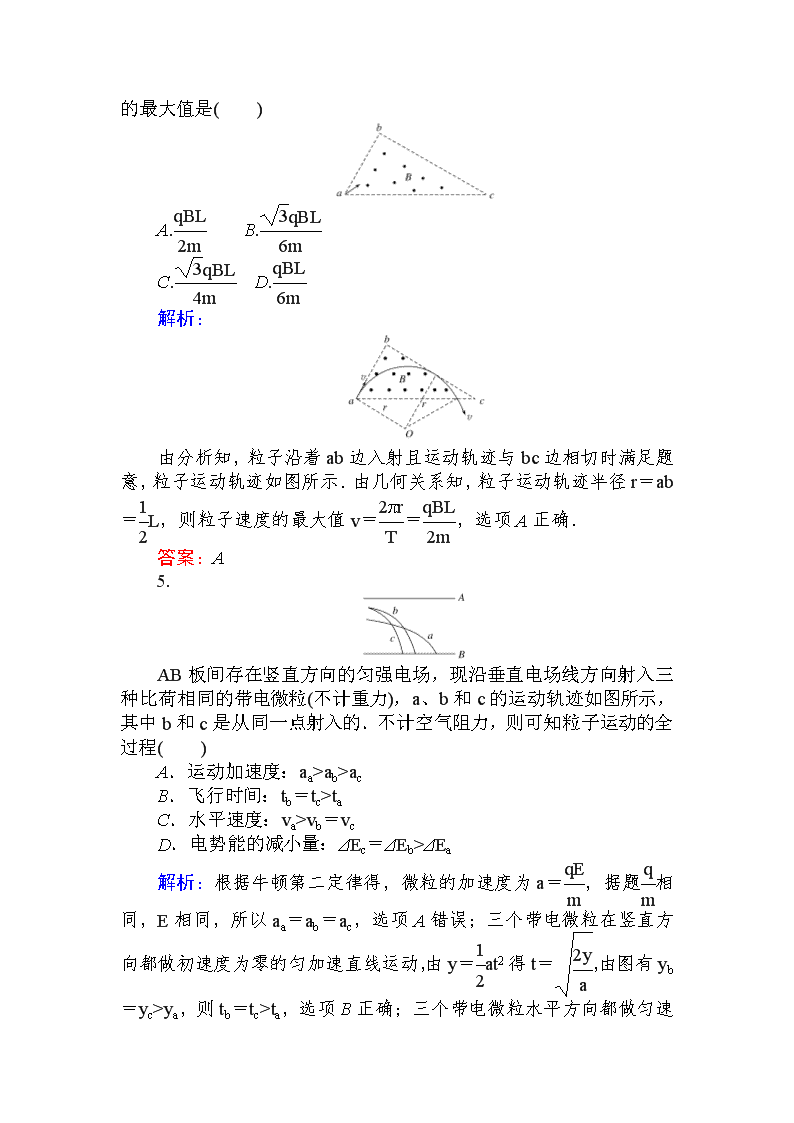解析：‎ 由分析知，粒子沿着ab边入射且运动轨迹与bc边相切时满足题意，粒子运动轨迹如图所示．由几何关系知，粒子运动轨迹半径r＝ab＝L，则粒子速度的最大值v＝＝，选项A正确．‎ 答案：A ‎5.‎ AB板间存在竖直方向的匀强电场，现沿垂直电场线方向射入三种比荷相同的带电微粒(不计重力)，a、b和c的运动轨迹如图所示，其中b和c是从同一点射入的．不计空气阻力，则可知粒子运动的全过程(　　)‎ A．运动加速度：aa>ab>ac B．飞行时间：tb＝tc>ta C．水平速度：va>vb＝vc D．电势能的减小量：ΔEc＝ΔEb>ΔEa 解析：根据牛顿第二定律得，微粒的加速度为a＝，据题相同，E相同，所以aa＝ab＝ac，选项A错误；三个带电微粒在竖直方向都做初速度为零的匀加速直线运动，由y＝at2得t＝，由图有yb＝yc>ya，则tb＝tc>ta，选项B正确；三个带电微粒水平方向都做匀速直线运动，由x＝v0t得v0＝，由图知xa>xb>xc，又tb＝tc>ta，则va>vb ‎>vc，选项C错误；电场力做功为W＝qEy，由于三个微粒的电荷量关系不能确定，所以不能确定电场力做功的大小，也就不能确定电势能减少量的大小，选项D错误．‎ 答案：B ‎6.‎ 如图所示，水平放置的平行板长度为L、两板间距也为L，两板之间存在垂直纸面向里、磁感应强度大小为B的匀强磁场，在两板正中央P点有一个不计重力的电子(质量为m、电荷量为－e)，现在给电子一水平向右的瞬时初速度v0，欲使电子不与平行板相碰撞，则(　　)‎ A．v0>或v0< B. D．v0< 解析：‎ 此题疑难点在于确定“不与平行板相碰撞”的临界条件．电子在磁场中做匀速圆周运动，半径为R＝，如图所示．当R1＝时，电子恰好与下板相切；当R2＝时，电子恰好从下板边缘飞出两平行板(即飞出磁场)．由R1＝，解得v1＝，由R2＝，解得v2＝，所以欲使电子不与平行板相碰撞，电子初速度v0应满足v0>或v0<，故选项A正确．‎ 答案：A ‎7.‎ 如图，一粒子发射源P位于足够长绝缘板AB的上方d处，能够在纸面内向各个方向发射速率为v、比荷为k的带正电的粒子，空间存在垂直纸面的匀强磁场，不考虑粒子间的相互作用和粒子重力．已知粒子做圆周运动的半径大小恰好为d，则(　　)‎ A．磁感应强度的大小为 B．磁感应强度的大小为 C．同一时刻发射出的带电粒子打到板上的最大时间差为 D．同一时刻发射出的带电粒子打到板上的最大时间差为 解析：‎ 根据qvB＝m和R＝d、＝k得B＝，选项A错误，B正确；能打到板上的粒子中，在磁场中运动时间最长和最短的运动轨迹示意图如图所示，由几何关系，最长时间t1＝T，最短时间t2＝T，T＝，所以最大时间差Δt＝t1－t2＝T＝，选项C正确，D错误．‎ 答案：BC ‎8.‎ ‎[2019·浙江卷，13改编]用长为‎1.4 m的轻质柔软绝缘细线，拴一质量为1.0×10－‎2 kg、电荷量为2.0×10－‎8 C的小球，细线的上端固定于O点．现加一水平向右的匀强电场，平衡时细线与铅垂线成37°角，如图所示．现向左拉小球使细线水平且拉直，静止释放，则(sin 37°＝0.6)(　　)‎ A．该匀强电场的场强为3.75×106 N/C B．平衡时细线的拉力为0.17 N C．经过0.5 s，小球的速度大小为‎6.25 m/s D．小球第一次通过O点正下方时，速度大小为‎7 m/s 解析：‎ 小球处于平衡状态时，受力分析如图所示，则可知qE＝mgtan 37°，则该匀强电场的电场强度E＝＝3.75×106 N/C，A正确；细线的拉力F＝＝0.125 N，故B错误；在外力作用下，小球拉至细线水平时，由静止释放，如图所示，小球在电场力和重力的作用下，从A点由静止开始做匀加速直线运动至B点，∠OAB＝∠OBA＝53°，OA＝OB＝l＝‎1.4 m，在此过程中，细线处于松弛状态，无拉力作用，小球运动至B点时，细线绷紧，匀加速直线运动结束．根据牛顿第二定律可知小球匀加速直线运动时的加速度a＝＝＝ m/s2＝‎12.5 m/s2，假设经过0.5 s后，小球仍在沿AB方向做匀加速直线运动，则小球的速度v＝at＝‎6.25 m/s，经过的距离x＝at2＝×12.5×‎0.52 m＝1.562 ‎5 m，A、B间的距离|AB|＝2×l×cos 53°＝‎1.68 m，x<|AB|，假设成立，故0.5 s时，小球的速度大小为‎6.25 m/s，故C正确；小球运动至B点时，细线绷紧，小球沿细线方向的分速度减为零，动能减小，假设细线绷紧过程小球机械能损失ΔE，此后在电场力、重力和细线拉力作用下沿圆弧运动至O点正下方，根据能量守恒定律，可知(qE＋mg)·l－ΔE＝mv2，可得v>‎7 m/s，故D错误．‎ 答案：AC 易错点拨：本题易错选D.小球从A点运动至最低点的过程中可分成两个过程，前一过程做匀加速直线运动，后一过程做圆周运动，速度沿圆弧切线方向．经过B点时，细线绷紧，绷紧前的速度方向并不是绷紧后速度方向，绷紧瞬间发生速度的变化，机械能损失，故小球在最低点时v<‎7 m/s.‎ 二、非选择题 ‎9.‎ 如图所示，有一平面直角坐标系xOy，其中x轴的正方向为水平向右，y轴的正方向为竖直向上．在x>0的空间中，存在沿x轴正方向的匀强电场；在x<0的空间中，存在沿x轴负方向的匀强电场，电场强度大小均为E＝1 N/C.一质量m＝‎10 g、电荷量q＝‎0.1 C的带负电的小球在点P(‎10 cm,0)处由静止释放，不计空气阻力，(重力加速度g＝‎10 m/s2)求：‎ ‎(1)小球第一次到达y轴时的速度；‎ ‎(2)小球第二次到达y轴时的位置坐标．‎ 解析：(1)小球在P点时，对小球受力分析可知：‎ 所受电场力水平向左，大小为F电＝qE＝0.1 N 所受重力竖直向下，大小为G＝mg＝0.1 N 所以小球受到的合力斜向左下方，与x轴的负方向的夹角为45°，大小为F＝ N 由牛顿第二定律和运动学公式可知，小球在x>0的空间运动的加速度大小为：a＝ 设小球第一次到达y轴上的点为A，‎ 则v＝2alPA，其中lPA＝xP 解得小球到达A点的速度为v1＝‎2 m/s ‎(2)‎ 小球在x<0的空间运动时受合力的大小仍为F、方向斜向右下方，与y轴负方向的夹角为45°，所以小球在x<0的空间内以大小为a的加速度做类平抛运动，小球从A运动到B的过程中，在合力的方向与合力垂直的方向运动的位移大小相等，则有 v1t＝at2＝l l＝lAB 解得：lAB＝‎‎80 cm 由几何关系可知lOA＝‎‎10 cm 所以小球第二次到达y轴的坐标为(0，－‎90 cm)‎ 答案：(1)‎2 m/s　(2)(0，－‎90 cm)‎ ‎10.‎ ‎[2019·河南省开封市三模]如图所示，在直角坐标系xOy的第一象限中有两个全等的直角三角形区域Ⅰ和Ⅱ，充满了方向均垂直纸面向里的匀强磁场，区域Ⅰ的磁感应强度大小为B0，区域Ⅱ的磁感应强度大小可调，C点坐标为 ‎(‎4L,‎3L)，M点为OC的中点．质量为m、电荷量为－q(q>0)的粒子从C点以平行于y轴方向射入磁场Ⅱ中，速度大小为，不计粒子所受重力，粒子运动轨迹与磁场区域相切时认为粒子能再次进入磁场．‎ ‎(1)若粒子无法进入区域Ⅰ中，求区域Ⅱ磁感应强度大小范围；‎ ‎(2)若粒子恰好不能从AC边射出，求区域Ⅱ磁感应强度大小．‎ 解析：(1)如图甲所示，当运动轨迹与x轴相切时，粒子恰好能进入区域Ⅰ中．由几何关系可知粒子圆周运动半径为r＝‎3L，v＝，‎ 由qvB＝m得B＝ 若粒子无法进入区域Ⅰ中，‎ 则r>‎3L，区域Ⅱ磁感应强度B<.‎ ‎(2)若粒子恰好不能从AC边射出，粒子轨迹与AC边相切于E点，运动轨迹如图乙所示，由几何关系可知∠O2O1E＝2θ，粒子在磁场Ⅰ中，qvB0＝m，v＝，可得粒子在磁场Ⅰ中轨道半径为r1＝.‎ 设在磁场Ⅱ中的轨道半径为R，由几何关系可知，R＝r1＋ 由sin θ＝可知sin 2θ＝，解得R＝L 在磁场Ⅱ中由qvB＝m，v＝，可知B＝.‎ 答案：(1)B<　(2)