法拉第电磁感应定律教案(3)

法拉第电磁感应定律教案(3)

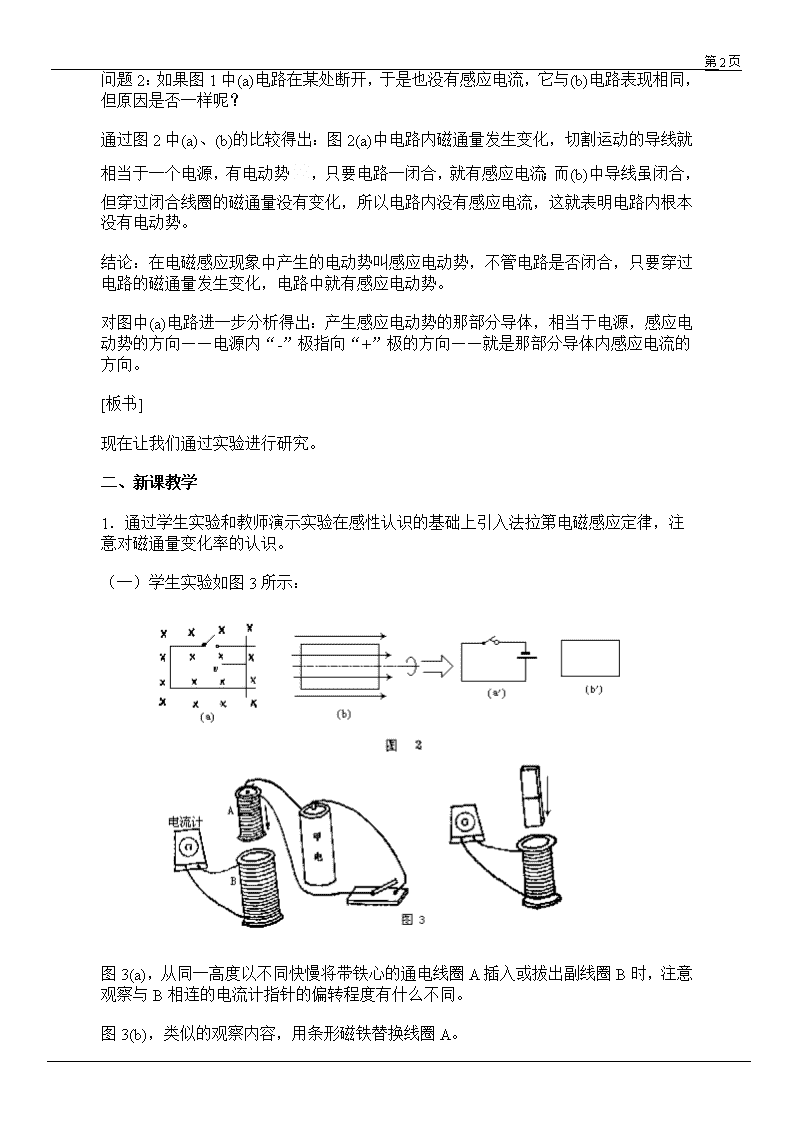
第 1 页 法拉第电磁感应定律的教案 　 教学目的 1．理解电磁感应现象里感应电动势的存在，并能判断其方向。 2．在实验的基础上掌握法拉第电磁感应定律，并使学生体会在发现和认识物理规律 中物理实验的重要作用，培养学生在物理实验中仔细观察和认真思考的能力。 教具 大型示教万用电表、圆柱形空心线圈、条形磁铁、蹄形磁铁、自制矩形线圈、木架等。 教学过程 一、复习提问，过渡新课 上节课已学习了在闭合电路中产生感应电流的条件，但感应电流的大小怎样计算还不 知道。这节课将通过实验进一步研究电磁感应现象，学会如何计算磁通量变化率的问 题。 先复习提问，目的有二： 1．着重明确产生电磁感应现象的条件是穿过回路的磁通量发生变化； 2．明确发生电磁感应现象时一定会产生感应电动势，但不一定产生感应电流； 问题 1：闭合电路中产生感应电流的条件是什么？判断下列电路中是否有感应电流？ 图 1(a)ABCD 为导线框，AB 为可动部分；(b)中线圈 ABCD 绕 OO′转动，OO′平行 于磁感线。 要求学生明确“闭合电路中产生感应电流的条件是穿过闭合电路的磁通量发生变化” 以此得出(a)中有感应电流。 在(b)中，穿过闭合电路的磁通量始终为零，没有发生变化，所以没有感应电流。 第 2 页 问题 2：如果图 1 中(a)电路在某处断开，于是也没有感应电流，它与(b)电路表现相同， 但原因是否一样呢？ 通过图 2 中(a)、(b)的比较得出：图 2(a)中电路内磁通量发生变化，切割运动的导线就 相当于一个电源，有电动势 ，只要电路一闭合，就有感应电流；而(b)中导线虽闭合， 但穿过闭合线圈的磁通量没有变化，所以电路内没有感应电流，这就表明电路内根本 没有电动势。 结论：在电磁感应现象中产生的电动势叫感应电动势，不管电路是否闭合，只要穿过 电路的磁通量发生变化，电路中就有感应电动势。 对图中(a)电路进一步分析得出：产生感应电动势的那部分导体，相当于电源，感应电 动势的方向——电源内“-”极指向“+”极的方向——就是那部分导体内感应电流的 方向。 [板书] 现在让我们通过实验进行研究。 二、新课教学 1．通过学生实验和教师演示实验在感性认识的基础上引入法拉第电磁感应定律，注 意对磁通量变化率的认识。 （一）学生实验如图 3 所示： 图 3(a)，从同一高度以不同快慢将带铁心的通电线圈 A 插入或拔出副线圈 B 时，注意 观察与 B 相连的电流计指针的偏转程度有什么不同。 图 3(b)，类似的观察内容，用条形磁铁替换线圈 A。 第 3 页 上述实验要求学生在五分钟内完成。并提醒学生做毕及时打开电键。 请一位学生将自己观察到的现象叙述一下，再问一问全班同学是否都观察到同样的现 象？ (若以不同的速度：非常慢地、较快地、很快地插入和拔出副线圈 B 时，电流计上指 针偏转程度有明显的差异：从 20μA 到超过 300μA；插入或拔出得越快，指针偏转 越大，) （二）教师演示如图 4，请全体学生共同观察电流表指针偏转程度与什么有关？ 图 4(a)与学生实验同，图 4(b)是闭合线圈中部分导线以不同的速度切割磁感线。 （三）要求学生思考三个问题后得出实验结论。 问题 1：在所做的实验中，电流表指针发生偏转的共同原因是什么？ 穿过电路的磁通量发生变化，电路中有感应电动势，电路闭合产生感应电流。 问题 2：观察电流表指针的偏转程度与研究感应电动势的大小有什么关系？ 问题 3：用不同的快慢将磁铁从同一高度全部插入线圈内，穿过线圈的磁通量的变化 情况有什么相同和不同？ 请学生归纳总结感应电动势的大小与磁通量变化情况有怎样的关系？ 第 4 页 （四）法拉第电磁感应定律。 [板书] 教师指出精确的实验表明，电路中感应电动势的大小，跟穿过这一电路的磁通量的变 化率成正比。 首先对这个问题进行实验研究的是英国的实验物理学家法拉第，因此人们把这个定律 称作法拉第电磁感应定律。 (1)在国际单位制中，ε 用“伏特”做单位，φ 用“韦伯”做单位，t 用“秒”做单位 时，实验测量或理论推导都表明 K 值正好等于 1．所以 2．在法拉第电磁感应定律的应用中导出 ε=Blvsinθ 进一步提出问题：弧立的一根导线作切割磁感线运动时，导线上产生的感应电动势又 如何计算呢？ 向学生指出，这个计算式我们只在一定的条件下进行推导。 第 5 页 推导 1 条件：“三垂直”，即磁感应强度 B、导线切割速度 v 、和长为 l 的导线本身 三者之间互相都垂直，如图 5(a)。请全体学生推导导线 AB 上感应电动势 ε 的计算式， 教师启发指导：让学生将图 5(a)与图 2(a)进行比较，并可作板图进行引导(图 5(b))。 推导 2 条件：上述三垂直中只有二垂直，而 v 与 B 不垂直，设夹角为 θ，再请全体学 生推导 E 的计算式。教师指点方法：将 v 分解，其中与磁感线平行的速度分量没有作 用，有效切割速度为 vsinθ(图 6)，因此得： ε=Blvsinθ (5)[板书] 指出(5)式中当 θ=90°时，ε=Blvsin90°=Blv 可见公式(5)比公式(4)更有普遍意义。 指出公式(4)、(5)的单位都采用国际单位制。 三、例题 图 7 中 A、B 两线圈面积相同，都是 0.6m2．圈数都是 10 匝，分别处在两个变化的均 匀磁场中，B1 在 0.1s 由 0 均匀增加到 0.04T 后不变，B2 在 0.2s 由 0 均匀增加到 0.06T 后不变。请学生鉴别：在 φ-t、E-t 图象中图线(1)、(2)、(3)、(4)各属于哪个线圈？并 计算图象中：φ1=？φ2=？；E1=？E2=？(注：A 线圈边长：0.78m B 线圈半径：0.44m) 第 6 页 解：φA=B1S=0.04×0.6=0.024(wb) φB=BS=0.06×0.6=0.036(wb) 磁场变化过程中： 答：(1)、(4)属于 A 线圈，φ1=0.024Wb，E2=2.4V (2)、(3)属于 B 线圈，φ2=0.036Wb，E1=1.8V 书上例题让学生自己阅读。 四、小结 第 7 页 ε=Blvsinθ 是在“二垂直”的条件下，导线切割磁感线时感应电动势的计算式。 二个公式是一致的，可以互相推导，两个公式应用时单位都要采用国际单位制。 从二个公式中也可说明感应电动势只与产生电磁感应现象的条件有关，它是反映电磁 感应现象本质的物理量。 感应电动势的方向，是指相当于电源的这一部分“内电路”中从负极指向正极的方向， 即与内电路中感应电流的方向一致。 五、布置作业