【物理】2019届一轮复习人教版法拉第电磁感应定律的应用学案

【物理】2019届一轮复习人教版法拉第电磁感应定律的应用学案

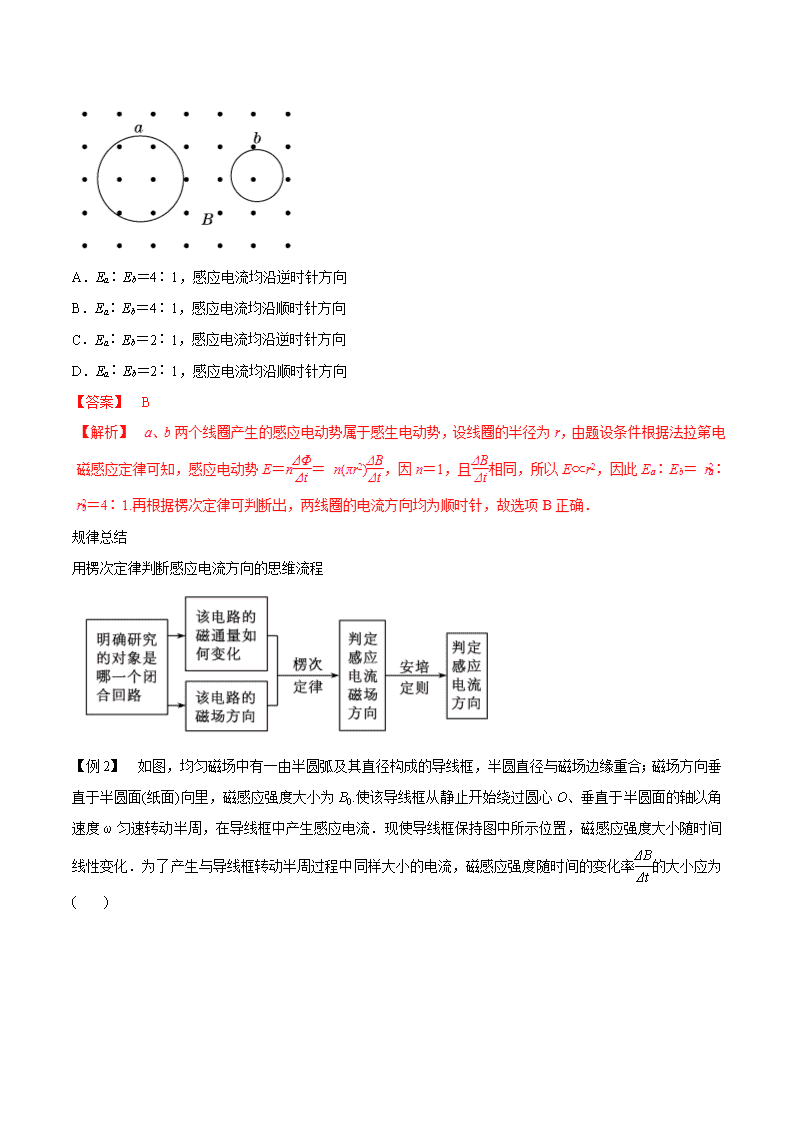
知识回顾 1．“三定则、一定律”的应用 (1)安培定则：判断运动电荷、电流产生的磁场方向． (2)左手定则：判断磁场对运动电荷、电流的作用力的方向． (3)右手定则：判断部分导体切割磁感线产生感应电流的方向． (4)楞次定律：判断闭合电路磁通量发生变化产生感应电流的方向． 2．求感应电动势的两种方法 (1)E＝nΔΦ Δt ，用来计算感应电动势的平均值． (2)E＝BLv，主要用来计算感应电动势的瞬时值． (3)E＝1 2BL2ω 用来计算转动切割产生的电动势． 规律方法 1．感应电流方向的判断方法 一是利用右手定则，即根据导体在磁场中做切割磁感线运动的情况进行判断； 二是利用楞次定律，即根据穿过回路的磁通量的变化情况进行判断． 2．楞次定律中“阻碍”的主要表现形式 (1)阻碍原磁通量的变化——“增反减同”； (2)阻碍相对运动——“来拒去留”； (3)使线圈面积有扩大或缩小的趋势——“增缩减扩”； (4)阻碍原电流的变化(自感现象)——“增反减同”． 3．在应用法拉第电磁感应定律 E＝nΔΦ Δt ＝n ΔBS Δt 时要注意的事项 S 为有效面积，当线圈的面积大于磁场的区域时，一般磁场的面积为有效面积． 例题分析 【例 1】　(2016 年高考·北京卷)如图所示，匀强磁场中有两个导体圆环 a、b，磁场方向与圆环所在平面垂 直．磁感应强度 B 随时间均匀增大．两圆环半径之比为 2∶1，圆环中产生的感应电动势分别为 Ea 和 Eb.不 考虑两圆环间的相互影响．下列说法正确的是(　　) A．Ea∶Eb＝4∶1，感应电流均沿逆时针方向 B．Ea∶Eb＝4∶1，感应电流均沿顺时针方向 C．Ea∶Eb＝2∶1，感应电流均沿逆时针方向 D．Ea∶Eb＝2∶1，感应电流均沿顺时针方向 【答案】　B 规律总结 用楞次定律判断感应电流方向的思维流程 【例 2】　如图，均匀磁场中有一由半圆弧及其直径构成的导线框，半圆直径与磁场边缘重合；磁场方向垂 直于半圆面(纸面)向里，磁感应强度大小为 B0.使该导线框从静止开始绕过圆心 O、垂直于半圆面的轴以角 速度 ω 匀速转动半周，在导线框中产生感应电流．现使导线框保持图中所示位置，磁感应强度大小随时间 线性变化．为了产生与导线框转动半周过程中同样大小的电流，磁感应强度随时间的变化率ΔB Δt 的大小应为 (　　) A.4ωB0 π B.2ωB0 π C.ωB0 π D.ωB0 2π 【答案】　C 【例 3】　(2017 年广东省两校二模)如图所示，一横截面积为 S 的 n 匝线圈，与相距为 d 的两块水平放置的 平行金属板连接成电路．线圈置于方向竖直向上的匀强磁场中，为使一质量为 m，电荷量为＋q 的小球在平 行金属板间水平向右做直线运动，重力加速度为 g，则磁感应强度的变化情况应为(　　) A．正在增强，ΔB Δt ＝mgd nSq B．正在减弱，ΔB Δt ＝mgd nSq C．正在增强，ΔB Δt ＝mgd 2nSq D．正在减弱，ΔB Δt ＝mgd 2nSq 【答案】　B 【解析】　小球做直线运动，则重力和电场力平衡，所以 q·U d＝mg，由于小球带正电，电场力向下，所以 上极板带负电，由楞次定律知磁场强度正在减弱，由法拉第电磁感应定律 U＝n·ΔΦ Δt ，ΔΦ＝ΔBS，所以ΔB Δt ＝mgd nSq， 故 B 正确．学 专题练习 1. (2017 年北京海淀区期末)如图所示，左侧闭合电路中的电流大小为 I1，ab 为一段长直导线．右侧平行金 属导轨的左端连接有与 ab 平行的长直导线 cd，在远离 cd 导线的右侧空间存在与导轨垂直的匀强磁场，在 磁场区域放置垂直导轨且与导轨接触良好的导体棒 MN，当导体棒沿导轨匀速运动时，可以在 cd 上产生大 小为 I2 的感应电流．已知 I1>I2，不计匀强磁场对导线 ab 和 cd 的作用．用 F1 和 F2 分别表示导线 cd 对 ab 的 安培力大小和导线 ab 对 cd 的安培力大小，下列说法正确的是(　　) A．若 MN 向左运动，ab 与 cd 两导线相互吸引，F1＝F2 B．若 MN 向右运动，ab 与 cd 两导线相互吸引，F1＝F2 C．若 MN 向左运动，ab 与 cd 两导线相互吸引，F1>F2 D．若 MN 向右运动，ab 与 cd 两导线相互吸引，F1>F2 【答案】：B 2．(多选)(2016 年高考·上海卷)如图 (a)，螺线管内有平行于轴线的外加匀强磁场，以图中箭头所示方向为 其正方向．螺线管与导线框 abcd 相连，导线框内有一小金属圆环 L，圆环与导线框在同一平面内．当螺线 管内的磁感应强度 B 随时间按图 (b)所示规律变化时(　　) A．在 t1 t2 时间内，L 有收缩趋势 B．在 t2 t3 时间内，L 有扩张趋势 C．在 t2 t3 时间内，L 内有逆时针方向的感应电流 D．在 t3 t4 时间内，L 内有顺时针方向的感应电流 【答案】：AD 3．(多选)(2017 年河南六市一模)如图所示，在边长为 a 的等边三角形区域内有匀强磁场 B，其方向垂直于 纸面向外，一个边长也为 a 的等边三角形导线框架 EFG 正好与上述磁场区域的边界重合，而后绕其几何中 心 O 点在纸面内以角速度 ω 顺时针方向匀速转动，于是框架 EFG 中产生感应电动势，若转过 60°后线框转 到图中的虚线位置，则在这段时间内(　　) A．感应电流方向为 E→G→F→E B．感应电流方向为 E→F→G→E C．平均感应电动势大小等于 3ωa2B 4π D．平均感应电动势大小等于 3ωa2B 3π 【答案】：BC 4. (多选)(2017 年湖北名校联考)如图所示，把电阻 R、电感线圈 L、电容器 C 并联，三个支路中分别接一灯 泡，接入交流电源后，三盏灯亮度相同．若保持交流电源的电压不变，使交变电流的频率增大，则(　　) A．与线圈 L 连接的灯泡 L1 将变暗 B．与电容器 C 连接的灯泡 L2 将变亮 C．与电阻 R 连接的灯泡 L3 将变暗 D．三盏灯泡的亮度都不会改变 【答案】：AB 【解析】：当交变电流的频率增大时，对 R 无影响，L3 亮度不变，电感线圈感抗增大，L1 变暗，电容器容 抗减小，则灯泡 L2 变亮，故 A、B 正确． 5．如图所示，足够长的 U 形光滑金属导轨所在平面与水平面成 θ 角(0＜θ＜90°)，其中 MN 与 PQ 平行且间 距为 L，磁感应强度大小为 B 的匀强磁场方向垂直导轨所在平面斜向上，导轨电阻不计，金属棒 ab 由静止 开始沿导轨下滑，并与两导轨始终保持垂直且接触良好，棒 ab 接入电路的电阻为 R，当流过棒 ab 某一横截 面的电荷量为 q 时，棒的速度大小为 v，则金属棒 ab 在下滑过程中 (　　) A．运动的加速度大小为v2 2L B．下滑位移大小为qR BL C．产生的焦耳热为 qBLv D．受到的最大安培力大小为 B2L2v R sin θ 【答案】　B 6．(沈阳市三模，21)如图甲所示，电阻不计且间距 L＝1 m 的光滑平行金属导轨竖直放置，上端接一阻值 R ＝2 Ω 的电阻，虚线 OO′下方有垂直于导轨平面向里的匀强磁场，现将质量 m＝0.1 kg、电阻不计的金属杆 ab 从 OO′上方某处由静止释放，金属杆在下落的过程中与导轨保持良好接触且始终水平，已知杆 ab 进入磁场 时的速度 v0＝1 m/s，下落 0.3 m 的过程中加速度 a 与下落距离 h 的关系图象如图乙所示，g 取 10 m/s2，则 (　　) A．匀强磁场的磁感应强度为 1 T B．杆 ab 下落 0.3 m 时金属杆的速度为 1 m/s C．杆 ab 下落 0.3 m 的过程中 R 上产生的热量为 0.2 J D．杆 ab 下落 0.3 m 的过程中通过 R 的电荷量为 0.25 C 【答案】　D 【解析】　在杆 ab 进入磁场时，由B2L2v0 R －mg＝ma，由题图乙知，a 的大小为 10 m/s2，解得 B＝2 T，A 错 误．杆 ab 下落 0.3 m 时杆做匀速运动，则有B2L2v′ R ＝mg，解得 v′＝0.5 m/s，选项 B 错误，在杆 ab 下落 0.3 m 的过程，根据能量守恒，R 上产生的热量为 Q＝mgh－1 2mv′2＝0.287 5 J，选项 C 错误．通过 R 的电荷量 q＝ ΔΦ R ＝B·ΔS R ＝0.25 C．选项 D 正确．学 7．垂直斜面的磁场宽度均为 L，一质量为 m、电阻为 R、边长为L 2的正方形导体线圈，在沿平行斜面向下的 拉力 F 作用下由静止开始沿斜面下滑，当 ab 边刚越过 GH 进入磁场Ⅰ时，恰好做匀速直线运动，下列说法 中正确的有(重力加速度为 g) (　　) A．从线圈的 ab 边刚进入磁场Ⅰ到线圈 dc 边刚要离开磁场Ⅱ的过程中，线圈 ab 边中产生的感应电流先沿 b→a 方向再沿 a→b 方向 B．线圈进入磁场Ⅰ过程和离开磁场Ⅱ过程所受安培力方向都平行斜面向上 C．线圈 ab 边刚进入磁场Ⅰ时的速度大小为4Rmgsin θ＋F B2L2 D．线圈进入磁场Ⅰ做匀速运动的过程中，拉力 F 所做的功等于线圈克服安培力所做的功 【答案】　BC 8．如图所示，在竖直向下的 y 轴两侧分布有垂直纸面向外和向里的磁场，磁感应强度大小 B 均随 y 坐标按 B＝B0＋ky(k 为正的常量)的规律变化．两个完全相同的正方形线框甲和乙的上边均与 y 轴垂直，甲的初始位 置高于乙的初始位置，两线框平面均与磁场垂直．现同时分别给甲、乙竖直向下的初速度 v1 和 v2，且 v1＞ v2，若磁场的范围足够大，不计甲、乙间的相互作用，以下说法正确的是 (　　) A．开始时线框中感应电流甲比乙大 B．开始时线框所受磁场的作用力甲比乙小 C．运动中两线框所受磁场的作用力方向相反 D．最终两线框以相同的速度匀速下落 【答案】　AD 9.在一磁感应强度 B=0.5T 的匀强磁场中，垂直于磁场方向水平放置着两根相距 h=0.1m 的平行金属导轨 MN 与 PQ，导轨的电阻忽略不计，在两根导轨的端点 N、Q 之间连接一阻值 R=0.3Ω的电阻.导轨上跨放着一根 长为 L=0.2m、每米长电阻 r=2.0Ω/m 的金属棒 ab.金属与导轨正交放置，交点为 c、d.当金属棒在与导轨平 行的水平外力作用下，以速度 v=4.0m/s 向左做匀速运动时（如图所示），试求： （1）电阻 R 中的电流强度大小和方向； （2）使金属棒做匀速运动的外力； （3）金属棒 ab 两端点间的电势差. 【解析】金属棒向左匀速运动时，等效电路如图所示，在闭合回路中，金属棒的 cd 部分相当于电源，内阻 rcd=hr，电动势 Ecd=Bhv 10.如图甲所示，一端封闭的两条平行光滑导轨相距 L，距左端 L 处的中间一段被弯成半径为 H 的 圆弧， 导轨左右两段处于高度相差 H 的水平面上.圆弧导轨所在区域无磁场，右段区域存在磁场 B0，左段区域存在 均匀分布但随时间线性变化的磁场 B（t），如图乙所示，两磁场方向均竖直向上.在圆弧顶端，放置一质量 为 m 的金属棒 ab，与导轨左段形成闭合回路，从金属棒下滑开始计时，经过时间 t0 滑到圆弧顶端.设金属棒 在回路中的电阻为 R，导轨电阻不计，重力加速度为 g. （1）问金属棒在圆弧内滑动时，回路中感应电流的大小和方向是否发生改变？为什么？ （2）求 0 到时间 t0 内，回路中感应电流产生的热量； （3）探讨在金属棒滑到圆弧底端进入匀强磁场 B0 的一瞬间，回路中感应电流的大小和方向. 【解析】（1）感应电流的大小和方向均不发生改变.因为金属棒滑到圆弧任意位置时，回路中磁通量的变化 率相同. 1 4 （3）设金属进入磁场 B0 一瞬间的速度变 v，金属棒在圆弧区域下滑的过程中，机械能守恒： 在很短的时间内，根据法拉第电磁感应定律，金属棒进入磁场 B0 区域瞬间的感应电动势为 E，则 由闭合电路欧姆定律得： 解得感应电流： 根据上式讨论： Ⅰ.当 时，I=0； Ⅱ.当 ＞ 时， ，方向为 b→a； Ⅲ.当 ＜ 时， 2 2 1 mvmgH = )(,, 2 0 tBLxLBt xvtE ∆+∆=∆Φ∆ ∆=∆ ∆Φ= R EI = )2( 0 0 t LgHR LBI −= 0 2 t LgH = hH2 0t L )2( 0 0 t LgHR LBI −= hH2 0t L ，方向为 a→b. 11.如图所示，空间存在方向竖直向下的磁场，MN、PQ 是水平放置的平行长直导轨，其间距 L＝0.2 m．额 定电压为 2 V 的小灯泡接在导轨一端， ab 是跨接在导轨上内阻不计的导体棒，开始时 ab 与 NQ 的距离为 0.2 m. (1)若导体棒固定不动，要使小灯泡正常发光，磁感应强度随时间的变化率是多大？ (2)若磁感应强度保持 B＝2 T 不变，ab 匀速向左运动，要使小灯泡正常发光，ab 切割磁感线的速度是多大？ 【答案】(1)50 T/s　(2)5 m/s 12.其同学设计一个发电测速装置，工作原理如图所示．一个半径为 R＝0.1 m 的圆形金属导轨固定在竖直平 面上，一根长为 R 的金属棒 OA，A 端与导轨接触良好，O 端固定在圆心处的转轴上．转轴的左端有一个半 径为 r＝ 的圆盘，圆盘和金属棒能随转轴一起转动．圆盘上绕有不可伸长的细线，下端挂着一个质量为 m＝ 0.5 kg 的铝块．在金属导轨区域内存在垂直于导轨平面向右的匀强磁场，磁感应强度 B＝0.5 T．a 点与导轨 相连，b 点通过电刷与 O 端相连．测量 a、b 两点间的电势差 U 可算得铝块速度．铝块由静止释放，下落 h＝ 0.3 m 时，测得 U＝0.15 V．(细线与圆盘间没有滑动，金属棒、导轨、导线及电刷的电阻均不计，重力加速 度 g＝10 m/s2)． (1)测 U 时，a 点相接的是电压表的“正极”还是“负极”？ (2)求此时铝块的速度大小； (3)求此下落过程中铝块机械能的损失． 【答案】(1)正极　(2)2 m/s　(3)0.5 J )2( 0 0 gHt L R LBI −= 13.如图，匀强磁场垂直铜环所在的平面，导体棒 a 的一端固定在铜环的圆心 O 处，另一端紧贴圆环，可绕 O 匀速转动．通过电刷把铜环、环心与两竖直平行金属板 P、Q 连接成如图所示的电路，R 1、R2 是定值电 阻．带正电的小球通过绝缘细线挂在两板间 M 点，被拉起到水平位置；合上开关 K，无初速度释放小球， 小球沿圆弧经过 M 点正下方的 N 点到另一侧． 已知：磁感应强度为 B；a 的角速度大小为 ω，长度为 l，电阻为 r；R1＝R2＝2r，铜环电阻不计；P、Q 两 板间距为 d；带电的小球质量为 m、电量为 q；重力加速度为 g.求： (1)a 匀速转动的方向； (2)P、Q 间电场强度 E 的大小； (3)小球通过 N 点时对细线拉力 FT 的大小． 【答案】见解析 【解析】1)依题意，小球从水平位置释放后，能沿圆弧向下摆动，故小球受到电场力的方向水平向右，P 板 带正电，Q 板带负电．由右手定则可知，导体棒 a 顺时针转动． (2)导体棒 a 转动切割磁感线，由法拉第电磁感应定律得电动势大小： ε＝ ＝ Bl2ω① 由闭合电路欧姆定律：I＝ ② 由欧姆定律可知，PQ 的电压为：UPQ＝IR2③ 故 PQ 间匀强电场的电场强度大小：E＝ ④ 联立①②③④，代入 R1＝R2＝2r，可得：E＝ ⑤ (3)设细线长度为 L，小球到达 N 点时速度为 v，由动能定理可得： mgL－EqL＝ mv2⑥ 又 FT－mg＝ ⑦ 由⑤⑥⑦得：FT＝3mg－ ⑧。学 14.如图所示，在虚线圆周内有一均匀的磁场，其磁感应强度 B 正以 0.1 T/s 的变化率减小．在圆周内放一金 属圆环 (图中实线) ，使圆环平面垂直磁场．已知此圆环半径为 0.1 m. (1)圆环中产生的感应电动势为多大？ (2)设圆环的电阻为 1 Ω，则圆环中的电流为多大？ (3)仍设圆环的电阻为 1 Ω，但在环上某处将圆环断开，并在断开形成的两端点间接入一个 4 Ω 的电阻，这两 端点的电压为多大？ 【答案】(1)3.14×10－3 V　(2)3.14×10－3 A　(3) 2.51×10－3 V 15.如图甲所示，平行导轨 MN、PQ 水平放置，电阻不计，两导轨间距 d＝10 cm，导体棒 ab、cd 放在导轨 上，并与导轨垂直．每根棒在导轨间的部分，电阻均为 R＝1.0 Ω，用长为 L＝20 cm 的绝缘丝线将两棒系 住．整个装置处在匀强磁场中，t＝0 的时刻，磁场方向竖直向下，丝线刚好处于未被拉伸的自然状态．此 后，磁感应强度 B 随时间 t 的变化如图乙所示．不计感应电流磁场的影响，整个过程丝线未被拉断．求：(1)0 2.0 s 的时间内，电路中感应电流的大小与方向；(2)t＝1.0 s 时，丝线的拉力大小． 【答案】(1)1.0×10－3 A　顺时针　(2)1.0×10－5 N