新课标人教版2013届高三物理总复习一轮课时作业10

新课标人教版2013届高三物理总复习一轮课时作业10

新课标人教版2013届高三物理总复习一轮课时作业 课时作业10　牛顿运动定律的综合应用 时间：45分钟　　满分：100分 一、选择题(8×8′＝64′)‎ 图1‎ ‎1．如图1所示，在光滑水平面上叠放着A、B两物体，已知mA＝‎6 kg、mB＝‎2 kg，A、B间动摩擦因数μ＝0.2，在物体A上系一细线，细线所能承受的最大拉力是20 N，现水平向右拉细线，g取‎10 m/s2，则 (　　)‎ A．当拉力F<12 N时，A静止不动 B．当拉力F>12 N时，A相对B滑动 C．当拉力F＝16 N时，B受A的摩擦力等于4 N D．无论拉力F多大，A相对B始终静止 解析：设A、B共同运动时的最大加速度为amax，最大拉力为Fmax 对B：μmAg＝mBamax，amax＝＝6 m/s2‎ 对A、B：Fmax＝(mA＋mB)amax＝48 N 当Fm2，A、B间水平连接着一轻质弹簧秤．若用大小为F的水平力向右拉B，稳定后B的加速度大小为a1，弹簧秤示数为F1；如果改用大小为F的水平力向左拉A，稳定后A的加速度大小为a2，弹簧秤示数为F2.则以下关系式正确的是 (　　)‎ A．a1＝a2，F1>F2　　　　　 B．a1＝a2，F1a2，F1>F2‎ 解析：整体法分析，无论用F拉A，还是拉B，F＝(m1＋m2)a均成立，所以稳定后A的加速度a1和B的加速度a2相等．F拉B时，对A分析，F1＝m1a，F拉A时，对B分析，F2＝m2a，因m1>m2，故F1>F2，所以选项A正确．‎ 答案：A 图3‎ ‎3．如图3所示，当车厢向前加速前进时，物体M静止于竖直车厢壁上，当车厢加速度增加时，则 (　　)‎ ‎①静摩擦力增加　‎ ‎②车厢竖直壁对物体的弹力增加　‎ ‎③物体M仍保持相对于车厢的静止状态 ‎④物体的加速度也增加 A．①②③ B．②③④‎ C．①②④ D．①③④‎ 答案：B 图4‎ ‎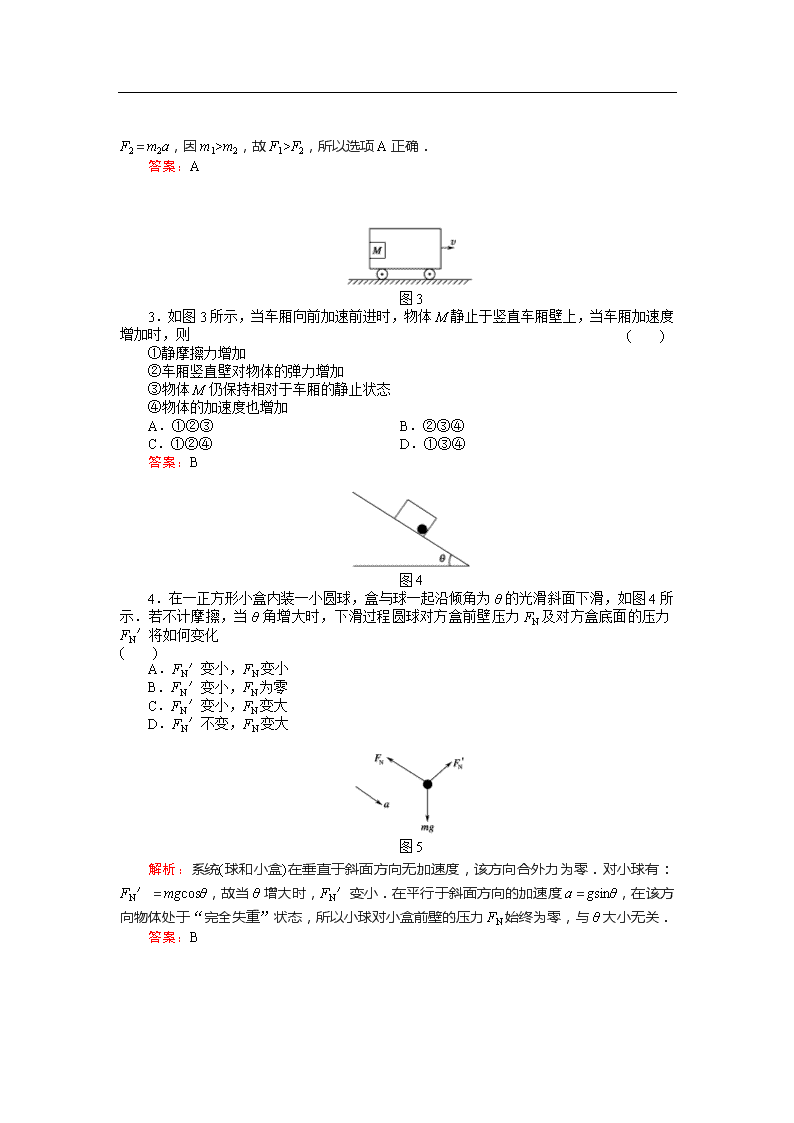4．在一正方形小盒内装一小圆球，盒与球一起沿倾角为θ的光滑斜面下滑，如图4所示．若不计摩擦，当θ角增大时，下滑过程圆球对方盒前壁压力FN及对方盒底面的压力FN′将如何变化 (　　)‎ A．FN′变小，FN变小 B．FN′变小，FN为零 C．FN′变小，FN变大 D．FN′不变，FN变大 图5‎ 解析：系统(球和小盒)在垂直于斜面方向无加速度，该方向合外力为零．对小球有：FN′＝mgcosθ，故当θ增大时，FN′变小．在平行于斜面方向的加速度a＝gsinθ，在该方向物体处于“完全失重”状态，所以小球对小盒前壁的压力FN始终为零，与θ大小无关．‎ 答案：B 图6‎ ‎5．如图6所示，质量为m1和m2的两个物体用细线相连，在大小恒定的拉力F作用下，‎ 先沿水平面，再沿斜面(斜面与水平面成θ角)，最后竖直向上运动．则在这三个阶段的运动中，细线上张力的大小情况是 (　　)‎ A．由大变小 B．由小变大 C．始终不变 D．由大变小再变大 解析：设细线上的张力为F1.要求F1，选受力少的物体m1为研究对象较好；此外还必须知道物体m1的加速度a，要求加速度a，则选m1、m2整体为研究对象较好．‎ 在水平面上运动时：‎ F1－μm‎1g＝m‎1a①‎ F－μ(m1＋m2)g＝(m1＋m2)a②‎ 联立①②解得：F1＝ 在斜面上运动时：‎ F1－m1gsinθ－μm1gcosθ＝m‎1a③‎ F－(m1＋m2)gsinθ－μ(m1＋m2)gcosθ＝(m1＋m2)a④‎ 联立③④解得：F1＝ 图7‎ 同理可得，竖直向上运动时，细线上的张力F1仍是 答案：C ‎6．如图7所示，一轻绳通过一光滑定滑轮，两端各系一质量分别为m1和m2的物体，m1放在地面上，当m2的质量发生变化时，m1的加速度a的大小与m2的关系图象大体如下图中的 (　　)‎ 答案：D 图8‎ ‎7．如图8所示，质量为M的框架放在水平地面上，一轻弹簧上端固定在框架上，下端固定一个质量为m的小球，小球上下振动时，框架始终没有跳起，当框架对地面压力为零瞬间，小球的加速度大小为 (　　)‎ A．g　　　　　　　　 B.g C．0 D.g 解析：弹簧的弹力与框架的重力平衡，故小球受的合外力为(M＋m)g.对m由牛顿第二定律得：(M＋m)g＝ma，所以该瞬间a＝g.‎ 答案：D 图9‎ ‎8．如图9所示，竖直放置在水平面上的轻质弹簧上叠放着两物块A、B，A、B的质量均为‎2 kg，它们处于静止状态．若突然将一个大小为10 N，方向竖直向下的力施加在物块A上，则此瞬间，A对B的压力大小为：(g＝‎10 m/s2) (　　)‎ A．10 N B．20 N C．25 N D．30 N 解析：对AB整体分析，当它们处于静止状态时，弹簧的弹力等于整体AB的重力，当施加力F的瞬间，弹力在瞬间不变，故A、B所受合力为10 N，则a＝F合/(2m)＝2.5 m/s2，后隔离A物块受力分析，得F＋mg－FN＝ma，解得FN＝25 N，所以A对B的压力大小也等于25 N.‎ 答案：C 二、计算题(3×12′＝36′)‎ 图10‎ ‎9．有5个质量均为m的相同木块，并列地放在水平地面上，如图10所示，已知木块与地面间的动摩擦因数为μ，当木块1受到水平力F的作用时，5个木块同时向右做匀加速运动，求：‎ ‎(1)匀加速运动的加速度．‎ ‎(2)第4块木块所受合力．‎ ‎(3)第4块木块受到第3块木块作用力的大小．‎ 解析：(1)选5个木块组成的系统为研究对象，设每一木块受到的滑动摩擦力为Ff，则系统所受外力的合力是：‎ F合＝F－5Ff＝F－5μmg 系统的质量是5m，由牛顿第二定律得：F－5μmg＝5ma 故系统的加速度是a＝＝－μg ‎(2)选第4块木块为研究对象，由牛顿第二定律可直接求得合力F4合＝ma＝－μmg 图11‎ ‎(3)选第4、第5两木块组成的系统为研究的对象，水平受力如图11所示，由牛顿第二定律得：FN34－2Ff＝2ma，故第4块木块受到第3块木块的作用力为：FN34＝2ma＋2Ff＝‎2m(－μg)＋2μmg＝F 答案：(1)－μg　(2)－μmg　(3)F 图12‎ ‎10．如图12所示，火车箱中有一倾角为30°的斜面，当火车以‎10 m/s2的加速度沿水平方向向左运动时，斜面上的物体m还是与车箱相对静止，求物体m所受的摩擦力的大小和方向．‎ 图13‎ 解析：解法1：m受三个力作用：重力mg，弹力FN，静摩擦力的方向难以确定，我们可假定这个力不存在，那么如图13所示，mg与FN在水平方向只能产生大小F＝mgtanθ的合力，此合力只能产生gtan30°＝的加速度．小于题目给定的加速度，合力不足，故斜面对物体的静摩擦力向下．‎ 由牛顿第二定律列方程：‎ FNcos30°－Ffsin30°＝mg①‎ FNsin30°＋Ffcos30°＝ma②‎ 由①②联立得Ff＝5(－1)m N，方向沿斜面向下．‎ 解法2：如图14所示，假定所受的静摩擦力沿斜面向上，用正交分解法有：‎ 图14‎ FNcos30°＋Ffsin30°＝mg①‎ FNsin30°－Ffcos30°＝ma②‎ ‎①②联立得Ff＝5(1－)m N，为负值，说明Ff的方向与假定的方向相反，应是沿斜面向下．‎ 答案：5(－1)m N　方向沿斜面向下 ‎11．如图15所示，倾角为α的光滑斜面体上有一个小球m被平行于斜面的细绳系于斜面上，斜面体放在水平面上．‎ 图15‎ ‎(1)要使小球对斜面无压力，求斜面体运动的加速度范围．并说明其方向．‎ ‎(2)要使小球对细绳无拉力．求斜面体运动的加速度范围，并说明其方向．‎ ‎(3)若已知α＝60°，m＝‎2 kg，当斜面体以a＝‎10 m/s2向右做匀加速运动时，绳对小球拉力多大？(g取‎10 m/s2)‎ 解析：为确定小球对斜面无压力或对细绳无拉力时斜面体的加速度，应先考虑小球对斜面或细绳的弹力刚好为零时的受力情况，再求出相应加速度．取小球、细绳和斜面体这个整体为研究对象，分析整体的受力情况，再确定斜面体的加速度范围．‎ 图16‎ ‎(1)球对斜面刚好无压力时，细绳与斜面平行，小球只受重力mg和细绳拉力FT的作用，如图16所示．正交分解FT，由牛顿第二定律得 解出a0＝g·cotα 所以在斜面向右运动的加速度a≥a0＝g·cotα时，小球对斜面无压力．‎ 图17‎ ‎(2)当球对细绳刚好无拉力时，小球只受重力mg和斜面支持力FN，如图17所示．正交分解FN后，可知FN的竖直分力与重力平衡，FN的水平分力使m向左加速运动．‎ 所以在球对细绳无拉力作用时，若要使球与斜面体以相同的加速度运动，则斜面体必须以a＝a0＝g·tnaα向左加速运动；‎ 图18‎ 如果斜面体向左运动的加速度a>a0，则小球会相对斜面向右上方滑动，但要注意，若球能滑到细绳悬点上方，细绳会对球再次产生拉力作用．‎ ‎(3)由(1)可知，球对斜面恰好无压力时，a0＝g·cot60°＝×‎10 m/s2，而题设条件a＝‎10 m/s2>a0，因此，这时小球对斜面无压力，且球飞离斜面，如图18所示．将细绳拉力FT正交分解得 解出小球所受细绳拉力FT＝mg＝20 N，拉力方向与水平方向夹角θ＝45°.‎ 答案：(1)a≥gcotα　方向向右　(2)a＝gtanα　方向向左　(3)20 N　与水平方向成45°角