2020高中物理第十六章动量守恒定律第4节碰撞课时训练含解析 人教版选修3-5

2020高中物理第十六章动量守恒定律第4节碰撞课时训练含解析 人教版选修3-5

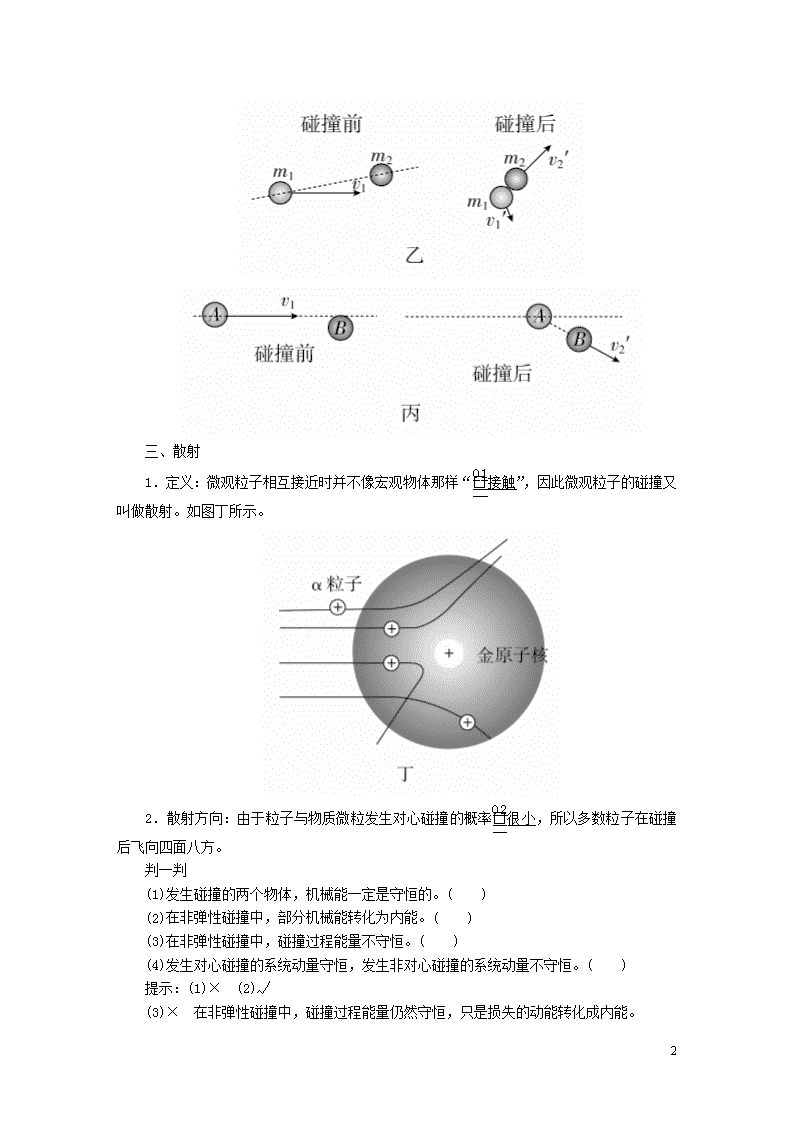
第4节　碰撞 ‎1．掌握弹性碰撞、非弹性碰撞的特点。‎ ‎2．会应用动量、能量的观点综合分析、解决一维碰撞问题。‎ ‎3．了解对心碰撞(正碰)和非对心碰撞的概念。‎ ‎4．知道什么是散射，进一步理解动量守恒定律的普适性。‎ 一、弹性碰撞和非弹性碰撞 ‎1．弹性碰撞：如果碰撞过程中机械能守恒，这样的碰撞叫做弹性碰撞。‎ ‎2．非弹性碰撞：如果碰撞过程中机械能不守恒，这样的碰撞叫做非弹性碰撞。‎ ‎3．一维弹性碰撞分析：假设物体m1以速度v1与原来速度为v2的物体m2发生弹性碰撞，碰撞后它们的速度分别为v1＇、v2＇，碰撞中动量守恒：m1v1＋m2v2＝m1v1′＋m2v2′；碰撞中机械能守恒：m1v＋m2v＝m1v1′2＋m2v2′2。‎ 二、对心碰撞和非对心碰撞 ‎1．正碰(对心碰撞)：一个运动的球与一个静止的球碰撞，碰撞之前球的运动速度与两球心的连线在同一条直线上，碰撞之后两球的速度仍会沿着这条直线。如图甲所示。‎ ‎2．非对心碰撞：一个运动的球与一个静止的球碰撞，如果碰撞之前球的运动速度与两球心的连线不在同一条直线上，碰撞之后两球的速度都会偏离原来两球心的连线。如图乙、丙所示。‎ 12‎ 三、散射 ‎1．定义：微观粒子相互接近时并不像宏观物体那样“接触”，因此微观粒子的碰撞又叫做散射。如图丁所示。‎ ‎2．散射方向：由于粒子与物质微粒发生对心碰撞的概率很小，所以多数粒子在碰撞后飞向四面八方。‎ 判一判 ‎(1)发生碰撞的两个物体，机械能一定是守恒的。(　　)‎ ‎(2)在非弹性碰撞中，部分机械能转化为内能。(　　)‎ ‎(3)在非弹性碰撞中，碰撞过程能量不守恒。(　　)‎ ‎(4)发生对心碰撞的系统动量守恒，发生非对心碰撞的系统动量不守恒。(　　)‎ 提示：(1)×　(2)√‎ ‎(3)×　在非弹性碰撞中，碰撞过程能量仍然守恒，只是损失的动能转化成内能。‎ 12‎ ‎(4)×‎ 想一想 ‎(1)冰壶运动中，两只冰壶相碰撞时，动量守恒吗？‎ 提示：冰壶在光滑的冰面上运动，摩擦力很小，两只冰壶碰撞时的作用力远大于摩擦力，故它们的动量守恒。‎ ‎(2)两球发生正碰，碰后两球的动能之和一定等于碰前两球的动能之和吗？‎ 提示：不一定。发生正碰的两球，在碰撞过程中动能之和可能减少。‎ ‎(3)若两球在光滑水平面上相向运动，碰后均变为静止，则两球碰前的动量具有怎样的关系？‎ 提示：碰撞过程中两球组成的系统动量守恒，依据动量守恒定律可知两球碰前的动量大小相等、方向相反。‎ 课堂任务　弹性碰撞和非弹性碰撞 ‎1．碰撞过程的四个特点 ‎(1)时间短：在碰撞现象中，相互作用的时间很短。‎ ‎(2)相互作用力大：碰撞过程中，相互作用力先急剧增大，后急剧减小，平均作用力很大。‎ ‎(3)位移小：碰撞过程是在一瞬间发生的，时间极短，在物体发生碰撞的瞬间，可忽略物体的位移，认为物体在碰撞前后仍在同一位置。‎ ‎(4)满足动量守恒的条件：系统的内力远远大于外力，所以即使系统所受合外力不为零，外力也可以忽略，系统的总动量守恒。‎ ‎2．弹性碰撞 ‎(1)理解：如果碰撞过程中机械能守恒，这样的碰撞叫做弹性碰撞。‎ ‎(2)发生弹性碰撞时，内力是弹性力，只发生机械能的转移，系统内无机械能损失。‎ 钢球、玻璃球碰撞时的形变能够完全恢复，能量损失很小，它们的碰撞可以看做弹性碰撞；木制品碰撞时形变不能完全恢复，一般情况下不能作为弹性碰撞处理；橡皮泥球之间的碰撞是典型的非弹性碰撞。‎ ‎3．两个物体在同一直线上发生弹性碰撞的分析 ‎(1)若两个物体在水平面上发生弹性碰撞，则这两个物体组成的系统动量守恒，同时总动能也不变。即：‎ m1v1＋m2v2＝m1v1′＋m2v2′‎ m1v＋m2v＝m1v1′2＋m2v2′2‎ 两个质量相等的物体在同一直线上发生弹性碰撞，由方程的对称性可知v1′＝v2，v2′＝v1，则速度互相交换。‎ ‎(2)若碰撞前，有一个物体是静止的，设v2＝0，则碰撞后的速度分别为 v1′＝，v2′＝ ‎①若m1＝m2，v1′＝0，v2′＝v1，碰后实现了动量和动能的全部转移。‎ 12‎ ‎②若m1≫m2，v1′≈v1，v2′≈2v1，碰后m1几乎仍保持原来速度运动，质量小的m2将以2v1向前运动。‎ ‎③若m1≪m2，v1′≈－v1，v2′≈0，碰后m1以原来速率向相反方向运动，m2几乎未动。‎ ‎4．非弹性碰撞 ‎(1)理解：如果碰撞过程中机械能不守恒，这样的碰撞叫做非弹性碰撞。‎ 非弹性碰撞中所产生的形变不能够完全恢复；‎ 非弹性碰撞遵守动量守恒定律，碰撞过程中有机械能损失，能量关系为 m1v＋m2v＞m1v1′2＋m2v2′2。‎ ‎(2)完全非弹性碰撞 两物体碰撞后粘在一起运动，这种碰撞叫做完全非弹性碰撞，碰撞过程遵循动量守恒定律，且动能(或机械能)损失最多。设质量为m1和m2的物体碰前的速度分别为v1和v2，碰后的共同速度为v，则由动量守恒定律有m1v1＋m2v2＝(m1＋m2)v，解得v＝，系统损失的动能ΔEk＝m1v＋m2v－(m1＋m2)v2。‎ ‎5．对碰撞的广义理解 物理学里所研究的碰撞，包括的范围很广，只要通过短时间作用，物体的动量发生了明显的变化，都可视为碰撞。例如：两个小球的撞击、铁锤打击钉子、列车车厢的挂接、子弹射入木块、系在绳子两端的物体将松弛的绳子突然拉直，乃至中子轰击原子核等均可视为碰撞。需注意的是只有将发生碰撞的双方包括在同一个系统中，才能对该系统应用动量守恒定律。‎ ‎6．碰撞的种类及特点 ‎7．同一直线上碰撞问题遵循的三个原则 ‎(1)系统动量守恒，即p1＋p2＝p1′＋p2′。‎ ‎(2)系统动能不增加，即Ek1＋Ek2≥Ek1′＋Ek2′或＋≥＋。‎ ‎(3)速度要合理：若碰前两物体同向，则满足v后>v前 12‎ ‎，且原来在前面的物体碰后速度一定增大，即v前′≥v前。若碰前两物体相向运动，碰后两物体的运动方向不可能都不改变。若碰后两物体同向运动，都应满足v后′≤v前′。‎ 例1　(多选)质量为M的带有光滑圆弧轨道的小车静止置于光滑水平面上，如图所示，一质量也为M的小球以速度v0水平冲上小车，到达某一高度后，小球又返回小车的左端，则(　　)‎ A．小球以后将向左做平抛运动 B．小球将做自由落体运动 C．此过程小球对小车做的功为Mv D．小球在弧形轨道上升的最大高度为 ‎(1)小球与小车在相互作用过程中动量是否守恒？‎ 提示：由于系统所受外力合力不为零，也不能忽略，故系统动量不守恒。由于小球与小车所组成的系统，在水平方向不受外力，所以在水平方向动量守恒。‎ ‎(2)小球与小车在相互作用过程中机械能是否守恒？‎ 提示：由于小球与小车所组成的系统，只发生动能和重力势能的相互转化，没有发生机械能与其他形式的能量之间的相互转化，所以球与小车在相互作用过程中机械能守恒。‎ ‎[规范解答]　小球上升到最高点时与小车相对静止，有相同的速度v′，由动量守恒定律和机械能守恒定律有Mv0＝2Mv′，Mv＝2×＋Mgh，联立解得h＝，D错误；从小球滚上轨道到返回并离开小车，小球和小车组成的系统在水平方向上动量守恒，由于无重力以外的外力做功，系统机械能守恒，此过程类似于弹性碰撞，小车和小球质量相等，作用完成后两者交换速度，即小球速度变为零，之后做自由落体运动，A错误，B、C正确。‎ ‎[完美答案]　BC ‎1.弹性碰撞拓展理解 (1)如果两个相互作用的物体，满足动量守恒的条件，且相互作用过程初、末状态的总机械能不变，广义上也可以看成是弹性碰撞。‎ (2) 12‎ 本题可看成广义上的一动碰一静模型。小球滑上小车轨道时是“碰撞”的开始，小球离开轨道时是“碰撞”的结束。由于系统机械能守恒，所以该过程类似于弹性碰撞，又由于小球和小车质量相等，所以作用完成后小球和小车交换速度。‎ ‎2.多物体、多过程碰撞问题的分析思路 (1)对多个物体组成的系统应用动量守恒定律时，既可以根据作用的先后顺序选取系统，也可以选所有物体为系统，这要由题目需要而定。‎ (2)当问题有多过程、多阶段时，必须分清不同过程的受力特点、力的做功特点等，明确对应过程所遵循的规律。‎ 　质量相等的A、B两球在光滑水平面上沿同一条直线、在同一方向上运动，A球的动量pA＝9 kg·m/s，B球的动量pB＝3 kg·m/s。A球追上B球时发生碰撞，则A、B两球碰撞后的动量可能是(　　)‎ A．pA′＝6 kg·m/s，pB′＝6 kg·m/s B．pA′＝8 kg·m/s，pB′＝4 kg·m/s C．pA′＝－2 kg·m/s，pB′＝14 kg·m/s D．pA′＝－4 kg·m/s，pB′＝17 kg·m/s 答案　A 解析　设A、B两球的质量均为m，以A、B为系统，系统受外力之和为零，A、B组成的系统动量守恒，即pA′＋pB′＝pA＋pB＝9 kg·m/s＋3 kg·m/s＝12 kg·m/s，故先排除了D项。A、B碰撞前的动能之和应大于或等于碰撞后的动能之和，即EkA＋EkB≥EkA′＋EkB′；EkA＋EkB＝＋＝ J＝ J，EkA′＋EkB′＝＋，将A、B、C三项数据代入又可排除C项。A、B两球碰撞后沿同一方向运动，后面A球的速度应小于或等于B球的速度，即vA′≤vB′，代入数据可排除B项，故A正确。‎ 　在光滑的水平面上，质量为m1的小球A以速率v0向右运 动。在小球A的前方O点处有一质量为m2的小球B处于静止状态，如图所示。小球A与小球B发生正碰后小球A、B均向右运动。小球B被位于Q处的墙壁弹回后与小球A在P点相遇，PQ＝1.5PO。假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性碰撞，求两小球质量之比。‎ 答案　2∶1‎ 解析　设两小球碰后小球A的速度大小为v1，小球B的速度大小为v2，小球B与墙壁之间的碰撞为弹性碰撞，则碰后小球B速度大小仍为v2。从两小球碰撞后到它们再次相遇，小球A和B的速度大小保持不变，根据它们通过的路程，可知小球B和小球A在碰撞后的速度大小关系为v2＝4v1‎ 两球碰撞过程为弹性碰撞，有 12‎ m1v0＝m1v1＋m2v2‎ m1v＝m1v＋m2v 联立解得＝。‎ 　如图所示，光滑水平地面上有三个物块A、B和C，它们具有相同的质量，且位于同一条直线上。开始时，三个物块均静止。先让A以一定速度与B碰撞，碰后它们粘在一起，然后又一起与C碰撞并粘在一起。求前后两次碰撞中系统损失的动能之比。‎ 答案　3∶1‎ 解析　设三个物块的质量均为m，A与B碰撞前A的速度为v，碰撞后A、B的速度为v1，A、B与C碰撞后的共同速度为v2。由动量守恒定律得 mv＝2mv1‎ mv＝3mv2‎ 设第一次碰撞中系统的动能损失为ΔE1，第二次碰撞中系统的动能损失为ΔE2，由能量守恒定律得 mv2＝(2m)v＋ΔE1‎ (2m)v＝(3m)v＋ΔE2‎ 联立以上四式解得ΔE1∶ΔE2＝3∶1。‎ A组：合格性水平训练 ‎1. (弹性碰撞)在光滑的水平面上有三个完全相同的小球，它们在同一条直线上，2、3小球静止，并靠在一起，1小球以速度v0射向它们，如图所示。设碰撞中不损失机械能，则碰后三个小球的速度可能值是(　　)‎ A．v1＝v2＝v3＝v0 B．v1＝0，v2＝v3＝v0‎ C．v1＝0，v2＝v3＝v0 D．v1＝v2＝0，v3＝v0‎ 答案　D 解析　两个质量相等的小球发生弹性正碰，碰撞过程中动量守恒，机械能守恒，碰撞后将交换速度，故D正确。‎ 12‎ ‎2．(非弹性碰撞)质量相等的三个物块在一光滑水平面上排成一条直线，且彼此隔开了一定的距离，如图所示。具有动能E0的第1个物块向右运动，依次与其余两个静止物块发生碰撞，最后这三个物块粘在一起，这个整体的动能为 (　　)‎ A．E0 B. C. D. 答案　C 解析　碰撞中动量守恒mv0＝3mv1，得v1＝。E0＝mv，Ek′＝×3mv，联立解得Ek′＝×3m2＝×＝，故C正确。‎ ‎3．(弹性碰撞)在光滑水平面上有两个相同的弹性小球A、B，质量都是m，B球静止，现A球向B球运动，发生正碰，已知碰撞过程中总机械能守恒，两球压缩最紧时的弹性势能为Ep，则碰撞前A的速度等于(　　)‎ A. B. C．2 D．2 答案　C 解析　两球压缩最紧时速度相等，设为v，碰前A球的速度为vA，由动量守恒定律得mvA＝2mv，弹性势能Ep＝mv－×2mv2，联立解得vA＝2，C正确。‎ ‎4．(碰撞的理解与判断)现有甲、乙两滑块，质量分别为3m和m，以相同的速率v在光滑水平面上相向运动，发生了碰撞。已知碰撞后，甲滑块静止不动，那么这次碰撞是(　　)‎ A．弹性碰撞 B．非弹性碰撞 C．完全非弹性碰撞 D．条件不足，无法确定 答案　A 解析　以甲滑块的运动方向为正方向，由动量守恒定律得：3mv－mv＝0＋mv′，所以v′＝2v。碰前总动能为Ek＝×3mv2＋mv2＝2mv2，碰后总动能Ek′＝mv′2＝2mv2，则Ek＝Ek′，所以这次碰撞是弹性碰撞，故A正确。‎ ‎5．(碰撞的判断)(多选)质量为1 kg的小球以4 m/s的速度与质量为2 kg的静止小球发生正碰，关于碰后的速度v1′和v2′，下列选项中可能正确的是(　　)‎ A．v1′＝v2′＝ m/s B．v1′＝－1 m/s，v2′＝2.5 m/s C．v1′＝1 m/s，v2′＝3 m/s D．v1′＝3 m/s，v2′＝0.5 m/s 12‎ 答案　AB 解析　碰撞前两球的总动量为p＝m1v1＝1×4 kg·m/s＝4 kg·m/s，碰撞前总动能为Ek＝m1v＝×1×42 J＝8 J。若v1′＝v2′＝ m/s，则碰撞后总动量为p′＝m1v1′＋m2v2′＝(1＋2)× kg·m/s＝4 kg·m/s，系统动量守恒；碰撞后总动能为Ek′＝(m1＋m2)v1′2＝ J<8 J，总动能没有增加，符合能量守恒定律，A正确。若v1′＝－1 m/s，v2′＝2.5 m/s，碰后总动量为p′＝m1v1′＋m2v2′＝1×(－1) kg·m/s＋2×2.5 kg·m/s＝4 kg·m/s，系统动量守恒；碰撞后总动能为Ek′＝m1v1′2＋m2v2′2＝×1×(－1)2 J＋×2×2.52 J＝6.75 J，系统总动能没有增加，B正确。若v1′＝1 m/s，v2′＝3 m/s，则碰撞后总动量为p′＝m1v1′＋m2v2′＝1×1 kg·m/s＋2×3 kg·m/s＝7 kg·m/s，违背动量守恒定律，C错误。若v1′＝3 m/s，v2′＝0.5 m/s，碰后两球同向运动，后面小球的速度大于前面小球的速度，不符合实际，D错误。‎ ‎6．(非弹性碰撞)冰球运动员甲的质量为80 kg，当他以5 m/s的速度向前运动时，与另一质量为100 kg、速度为3 m/s的迎面而来的运动员乙相撞。碰后甲恰好静止，假设碰撞时间极短，求：‎ ‎(1)碰后乙的速度的大小；‎ ‎(2)碰撞中总机械能的损失。‎ 答案　(1)1 m/s　(2)1400 J 解析　(1)设运动员甲、乙的质量分别为m、M，碰前速度大小分别为v、v1，碰后乙的速度大小为v1′，设碰前运动员甲的速度方向为正方向，‎ 由动量守恒定律有mv－Mv1＝Mv1′‎ 代入数据得v1′＝1 m/s。‎ ‎(2)设碰撞过程中总机械能的损失为ΔE，应有 mv2＋Mv＝Mv1′2＋ΔE 解得ΔE＝1400 J。‎ ‎7．(弹性碰撞)如图所示，ABC为一固定在竖直平面内的光滑轨道，BC段水平，AB段与BC段平滑连接，质量为m1的小球从高为h处由静止开始沿轨道下滑，与静止在轨道BC段上质量为m2的小球发生碰撞，碰撞后两球的运动方向处于同一水平线上，且在碰撞过程中无机械能损失，求碰撞后小球m2的速度大小v2。‎ 答案　 12‎ 解析　设m1碰撞前的速度为v0，根据机械能守恒定律有m1gh＝m1v 设碰撞后m1与m2的速度分别为v1和v2，根据动量守恒定律有m1v0＝m1v1＋m2v2‎ 由于碰撞过程中无机械能损失，有 m1v＝m1v＋m2v 联立解得v2＝。‎ B组：等级性水平训练 ‎8．(非弹性碰撞)(多选)质量分别为m1和m2的两个物体碰撞前后的位移—时间图象如图所示，以下说法中正确的是(　　)‎ A．碰撞前两物体动量相同 B．质量m1等于质量m2‎ C．碰撞后两物体一起做匀速直线运动 D．碰撞前两物体动量大小相等、方向相反 答案　BD 解析　由图线的斜率可知，两物体碰撞前速度大小相等，方向相反，而碰后速度都为零，设两物体碰撞前速度大小分别为v1、v2，系统碰撞前后动量守恒，以v1方向为正方向，则m1v1－m2v2＝0，可得m1v1＝m2v2，则碰前两物体动量大小相等、方向相反，同时可得m1＝m2，故A、C错误，B、D正确。‎ ‎9．(碰撞的判断)(2019·湖南省醴陵二中期中)(多选)在光滑水平面上，一质量为m、速度大小为v的A球与质量为2m静止的B球发生正碰，碰撞可能是弹性的，也可能是非弹性的，则碰后B球的速度大小可能是(　　)‎ A．0.7v B．0.6v C．0.4v D．0.2v 答案　BC 解析　以两球组成的系统为研究对象，以碰前A球的速度方向为正方向，如果碰撞为弹性碰撞，由动量守恒定律得mv＝mvA＋2mvB，由机械能守恒定律得mv2＝mv＋·2mv，联立解得vA＝－v，vB＝v，负号表示碰撞后A球反向弹回；如果碰撞为完全非弹性碰撞，由动量守恒定律得mv＝(m＋2m)vB，解得vB＝v。则碰撞后B球的速度范围是v＜vB＜v，所以碰后B 12‎ 球的速度大小可能是0.6v和0.4v，不可能是0.7v和0.2v，A、D错误，B、C正确。‎ ‎10．(碰撞的判断)如图所示，在光滑水平面上有直径相同的a、b两球，在同一直线上运动，选定向右为正方向，两球的动量分别为pa＝6 kg·m/s、pb＝－4 ‎ kg·m/s。当两球相碰之后，两球的动量可能是(　　)‎ A．pa＝－6 kg·m/s，pb＝4 kg·m/s B．pa＝－6 kg·m/s，pb＝8 kg·m/s C．pa＝－4 kg·m/s，pb＝6 kg·m/s D．pa＝2 kg·m/s，pb＝0‎ 答案　C 解析　对于碰撞问题要遵循三个规律：动量守恒定律、碰后系统的机械能不增加和碰撞过程符合实际情况。本题属于迎面对碰，碰撞前，系统的总动量为2 kg·m/s。A中，系统碰后的动量变为－2 kg·m/s，不满足动量守恒定律，错误；B中，系统碰后的动量变为2 kg·m/s，满足动量守恒定律，但碰后a球动量大小不变，b球动量增加，根据关系式Ek＝可知，a球的动能不变，b球动能增加，系统的机械能增大了，错误；D中，满足动量守恒定律，碰后系统的机械能也没增加，但是碰后a球运动方向不变，b球静止，这显然不符合实际情况，错误；经检验，C满足碰撞所遵循的三个规律，正确。‎ ‎11. (弹性碰撞和非弹性碰撞)如图所示，A、B两物体的质量分别为9m和 ‎10m，A、B间用一轻弹簧连接，质量为m的子弹以水平速度v向右射入A并留在A中。水平面光滑，则当弹簧被压缩到最短时，子弹速度是多大？此时弹性势能是多少？‎ 答案　0.05v　mv2 ‎ 解析　子弹射入A的过程，取向右为正方向，根据动量守恒定律得mv＝(m＋9m)v1‎ 解得v1＝0.1v 弹簧被压缩至最短时，A、B速度相等，根据动量守恒定律得10mv1＝(10m＋10m)v2‎ 解得v2＝0.05v 此时弹性势能是Ep＝·10mv－·20mv 解得Ep＝mv2。‎ 12‎ ‎12．(弹性碰撞)(2019·河北省唐山市期末)如图所示，光滑曲面与粗糙平面平滑连接，质量为m2＝3 kg的滑块B静止在光滑曲面的底端，质量为m1＝2 kg的滑块A由曲面上某一高度为H处无初速度释放，滑到底端和滑块B发生弹性正碰，碰后滑块B在平面上滑行的距离为L＝2 m，已知两滑块与平面间的动摩擦因数均为μ＝0.4，重力加速度g＝10 m/s2。求：‎ ‎(1)滑块B在碰撞后获得的速度大小；‎ ‎(2)滑块A的释放高度H。‎ 答案　(1)4 m/s　(2)1.25 m 解析　(1)碰后滑块B减速滑行，设碰后B的速度为v2，由动能定理－μm2gL＝－m2v ‎ 解得v2＝4 m/s。‎ ‎(2)两滑块发生弹性碰撞，设碰前A的速度为v0，碰后A的速度为v1，‎ 由动量守恒定律和机械能守恒定律得 m1v0＝m1v1＋m2v2 ，m1v＝m1v＋m2v 滑块A下滑过程中，由动能定理得m1gH＝m1v 联立解得H＝1.25 m。‎ 12‎