2020浙江名校高中物理竞赛模拟试题四及答案及评分标准(16页)

2020浙江名校高中物理竞赛模拟试题四及答案及评分标准(16页)

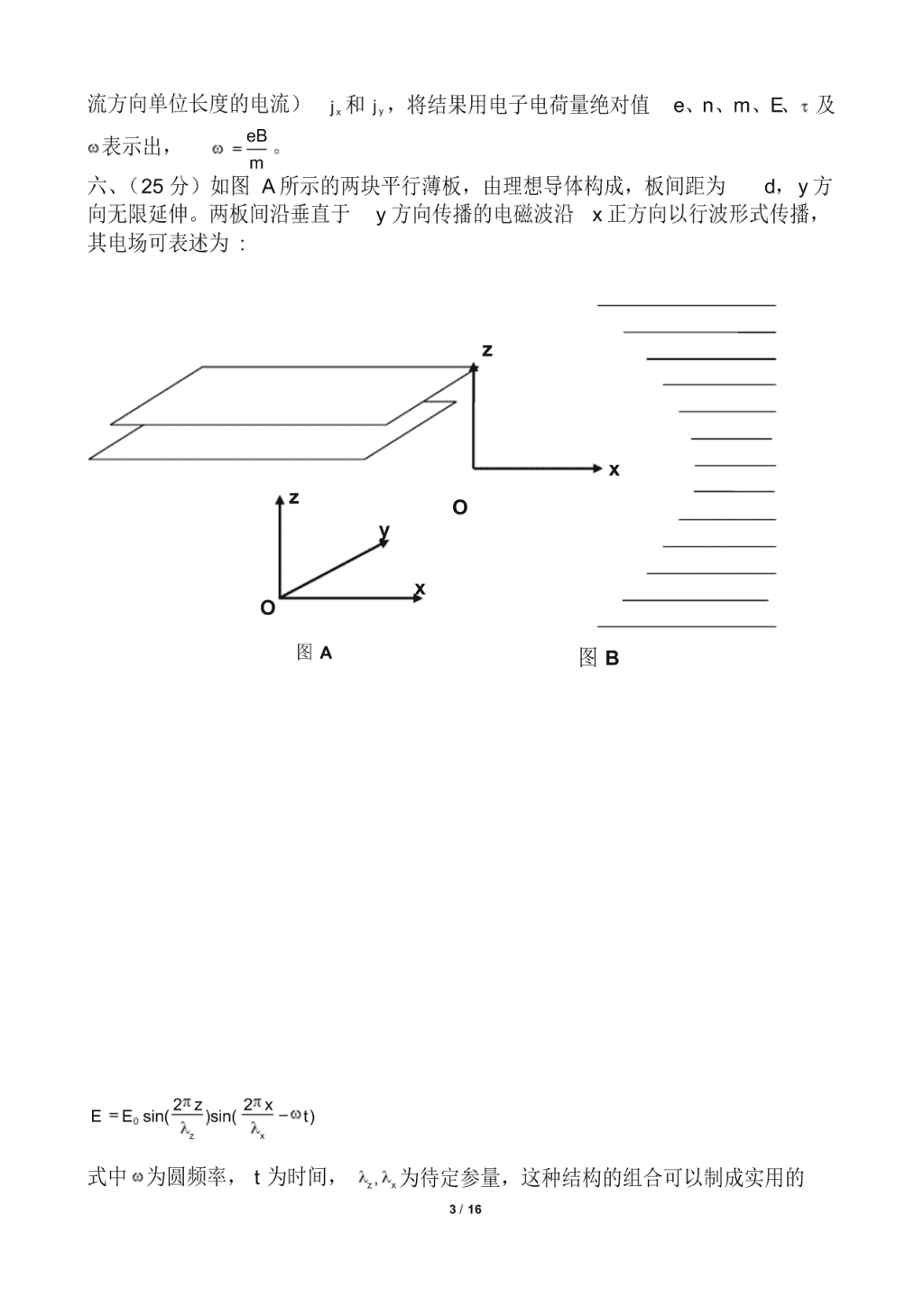
1 / 16 2020 浙江名校高中物理竞赛模拟试题四 一、填空题（每题 5 分，共 20 分） 1. 某光滑曲面由曲线 ( )y f x 绕竖直 y 轴旋转一周形成， 一自然半径为 a、质量为 m 、劲度系数为 k 的弹性圆环置于该曲面之上，能水平静止于任意高度，则曲线 方程为 。 2.如图所示的电阻框架为四维空间中的超立方体在三维空间中的投影模型 （可视 为内外两个立方体框架，对应顶点互相连接起来） ，若该结构中每条棱均由电阻 R的材料构成，则 AB 节点间的等效电阻为 。 3.某种蜜蜂的眼睛能够看到平均波长为 500nm的光， 它是由 5000 个小眼构成的复 眼，小眼一个个密集排放在眼睛的整个表面上，小眼构造很精巧，顶部有一个 透光的圆形集光装置，叫角膜镜；下面连着圆锥形的透明晶体，使得外部入射 的光线汇聚到圆锥顶点连接的感光细胞上（入射进入一个小眼的光线不会透过 锥壁进入其他小眼） ，从而造成一个“影像点” （像素）；所有小眼的影像点就拼 成了一个完整的像。若将复眼看作球面圆锥，球面半径 1.5r mm，则蜜蜂小眼角 膜镜的最佳直径 d 约为（请给出两位有效数字） 。 4.开路电压 0U 与短路电流 SCI 是半导体 p-n 结光电池的两个重要技术指标，试给 出两者之间的关系表达式： 0U = ，式中各符 号代表的物理量分别 为 。 二、（15 分）天体或微观系统的运动可借助计算机动态模拟软件直观显示。这涉 及几何尺寸的按比例缩放。为使显示的运动对缩放后的系统而言是实际可发生 2 / 16 的，运动时间也应缩放。 1.在牛顿力学框架中， 设质点在力场 ( )F r 中作轨道运动， 且有 ( ) ( )kF r F r ，k 为 常数， r 为位矢。若几何尺寸按比率 缩放显示，确定运行时间的缩放率 。 2.由此证明，行星绕太阳轨道运动周期的平方与轨道几何尺寸的立方成正比。 三、 （20 分）在水平面上有两根垂直相交的内壁光滑的连通细管，管内放置两个 质量均为 m、电荷量均为 q 的同号带点质点 A 和 B。初始时，质点 A 至两管交 点 O 的距离为 d，质点 B 位于交点 O 处，速 度相互垂直，方向如图所示，大小均为 2 0 kqu md ，k 为静电力常量。求在以后的运 动中，它们之间的最小距离。 四、 （10 分）热机和热泵利用物质热力学循 环实现相反功能： 前者从高温处吸热， 将部 分热量转化为功对外输出， 其余向低温处放 出；后者依靠外界输入功，从低温处吸热， 连同外界做功转化成的热量一起排向高温 处，按热力学第二定律， 无论热机还是热泵， 若工作物质循环过程中只与温度为 1 2,T T 的 两个热源接触，则吸收的热量 1 2,Q Q 满足不 等式 1 2 1 2 0Q Q T T ，其中热量可正可负，分别表示从热源吸热与向热源放热。 原供暖设备原本以温度 T0 的锅炉释放的热量向房间直接供暖， 使室内温度 保持恒温 T1,高于户外温度 T2。为提高能源利用率，拟在利用原有能源的基础上 采用上述机器改进供暖方案，与直接供暖相比，能耗下降的理论极限可达到多 少？ 五、 （15 分）磁场会影响电子的运动，从而使存在磁场时的电流与电压之间的关 系偏离我们熟悉的欧姆定律，本题研究的问题即为一例。 设 xoy 平面内有密度（单位体积内的电子数）为 n 的二维电子气。平面内沿 x 轴方向存在均匀电场 E Ei （ i 为轴正方向的单位矢量） ，垂直于平面的 z 轴方 向存在匀强磁场， 磁感应强度为 B Bk （ k 为 z 轴正方向的单位矢量） 。已知平面 内的电子运动受到的散射阻力与速度 v 成正比，可等效地用一时间参量 描述为 mv ，m 为电子质量，试求在稳态沿 x 和 y 方向的电流密度（大小为垂直于电 y x A u0 B u0 O d 3 / 16 流方向单位长度的电流） xj 和 yj ，将结果用电子电荷量绝对值 e、n、m、E、 及 表示出， eB m 。 六、（25 分）如图 A 所示的两块平行薄板，由理想导体构成，板间距为 d，y 方 向无限延伸。两板间沿垂直于 y 方向传播的电磁波沿 x 正方向以行波形式传播， 其电场可表述为 : 0 2 2sin( )sin( ) z x z xE E t 式中 为圆频率， t 为时间， ,z x 为待定参量，这种结构的组合可以制成实用的 y x z O 图 A x O z 图 B 4 / 16 微波发射天线，用来代替传统的巨大抛物面天线，可以大幅度降低天线成本。 1.证明 z 只能取如下值： 2 , 1,2,3z d m m ⋯⋯⋯⋯.. 2.当 m=1 时，求 z 。 3.如将一系列板间距相等而长度不等的理想导体相对于沿 y 方向无限延伸的线 状波源（与纸面交与 O 点）平行对称叠排，板的右端对齐，面板的长度有一定 的分布（此结构与与纸面相交的截面图如图 B所示） ，则在这一结构的右端可输 出沿 x 方向传播的平面电磁波。 试给出满足这一要求的板堆在 xoz截面内左侧边 缘（如图 b 所示）所满足的曲线方程。 （取 m=1，已知波源到板堆左端的水平距 离为 L）. 七、（35 分）1.在经典的氢原子模型中，电子围绕原子核做圆周运动，电子的向 心力来自于核电场的作用。可是，经典的电磁理论表明电子做加速运动会发射 电磁波，其发射功率可表示为（拉莫尔公式） ： 2 2 3 06 e aP c ，其中 a 为电子的加 速度，c 为真空光速， 0 1 4 k =8.854 10-12 F m-1,电子电荷量绝对值 e=1.602 10-19C。 若不考虑相对论效应，试估计在经典模型中氢原子的寿命 。（实验测得氢原子 的结合能是 13.6HE eV ，电子的静止质量 31 0 9.109 10m kg ） 2.带点粒子加速后发射的电磁波也有重要的应用价值。 当代科学研究中应用广泛 的同步辐射即是由以接近光速运动的电子在磁场中作曲线运动改变运动方向时 所产生的电磁辐射，电子存储环是同步辐射光源装置的核心，存储环中的电子 束团通过偏转磁铁等装置产生高性能的同步辐射光。上海光源是近年来建成的 第三代同步辐射光源，它的部分工作参数如下：环内电子能量 3.50E GeV ,电子 束团流强 300I mA，周长 L=432m,单元数（装有偏转磁铁的弯道数量） N =20， 5 / 16 偏转磁铁磁场的磁感应强度 B=1.27T。使计算该设备平均每个光口的辐射总功率 P0 。 （在电子接近光速时，若动量不变，牛顿第二定律仍然成立，但拉莫尔公式不 再适用，相应的公式变化为 2 2 4 3 06 e aP c ，其中 2 0 E m c ，E为电子总能量， 2 0m c 为电子的静止能量。 ） 3.由于存储环内的电子的速度接近光速， 所以同步辐射是一个沿电子轨道的切线 方向的光锥，光锥的半顶角为 1 ，由此可见电子的能量越高，方向性越好。 试计算： 上述设备在辐射方向上某点接受到的单个电子产生的辐射持续时间 T 。 （本题结果均请以三位有效数字表示。 ） 物理竞赛模拟四答案 一、 1、 2 22 ( )y C x a mg （C为任意常数） 。 6 / 16 2、 7 12 R 3、 30 m 4、 0 ln 1SC S IkTU e I ，式中 e 为电子电量的绝对值， k 为波尔兹曼常量， T 为绝 对温度， SI 为 p-n 结的反向饱和电流。 评分标准： 本题共 20 分。 第 1、2 题每题填对均得 5 分，第 3 题只要答案在 27-30 m之间即得 5 分，否则 0 分。第 4 题第一空格占 4 分，第二空格占 1 分。 二、 1.设位矢、时间缩放分别为 / /, ,r r t t 故速度、加速度满足关系 / / / /0 0 lim lim t t r rv v t t （1） / / / / 2 200 lim limtt v va v t t (2) 缩放前后质点均满足牛顿运动方程，即 ( )ma F r (3) / /( )ma F r (4) 利用（ 2）式及 ( ) ( )kF r F r ，（4）式化简为 1 2 ( )kma F r （5） 7 / 16 对照（ 3）式，得 1 2 k （6） 2.万有引力场中，有 2k ，设想轨道尺寸按 / l （7） 缩放，则周期按 1 / 2 （8） 缩放，故有 / 2 2 /3 3l l （9） 评分标准： 本题共 15 分 第一小题占 10 分，正确得出（ 6）式得得 10 分，其中正确得出（ 5）式得 5 分。 第二小题占 5 分。正确得出（ 9）式得 5 分。 三、两质点的相对位矢为 A Br r r ，记其单位矢量为 r re r 。由于质点约束在管 内运动，所受合力必定沿运动方向，即静电力沿运动方向的分力，两质点运动 方程 2 2 ( )A r kqma e i i r 2 2 ( )B r kqma e j j r （1） 相减可得 8 / 16 2 2 r kqma e r （2） 其中 B Aa a a 为 B 相对于 A 的加速度。（2）式表明， B 相对于 A 的运动即力心 固定之库仑势场中质点的 m 运动，其电势能为： 2 2 kqU r (3) 中心力场中运动质点的角动量、能量守恒。此处角动量与能量均应为 B 相对 A 的运动的值，可由初始条件定出： 2 0 0( ) kqL mdi u j u i md md （4） 2 2 2 0 0 1 ( ) 2 2 kq kqE m u j u i d d （5） 所求量即近力心点到力心的距离 mr ，该点速度 mu 必与矢径 m rr e 垂直，故有： 2 m m kqmr u md md (6) 2 2 2 2 1 2 2 m m kq kqmru r d (7) 从而解得 1 5 4 r d （8） 评分标准： 本题共 20 分 正确得出（ 3）式得 10 分；（4）、（5）、(6)、(7)与 (8)各占 2 分。 四、 为表述方便，以下热量均用绝对值表示。 9 / 16 可以采用热机热泵联合供暖方案：利用热机从锅炉吸收热量，转化为功；此 功驱动热泵，从户外吸热，向室外放热。 热机的高温热源锅炉，低温热源可选室内或户外环境。以室外为例，设热机 从锅炉吸热 0Q ,向室外放热 10Q ，则有 0 10 0 0 0Q Q T T (1) 热泵的高、低温热源分别为室内、 户外环境。 设热泵从户外吸热 2 ,Q 向室外放热 12 ,Q 则有 (2) 通过热机、热泵联合工作，室内获得的总能量为 1 10 12Q Q Q (3) 将（ 1）、（2）两式相加，得 0 2 1 0 2 1 0Q Q Q T T T (4) 若热机以户外环境为低温热源，同理可得上式。 由能量守恒定律给出 1 0 2Q Q Q （5） 直接供暖时，给室内供热 1,Q 锅炉所释放的热量为 / 0 1Q Q （6） 联立（ 4）（5）两式，可得热机热泵供暖锅炉释放的热量为 12 2 1 2 0Q Q T T 10 / 16 0 1 2 0 1 1 0 2 ( ) ( ) T T TQ Q T T T （7） 能耗下降率为 / 0 0 2 0 1 / 0 1 0 2 ( ) ( ) Q Q T T T Q T T T （8） 理论极限为上式取等号。 评分标准： 本题共 10 分，其中（ 4）式占 4 分。 六、 1．已知两板间的电磁波的电场强度 E为 0 2 2sin( )sin( ) z x z xE E t （1） 由于是理想导体板，当 z=0和 d 时应有 E=0。从而 22 , , 1,2,3......z z dd m m m （2） 2.对于（ 1）式描述的电磁波，可以通过 1sin sin [cos( ) cos( )] 2 （3） 表达为两列平面电磁波的叠加， 1 2E E E 1 0 1 2 2cos( ) 2 x z x zE E t （4） 2 0 1 2 2cos( ) 2 x z x zE E t 式中两列电磁波的波长 0 都可表达为 11 / 16 2 2 2 2 0 1 1 1 2x z c （5） 当 m=1, 2 ,z d 2 1 1( )2 2 z c d (6) 3．因此 ,x 方向的波速 xv 为 2 ( )2 1 x x cv c d (7) 如图所示，设板堆左端任一点 P 到波源的距离 OP=R，OP与水平线的交角为 。 要使得输出为沿水平方向的平面波，应满足， cos x R L RL c c v （8） 由此可得， 2 2 (1 1 )(1 1 cos )c cR L d d （9） 评分标准：本题共 25 分 第一小题 5 分，第二小题 10 分，第三小题 10 分； x O z R P 12 / 16 其中（ 2）式占 5 分，（5）式占 6 分，(6)式占 4 分；（8）式占 6 分。 七、 由方程 F ma （1） 2va r （2） 2 2 0 1 4 eF r （3） 可推导出电子的总能量为 2 0 08 eU r （4） 由条件 13.6HE eV 推导出氢原子的轨道半径和运动速度分别为： 11 0 5.29 10r m （5） 6 0 2.19 10 /v m s （6） 由拉莫尔公式得初始发射功率 2 2 3 06 e aP c 6 3 3 3 2 4 0 096 e c m r （7） 在微小的时间间隔 t 中，辐射使电子的总能量 U 减少 U P t （8） 2 2 2 0 0 1 1( ) 8 8 e eU r r r r r （9） 其中 r 为电子轨道半径的减少量，由此可导出时间和半径 r 的变化方程： 2 3 2 2 2 20 0 4 12 4 ,c m rt r A r r e （10） 其中 3 2 2 0 4 3 c mA e 。 构造一个半径为 r0 的球体， 则 24 r r 即为距离球心为 r 的薄球壳的体积， 在 13 / 16 0r 到 0 的求和过程中可以算出球的体积为 3 0 4 3 r 。对应本题情况解出电子轨道从 0r 减少到 0 所需的时间为 2 3 2 2 3 0 0 4 4 c m rt e （11） 代入数据，得： 111.56 10 s （12） 2： 对于高能电子有 v c (1) 2E mc (2) 2va r (3) F eBc (4) F ma (5) 以上条件可以得出电子的偏转半径： ER ecB (6) 储存环中的电子数量： Q I tn e e 14 / 16 (7) 其中 t 为电子旋转一圈所花费的时间。由（ 3）式及辐射条件可得每个电子每圈 损失的总能量为（电子在直道上不辐射能量） ： 2 2 4 2 4 3 0 0 2 6 3neu e a R eE c c R （8） 由（ 7）（8）得到存储环中的电子消耗的总功率为： 4 5 0 4.34 10 3 neu utal nE IeP W t R (9) 出光口的功率为： 4 0 2.17 10utalPP W N (10) 3: 在电子轨道上某点的切线方向上的某一点 P处观察，观察者只能在一个很短时 间间隔内看到电子发出的辐射，这段时间是电子地速度方向改变圆锥顶角（即 2 ）的角度所对应的光到达接受位置的时间间隔。在这段时间内电子移动的距 离为 2Rx (1) 令 v c ，则电子在这两点发出的辐射时间间隔为： 2 1 2Rt t c (2) 15 / 16 但在轨道的切线方向上观察，上述时间还要扣除 A 点发射出的光到达 B点位置 所花费的时间 2Rt c ， (3) 则 2 1T t t t (4) 又 2 2 2 0 1 1 mc m c (5) 由 1 0 可得 2 2 1(1 ) (6) 代入（ 4）式得到 3 RT c (7) 代入数据得： 209.51 10T s (8) 评分标准： 本题共 35 分 第 1 小题 10 分，其中（ 4）（5）式各占 1 分。 第 2 小题 12 分，其中（ 6）式与（ 7）式各占 1 分，（8）式占 6 分。 R t 2 B A x t1 2/ 16 / 16 第 3 小题 13 分，其中（ 4）式占 5 分。