- 2021-05-28 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【物理】河南省新安县第一高级中学2019-2020学年高一5月月考试题
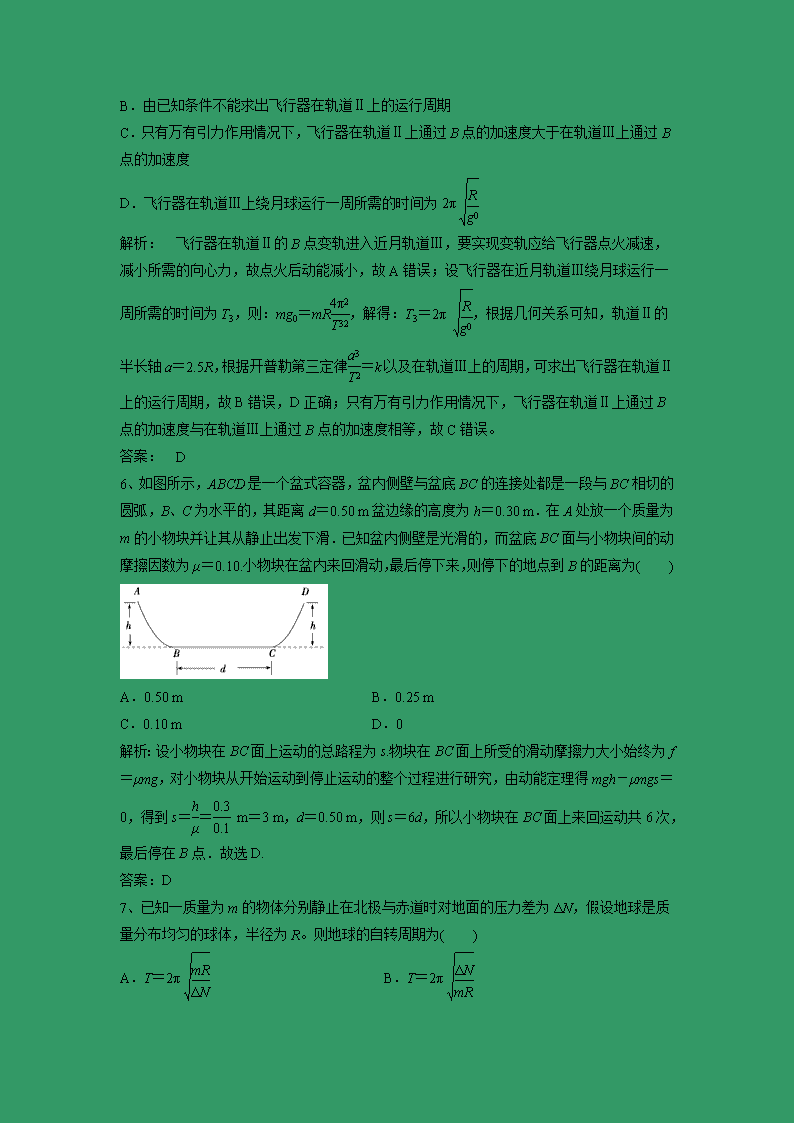
河南省新安县第一高级中学2019-2020学年5月月考试题 一、选择题(共15小题,每小题3分,共45分,其中是1-9是单选题,10-15是多选题) 1、关于摩擦力做功,以下说法正确的是( ) A.滑动摩擦力阻碍物体的相对运动,所以一定做负功 B.静摩擦力虽然阻碍物体间的相对运动趋势,但不做功 C.静摩擦力和滑动摩擦力不一定都做负功 D.一对相互作用力,若作用力做正功,则反作用力一定做负功 解析:摩擦力可以是动力,故摩擦力可做正功;一对相互作用力,可以都做正功,也可以都做负功;静摩擦力可以做功,也可以不做功,故选项A、B、D错误,C正确. 答案:C 2、假设地球是一半径为R、质量分布均匀的球体。一矿井深度为d,已知质量分布均匀的球壳对壳内物体的引力为零。矿井底部和地面处的重力加速度大小之比为( ) A.1- B.1+ C.2 D.2 解析: 如图所示, 根据题意,地面与矿井底部之间的环形部分对处于矿井底部物体的引力为零。设地面处的重力加速度为g,地球质量为M,地球表面的物体m受到的重力近似等于万有引力,故mg=G;设矿井底部处的重力加速度为g′,等效“地球”的质量为M′,其半径r=R-d,则矿井底部处的物体m受到的重力mg′=G,又M=ρV=ρ·πR3,M′=ρV′=ρ·π(R-d)3,联立解得=1-,A对。 答案: A 3、以相同的动能从同一点水平抛出两个物体a和b,落地点的水平位移为s1和s2,自抛出到落地的过程中,重力做的功分别为W1、W2,落地瞬间重力的即时功率为P1和P2( ) A.若s1<s2,则W1>W2,P1>P2 B.若s1<s2,则W1>W2,P1<P2 C.若s1=s2,则W1>W2,P1>P2 D.若s1=s2,则W1<W2,P1<P2 解析:若s1<s2,由于高度决定了平抛运动的时间,所以两个物体运动时间相等. 由x=v0t知:水平抛出两个物体的初速度关系为v1<v2. 由于以相同的动能从同一点水平抛出,所以两个物体的质量关系是m2<m1. 自抛出到落地的过程中,重力做的功W=mgh,所以W1>W2,平抛运动竖直方向做自由落体运动,所以落地瞬间两个物体的竖直方向速度vy相等,根据瞬时功率P=Fvcos α,落地瞬间重力的即时功率P=mgvy. 由于m2<m1,所以P1>P2,故A正确,B错误. 以相同的动能从同一点水平抛出两个物体a和b,由于高度决定时间,所以两个物体运动时间相等. 若s1=s2,平抛运动水平方向做匀速直线运动,所以水平抛出两个物体的初速度相等.由于以相同的动能从同一点水平抛出,所以两个物体的质量相等.所以自抛出到落地的过程中,重力做的功相等,即W1=W2.落地瞬间重力的即时功率相等,即P1=P2,则C、D错误.故选A. 答案:A 4、近年来,人类发射的多枚火星探测器已经相继在火星上着陆,正在进行着振奋人心的科学探究,为我们将来登上火星、开发和利用火星资源奠定了基础。如果火星探测器环绕火星做“近地”匀速圆周运动,并测得该运动的周期为T,则火星的平均密度ρ的表达式为(k为某个常数)( ) A.ρ=kT B.ρ= C.ρ=kT2 D.ρ= 解析:选D 火星探测器环绕火星做“近地”匀速圆周运动时,=mR,又M=πR3·ρ,可得ρ==,故D正确。 5、如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞行器在距月球表面高度为3R的圆形轨道Ⅰ上运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动,则( ) A.飞行器在B点处点火后,动能增加 B.由已知条件不能求出飞行器在轨道Ⅱ上的运行周期 C.只有万有引力作用情况下,飞行器在轨道Ⅱ上通过B点的加速度大于在轨道Ⅲ上通过B点的加速度 D.飞行器在轨道Ⅲ上绕月球运行一周所需的时间为2π 解析: 飞行器在轨道Ⅱ的B点变轨进入近月轨道Ⅲ,要实现变轨应给飞行器点火减速,减小所需的向心力,故点火后动能减小,故A错误;设飞行器在近月轨道Ⅲ绕月球运行一周所需的时间为T3,则:mg0=mR,解得:T3=2π ,根据几何关系可知,轨道Ⅱ的半长轴a=2.5R,根据开普勒第三定律=k以及在轨道Ⅲ上的周期,可求出飞行器在轨道Ⅱ上的运行周期,故B错误,D正确;只有万有引力作用情况下,飞行器在轨道Ⅱ上通过B点的加速度与在轨道Ⅲ上通过B点的加速度相等,故C错误。 答案: D 6、如图所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,B、C为水平的,其距离d=0.50 m盆边缘的高度为h=0.30 m.在A处放一个质量为m的小物块并让其从静止出发下滑.已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数为μ=0.10.小物块在盆内来回滑动,最后停下来,则停下的地点到B的距离为( ) A.0.50 m B.0.25 m C.0.10 m D.0 解析:设小物块在BC面上运动的总路程为s.物块在BC面上所受的滑动摩擦力大小始终为f=μmg,对小物块从开始运动到停止运动的整个过程进行研究,由动能定理得mgh-μmgs=0,得到s== m=3 m,d=0.50 m,则s=6d,所以小物块在BC面上来回运动共6次,最后停在B点.故选D. 答案:D 7、已知一质量为m的物体分别静止在北极与赤道时对地面的压力差为ΔN,假设地球是质量分布均匀的球体,半径为R。则地球的自转周期为( ) A.T=2π B.T=2π C.T=2π D.T=2π 解析:选A 在北极,物体所受的万有引力与支持力大小相等,在赤道处,物体所受的万有引力与支持力的差值提供其随地球自转的向心力,由题意可得ΔN =mR2,解得T=2π ,A正确。 8、质量为2×103 kg、发动机的额定功率为80 kW的汽车在平直公路上行驶.若该汽车所受阻力大小恒为4×103 N,则下列判断中正确的有( ) A.汽车的最大速度是10 m/s B.汽车以2 m/s2的加速度匀加速启动,启动后第2 s末时发动机的实际功率是32 kW C.汽车以2 m/s2的加速度匀加速启动,匀加速运动所能维持的时间为10 s D.若汽车保持额定功率启动,则当其速度为5 m/s时,加速度为8 m/s2 解析:当牵引力大小等于阻力时速度最大,根据P=fvm得,汽车的最大速度vm== m/s=20 m/s,故A错误;根据牛顿第二定律,得F-f=ma,解得F=f+ma=4 000 N+2 000×2 N=8 000 N,第2 s末的速度v=at=2×2 m/s=4 m/s,第2 s末发动机的实际功率P=Fv=8 000×4 W=32 kW,故B正确;匀加速直线运动的末速度v== m/s=10 m/s,做匀加速直线运动的时间t== s=5 s,故C错误;当汽车速度为5 m/s时,牵引力F== N=16 000 N,根据牛顿第二定律,得汽车的加速度a== m/s2=6 m/s2,故D错误.选B. 答案:B 9、嫦娥工程分为三期,简称“绕、落、回”三步走。我国发射的“嫦娥三号”卫星是嫦娥工程第二阶段的登月探测器,经变轨成功落月。若该卫星在某次变轨前,在距月球表面高度为h的轨道上绕月球做匀速圆周运动,其运行的周期为T。若以R表示月球的半径,忽略月球自转及地球对卫星的影响,则( ) A.“嫦娥三号”绕月球做匀速圆周运动时的线速度大小为 B.物体在月球表面自由下落的加速度大小为 C.在月球上发射卫星的最小发射速度为 D.月球的平均密度为 解析:选B “嫦娥三号”绕月球做匀速圆周运动,轨道半径r=R+h,则线速度大小v=,A错误;由=m(R+h),=mg月 ,可得物体在月球表面自由下落的加速度大小g月=,B正确;因月球上卫星的最小发射速度为月球表面卫星的最大环绕速度,有=,又=m(R+h),可得v= ,C错误;由=m(R+h),ρ=,V=πR3,可得月球的平均密度ρ=,D错误。 10、一物体自t=0时开始做直线运动,其速度图线如图所示.下列选项正确的是( ) A.在0~6 s内,物体离出发点最远为30 m B.在0~6 s内,物体经过的路程为40 m C.在0~4 s内,物体的平均速率为7.5 m/s D.在5~6 s内,物体所受的合力做负功 解析:0~5 s内物体向正方向运动,5~6 s内向负方向运动,故5 s末离出发点最远,由面积法求出0~5 s内的位移l1=35 m,A错误;5~6 s内的位移l2=-5 m,总路程为40 m,B正确;由面积法求出0~4 s内的位移l=30 m,此段时间内路程等于位移的大小,故平均速率==7.5 m/s,C正确;由题图象知5~6 s内物体加速运动,合力和位移同向,合力做正功,D错误. 答案:BC 11、2017年,人类第一次直接探测到来自双中子星合并的引力波.根据科学家们复原的过程,在两颗中子星合并前约100 s时,它们相距约400 km,绕二者连线上的某点每秒转动12圈.将两颗中子星都看作是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星( ) A.质量之积 B.质量之和 C.速率之和 D.各自的自转角速度 解析:选BC.由题意可知,合并前两中子星绕连线上某点每秒转动12圈,则两中子星的周期相等,且均为T= s,两中子星的角速度均为ω=,两中子星构成了双星模型,假设两中子星的质量分别为m1、m2,轨道半径分别为r1、r2,速率分别为v1、v2,则有:G=m1ω2r1、G=m2ω2r2,又r1+r2=L=400 km,解得m1+m2=,A错误,B正确;又由v1=ωr1、v2=ωr2,则v1+v2=ω(r1+r2)=ωL ,C正确;由题中的条件不能求解两中子星自转的角速度,D错误. 12、将一物体从地面以一定的初速度竖直上抛,从抛出到落回原地的过程中,空气阻力恒定.以地面为零势能面,则下列反映物体的机械能E、动能Ek、重力势能Ep及克服阻力所做的功W随距地面高度h变化的四个图象中,可能正确的是( ) 解析:物体运动过程中受重力和阻力,除重力外其余力做的功等于机械能的变化量,上升过程和下降过程中物体一直克服阻力做功,故机械能不断减小,但落回原地时有速度,机械能不可能为零,故A错误;物体运动过程中受重力和阻力,合力做功等于动能的变化量,上升过程动能不断减小,表达式为-(mg+f)h=Ek-Ek0,下降过程动能不断增大,表达式为(mg-f)(H-h)=Ek,故B正确;重力做功等于重力势能的减少量,以地面为零势能面,故Ep=mgh,故C正确;上升过程中克服阻力所做的功W=fh,下降过程中克服阻力做的功为W=f(H-h)=fH-fh,故D正确. 答案:BCD 13、某行星的一颗同步卫星绕行星中心做圆周运动的周期为T,假设该同步卫星下方行星表面站立一个观察者,在观察该同步卫星的过程中,发现有T时间看不到该卫星.已知当太阳光照射到该卫星表面时才可能被观察者观察到,该行星的半径为R.则下列说法中正确的是( ) A.该同步卫星的轨道半径为6.6R B.该同步卫星的轨道半径为2R C.行星表面上两点与该同步卫星连线的夹角最大值为60° D.行星表面上两点与该同步卫星连线的夹角最大值为120° 解析:选BC.根据光的直线传播规律,在观察该同步卫星的过程中,发现有T时间看不到该卫星,同步卫星相对行星中心转动角度为θ,则有sin =,结合θ=ωt=×=,解得该同步卫星的轨道半径为r=2R,故B正确,A错误;行星表面上两点与该同步卫星连线的夹角最大值为α,则有rsin =R,所以行星表面上两点与该同步卫星连线的夹角最大值为60°,故C正确,D错误;故选BC. 14、由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内.一质量为m的小球,从距离水平地面高为H的管口D处静止释放,最后能够从A端水平抛出落到地面上.下列说法正确的是( ) A.小球落到地面时相对于A点的水平位移值为2 B.小球落到地面时相对于A点的水平位移值为2 C.小球能从细管A端水平抛出的条件是H>2R D.小球能从细管A端水平抛出的最小高度Hmin=R 【解析】 要使小球从A点水平抛出,则小球到达A点时的速度v>0,根据机械能守恒定律,有mgH-mg·2R=mv2,所以H>2R,故选项C正确,选项D错误;小球从A点水平抛出时的速度v=,小球离开A点后做平抛运动,则有2R=gt2,水平位移x=vt,联立以上各式可得水平位移x=2,选项A错误,选项B正确. 【答案】 BC 15、如图所示,A是地球的同步卫星,B是位于赤道平面内的近地卫星,C为地面赤道上的物体,已知地球半径为R,同步卫星离地面的高度为h,则( ) A.A、B加速度的大小之比为2 B.A、C加速度的大小之比为1+ C.A、B、C线速度的大小关系为vA>vB>vC D.要将B转移到A的轨道上运行至少需要对B进行两次加速 解析:选BD 根据万有引力提供向心力可知G=ma,得aA=G,aB=G,故=2,选项A错误;由题意可知,A、C角速度相同,根据a=ω2r得aA=ω2(R+h),aC=ω2R,故=1+,选项B正确;根据G=m得v= ,可知轨道半径越大线速度越小,所以v B>vA,又A、C角速度相同,根据v=ωr可知vA>vC,故vB>vA>vC,选项C错误;要将B转移到A的轨道上,先要对B加速使其转移到椭圆轨道上,再在椭圆轨道对B加速使其转移到A的轨道上,选项D正确。 二、实验题(每空2分,共12分) 16、在一次验证机械能守恒定律实验中,质量m=1kg 的重物自由下落,在纸带上打出一系列的点,如图1所示(打点间隔为0.02s),单位cm.那么 (1)打点计时器打下计数点B时,物体的速度vB= ; (2)从起点O到打下计数点B的过程中重力势能减少量是△Ep= .此过程中物体动能的增加量△Ek= (g取9.8m/s2); (3)通过计算,数值上△Ep △Ek(填“>”、“=”或“<”),这是因为 ; (4)以各点到起始点的距离h为横坐标,以各点速度的平方v2为纵坐标建立直角坐标系,用实验测得的数据绘出v2﹣h图象,如图2所示:由v2﹣h图线求得重物下落的加速度g′= m/s2.(结果保留三位有效数字) 答案:(1)0.98 m/s; (2)0.49 J;0.48 J (3)>;重物和纸带下落时受到阻力作用 (4)9.71 三、计算题(4小题,共43分) 17、(10分)人造地球卫星P绕地球球心做匀速圆周运动,已知P卫星的质量为m,距地球球心的距离为r,地球的质量为M,引力常量为G,求: (1)卫星P与地球间的万有引力的大小; (2)卫星P的运行周期; (3)现有另一地球卫星Q,Q绕地球运行的周期是卫星P绕地球运行周期的8倍,且P、Q的运行轨迹位于同一平面内,如图所示,求卫星P、Q在绕地球运行过程中,两卫星间相距最近时的距离. 解析:(1)卫星P与地球间的万有引力F=G. (2)由万有引力定律及牛顿第二定律,有G=mr, 解得T=2π . (3)对P、Q两卫星,由开普勒第三定律,可得 =,又TQ=8T, 因此rQ=4r. P、Q两卫星和地球共线且P、Q位于地球同侧时距离最近,故最近距离为d=3r. 答案:(1)G (2)2π (3)3r 18、(10分)我国将于2022年举办冬奥会,跳台滑雪是其中最具观赏性的项目之一.如图所示,质量m=60 kg的运动员从长直助滑道AB的A处由静止开始以加速度a=3.6 m/s2匀加速滑下,到达助滑道末端B时速度vB=24 m/s,A与B的竖直高度差H=48 m.为了改变运动员的运动方向,在助滑道与起跳台之间用一段弯曲滑道衔接,其中最低点C处附近是一段以O为圆心的圆弧.助滑道末端B与滑道最低点C的高度差h=5 m,运动员在B、C间运动时阻力做功W=-1 530 J,取g=10 m/s2. (1)求运动员在AB段下滑时受到阻力Ff的大小; (2)若运动员能够承受的最大压力为其所受重力的6倍,则C点所在圆弧的半径R至少应为多大. 解析:(1)运动员在AB上做初速度为零的匀加速运动,设AB的长度为x,则有v=2ax,① 由牛顿第二定律,有mg-Ff=ma,② 联立①②式,代入数据,解得Ff=144 N.③ (2)设运动员到达C点时的速度为vC,在由B到达C的过程中,由动能定理,有mgh+W=mv-mv,④ 设运动员在C点所受的支持力为FN,由牛顿第二定律,有 FN-mg=m,⑤ 由运动员能够承受的最大压力为其所受重力的6倍,联立④⑤式,代入数据解得R=12.5 m. 答案:(1)144 N (2)12.5 m 19、(11分)如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点,沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡另一点Q上,斜坡的倾角α,已知该星球的半径为R,引力常量为G,已知球的体积公式是V=πR3.求: (1)该星球表面的重力加速度g; (2)该星球的密度; (3)该星球的第一宇宙速度. 解析:(1)小球在斜坡上做平抛运动时: 水平方向上:x=v0t,① 竖直方向上:y=gt2,② 由几何知识tan α=,③ 由①②③式得g=. (2)对于星球表面的物体m0,有G=m0g. 又V=πR3.故ρ==. (3)该星球的第一宇宙速度等于它的近地卫星的运动速度,故G=m, 又GM=gR2, 解得v=. 20、(12分)如图所示,一轻质弹簧左端固定在足够长的水平轨道左侧,水平轨道的PQ段粗糙,调节其初始长度为l0=1.5 m,水平轨道右侧连接半径为R=0.4 m的竖直圆形光滑轨道,可视为质点的滑块将弹簧压缩至A点后由静止释放,经过水平轨道PQ后,恰好能通过圆形轨道的最高点B.已知滑块质量m=1 kg,与PQ段间的动摩擦因数μ=0.4,轨道其他部分摩擦不计.g取10 m/s2,求: (1)弹簧压缩至A点时弹簧的弹性势能Ep; (2)若每次均从A点由静止释放滑块,同时调节PQ段的长度,为使滑块在进入圆形轨道后能够不脱离轨道而运动,PQ段的长度l应满足什么条件? 解析:(1)设滑块冲上圆形轨道最高点B时速度为v,由能量守恒定律,得 Ep=mv2+2mgR+μmgl0,① 滑块在B点时,重力提供向心力,由牛顿第二定律,得 mg=m,② 联立①②式并代入数据,解得Ep=16 J. (2)若要使滑块不脱离轨道,分两种情况讨论: ①滑块能够通过B点而不脱离轨道,则应满足l≤1.5 m,③ ②滑块能够到达圆形轨道,则应满足Ep≥μmgl,解得l≤4 m,④ 滑块到达圆形轨道而又不超过与圆心等高的C点时,如图所示,临界条件取到达C点时速度恰好为零,则有Ep≤mgR+μmgl,解得l≥3 m,⑤ 联立③④⑤式,可得PQ段长度l应满足的条件是: l≤1.5 m或3 m≤l≤4 m. 答案:(1)16 J (2)l≤1.5 m或3 m≤l≤4 m查看更多