解密05+万有引力与航天-备战2019年高考物理之高频考点解密
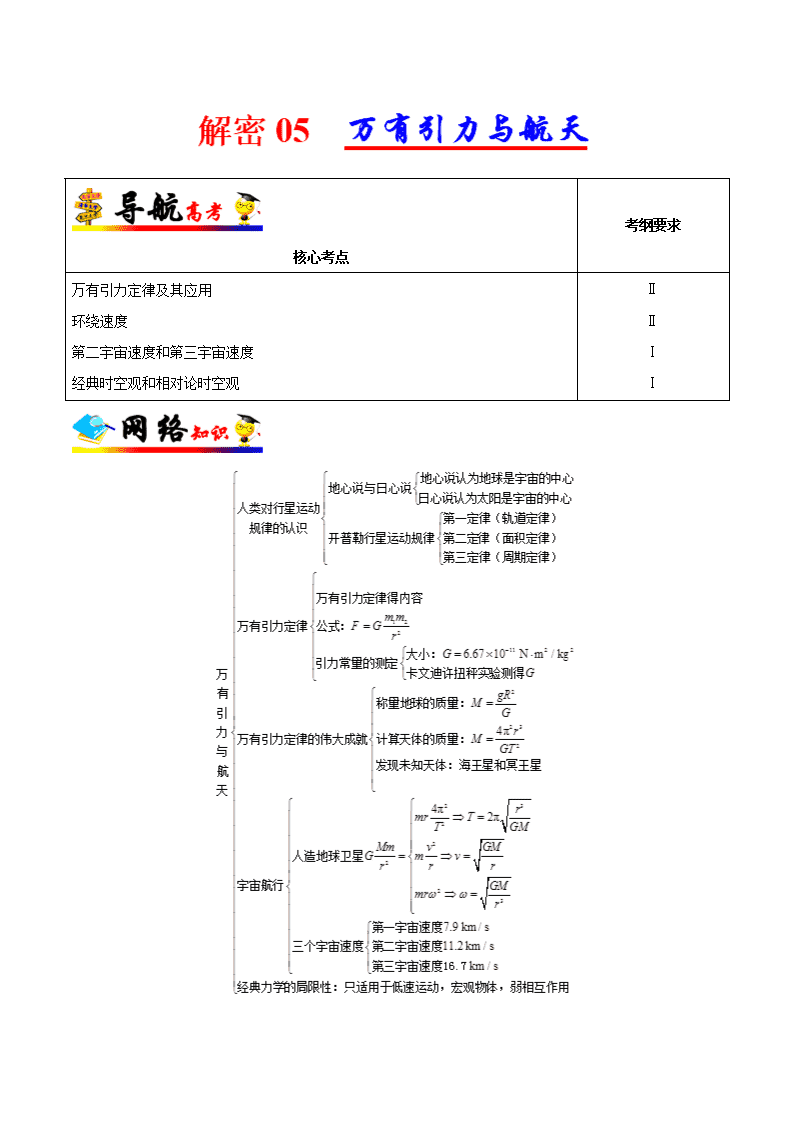
核心考点
考纲要求
万有引力定律及其应用
环绕速度
第二宇宙速度和第三宇宙速度
经典时空观和相对论时空观
Ⅱ
Ⅱ
Ⅰ
Ⅰ
考点1 万有引力与重力
1.在地球表面上的物体
地球在不停地自转、地球上的物体随地球自转而做圆周运动,自转圆周运动需要一个向心力,是重力不直接等于万有引力而近似等于万有引力的原因,如图所示,万有引力为F,重力为G,向心力为Fn。当然,真实情况不会有这么大偏差。
(1)物体在一般位置时Fn=mrω2,Fn、F、G不在一条直线上。
(2)当物体在赤道上时,Fn达到最大值Fnmax,Fnmax=mRω2,重力达到最小值:
,重力加速度达到最小值,。
(3)当物体在两极时Fn=0,G=F,重力达到最大值,重力加速度达到最大值,。
可见只有在两极时重力才等于万有引力,重力加速度达到最大值;其他位置时重力要略小于万有引力,在赤道处的重力加速度最小,两极处的重力加速度比赤道处大;但是由于自转的角速度很小,需要的向心力很小。计算题中,如果未提及地球的自转,一般认为重力近似等于万有引力。即或者写成GM=gR2,称为“黄金代换”。
2.离开地球表面的物体
卫星在做圆周运动时,只受到地球的万有引力作用,我们认为卫星所受到的引力就是卫星在该处所受到的重力,,该处的重力加速度。这个值也是卫星绕地球做圆周运动的向心加速度的值;卫星及内部物体处于完全失重状态。(为什么?)
(2018·山西省祁县中学)万有引力定律能够很好地将天体运行规律与地球上物体运动规律具有的内在一致性统一起来。用弹簧秤称量一个相对于地球静止的小物体的重量,随称量位置的变化可能会有不同的结果。已知地球质量为M,万有引力常量为G。将地球视为半径为R质量均匀分布的球体。下列选项中说法正确的是
A.在赤道地面称量时,弹簧秤读数为
B.在北极地面称量时,弹簧秤读数为
C.在北极上空高出地面h处称量时,弹簧秤读数为
D.在赤道上空高出地面h处称量时,弹簧秤读数为
【参考答案】BC
【试题解析】在赤道地面称量时,万有引力等于重力加上随地球一起自转所需要的向心力,则有
1.(2018·湖南省醴陵市第四中学)英国《每日邮报》网站2015年4月3日发表了题为《NASA有能力在2033年将宇航员送入火星轨道并在2039年首次登陆火星》的报道。已知火星半径是地球半径的,质量是地球质量的,自转周期基本相同。地球表面重力加速度是g,若宇航员在地面上能向上跳起的最大高度是h,在忽略自转影响的条件下,下述分析正确的是
A.火星表面的重力加速度是
B.火星的第一宇宙速度是地球第一宇宙速度的倍
C.宇航员在火星上向上跳起的最大高度是
D.宇航员在火星表面所受火星引力是他在地球表面所受地球引力的倍
【答案】CD
2.如图所示,O为地球的球心,A为地球表面上的点,B为O、A连线间的点,AB=d,将地球视为质量分布均匀的球体,半径为R。设想挖掉以B为圆心、以为半径的球。若忽略地球的自转,则挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为
A. B. C. D.
【答案】B
【解析】本题采用割补法解题,设想没有挖掉以B为圆心、以为半径的球,则A
点物体所受到的引力是以B为圆心、以为半径的球的引力和剩余部分的引力的矢量和,设地球的质量为M,以B为圆心、以为半径的球的质量为,则,,根据万有引力定律有,,,所以,根据牛顿第二定律得:挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为:,所以选B。
3.地球赤道上的重力加速度为g=9.8 m/s2,物体在赤道上的向心加速度约为an=3.39 cm/s2,若使赤道上的物体处于完全失重状态,则地球的转速应为原来的
A.17倍 B.49倍 C.98倍 D.289倍
【答案】A
考点2 人造卫星及宇宙航行
一、卫星的动力学规律
由万有引力提供向心力,。
二、卫星的各物理量随轨道半径变化的规律
1.线速度v:由得,可见,r越大,v越小;r越小,v越大。
2.角速度ω:由得,可见,r越大,ω越小;r越小,ω越大。
3.周期T:由得,可见,r越大,T越大;r越小,T越小。
4.向心加速度an:由得,可见,r越大,an越小;r越小,an越大。
以上结论可总结为“一定四定,越远越慢”。
三、卫星运行参量的比较与运算
卫星名称
离地面距离
运转周期
运转速率
近地卫星
0
84分钟(最小周期)
7.9 km/s(最大环绕速度)
神舟号飞船
350 km
90分钟
7.7 km/s
通讯同步卫星
36 000 km(约6R)
24小时
3.1 km/s
月球
3.8×105 km
27天
1.02 km/s
四、三种宇宙速度
宇宙速度
数值(km/s)
意义
第一宇宙速度
7.9
卫星的最小发射速度,若7.9 km/s≤v<11.2,物体绕地球运行
第二宇宙速度
11.2
物体挣脱地球引力束缚的最小发射速度。若11.2 km/s≤v<16.7 km/s物体绕太阳运行
第三宇宙速度
16.7
物体挣脱太阳引力束缚的最小发射速度,若v≥16.7 km/s,物体将脱离太阳系在宇宙空间运行
注意:
(1)第一宇宙速度的推导有两种方法:①由得 ;②由得。
(2)第一宇宙速度的公式不仅适用于地球,也适用于其他星球,只是M、R0、g必须与之相对应,不能套用地球的参数。
五、卫星变轨问题
人造地球卫星发射过程要经过多次变轨,如图所示,我们从以下几个方面讨论:
1.变轨原理及过程
(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上。
(2)卫星在A点点火加速,由于速度变大,万有引力不足以提供卫星在轨道Ⅰ上做圆周运动的向心力,卫星做离心运动进入椭圆轨道Ⅱ。
(3)在B点(远地点)再次点火加速进入圆轨道Ⅲ。
2.一些物理量的定性分析
(1)速度:设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v1、v3,在轨道Ⅱ上过A点和B点时速率分别为vA、vB。在A点加速,则vA>vB,在B点加速,v3>vB,又因v1>v3,故有vA>v1>v3>vB。
(2)加速度:因为在A点,卫星只受到万有引力作用,故不论从轨道Ⅰ还是轨道Ⅱ上经过A点,卫星的加速度都相同,同理,经过B点加速度也相同。
(3)周期:设卫星在Ⅰ、Ⅱ、Ⅲ轨道上运行周期分别为T1、T2、T3,轨道半径分别为r1、r2(半长轴)、r3,由开普勒第三定律可知T1
a1;对空间站和地球的同步卫星而言,因同步卫星周期小于空间站的周期则,同步卫星的轨道半径较小,根据可知a3>a2,故选项D正确。
3.在星球表面发射探测器,当发射速度为v时,探测器可绕星球表面做匀速圆周运动;当发射速度达到v时,可摆脱星球引力束缚脱离该星球,已知地球、火星两星球的质量比约为10:1,半径比约为2:1,下列说法正确的有
A.探测器的质量越大,脱离星球所需的发射速度越大
B.探测器在地球表面受到的引力比在火星表面的大
C.探测器分别脱离两星球所需要的发射速度相等
D.探测器脱离星球的过程中势能逐渐变大
【答案】BD
能逐渐变大,故选项D正确。
考点3 特殊卫星及天体分析
一、极地卫星和近地卫星
1.极地卫星运行时每圈都经过南北两极,由于地球自转,极地卫星可以实现全球覆盖。
2.近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫星,其运行的轨道半径可近似认为等于地球的半径,其运行的线速度约为7.9 km/s。
二、同步卫星
同步卫星是指相对地球“静止不动”的卫星。
同步卫星的六个“一定”:
轨道平面一定
轨道平面与赤道平面重合
高度一定
距离地心的距离一定,h=4.225×104 km;距离地面的高度为3.6×104 km
环绕速度一定
v=3.08 km/s,环绕方向与地球自转方向相同
角速度一定
周期一定
与地球自转周期相同,常取T=24 h
向心加速度一定
a=0.23 m/s2
三、赤道上的物体与同步卫星以及近地卫星的运动规律
1.地球赤道上的物体,静止在地面上与地球相对静止,随地球的自转绕地轴做匀速圆周运动。地球赤道上的物体受到的地球的万有引力,其中的一个分力提供物体随地球自转做圆周运动的向心力,产生向心加速度a,另一个分力为重力,有G-mg=ma(其中R为地球半径)。
2.近地卫星的轨道高度约等于地球的半径,其所受万有引力完全提供卫星做圆周运动的向心力,即G=ma。
3.同步卫星与赤道上的物体具有与地球自转相同的运转周期和运转角速度,始终与地球保持相对静止状态,共同绕地轴做匀速圆周运动。
4.区别:
(1)同步卫星与地球赤道上的物体的周期都等于地球自转的周期,而不等于近地卫星的周期。
(2近地卫星与地球赤道上的物体的运动半径都等于地球的半径,而不等于同步卫星运动的半径。
(3)三者的线速度各不相同。
四、求解此类试题的关键
1.在求解“同步卫星”与“赤道上的物体”的向心加速度的比例关系时应依据二者角速度相同的特点,运用公式a=ω2r而不能运用公式a=。
2.在求解“同步卫星”与“赤道上的物体”的线速度的比例关系时,仍要依据二者角速度相同的特点,运用公式v=ωr而不能运用公式v=。
3.在求解“同步卫星”运行速度与第一宇宙速度的比例关系时,因都是由万有引力提供的向心力,故要运用公式v=,而不能运用公式v=ωr或v=。
五、双星及多星系统
1.在天体运动中,将两颗彼此相距较近,且在相互之间万有引力作用下绕两者连线上的某点做周期相同的匀速圆周运动的行星称为双星。
2.双星系统的条件:
(1)两颗星彼此相距较近;
(2)两颗星靠相互之间的万有引力做匀速圆周运动;
(3)两颗星绕同一圆心做圆周运动。
3.双星系统的特点:
(1)两星的角速度、周期相等;
(2)两星的向心力大小相等;
(3)两星的轨道半径之和等于两星之间的距离,即r1+r2=L,轨道半径与行星的质量成反比。
4.双星问题的处理方法:
双星间的万有引力提供了它们做圆周运动的向心力,即,由此得出:
(1)m1r1=m2r2,即某恒星的运动半径与其质量成反比;
(2)由于ω=,r1+r2=L,所以两恒星的质量之和。
(2018·安徽省宣城市)如图所示,在火星与木星轨道之间有一小行星带。假设该带中的小行星只受到太阳的引力,并绕太阳做匀速圆周运动。下列说法正确的是
A.太阳对小行星带中各小行星的引力相同
B.同一小行星可在一年内与地球两次相距最近
C.小行星带内侧小行星的向心加速度值大于小行星带外侧小行星的向心加速度值
D.小行星带内各小行星圆周运动的线速度值大于地球公转的线速度值
【参考答案】C
【试题解析】因为小行星的质量不一定相同,则太阳对各小行星的引力不一定相同,故A错误;根据
1.(2018·广东省潮州市)我国“北斗”卫星导航定位系统将由5颗静止轨道卫星(同步卫星)和30颗非静止轨道卫星组成,30颗非静止轨道卫星中有27颗是中轨道卫星,中轨道卫星轨道高度约为2.15×104
km,静止轨道卫星的高度约为3.60×104 km,下列说法正确的是
A.静止轨道卫星的运行周期大于中轨道卫星的运行周期
B.中轨道卫星的线速度大于7.9 km/s
C.静止轨道卫星的线速度大于中轨道卫星的线速度
D.静止轨道卫星的向心加速度大于中轨道卫星的向心加速度
【答案】A
【解析】据万有引力提供向心力有:,据,因为静止轨道卫星轨道半径大于中轨道卫星轨道半径,故A正确;据得,由于中轨道卫星的半径大于地球半径,故中轨道卫星的线速度小于7.9 km/s,故B错误;据得,静止轨道卫星的线速度小于中轨道卫星的线速度,故C错误;据,可知静止轨道卫星的向心加速度小于中轨道卫星的向心加速度,故D错误。
2.双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动。研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化。若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原来的k倍,两星之间的距离变为原来的n倍,则此时圆周运动的周期为
A. B.
C. D.
【答案】B
1.(2018·北京卷)若想检验“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律,在已知月地距离约为地球半径60倍的情况下,需要验证
A.地球吸引月球的力约为地球吸引苹果的力的1/602
B.月球公转的加速度约为苹果落向地面加速度的1/602
C.自由落体在月球表面的加速度约为地球表面的1/6
D.苹果在月球表面受到的引力约为在地球表面的1/60
【答案】B
【解析】设月球质量为,地球质量为M,苹果质量为,则月球受到的万有引力为:,苹果受到的万有引力为:,由于月球质量和苹果质量之间的关系未知,故二者之间万有引力
2.(2018·天津卷)2018年2月2日,我国成功将电磁监测试验卫星“张衡一号”发射升空,标志我国成为世界上少数拥有在轨运行高精度地球物理场探测卫星的国家之一。通过观测可以得到卫星绕地球运动的周期,并已知地球的半径和地球表面的重力加速度。若将卫星绕地球的运动看作是匀速圆周运动,且不考虑地球自转的影响,根据以上数据可以计算出卫星的
A.密度 B.向心力的大小 C.离地高度 D.线速度的大小
【答案】CD
【解析】根据题意,已知卫星运动的周期T,地球的半径R,地球表面的重力加速度g,卫星受到的外有引力充当向心力,故有,卫星的质量被抵消,则不能计算卫星的密度,更不能计算卫星的向心力大小,AB错误;由解得,而,故可计算卫星距离地球表面的高度,C正确;根据公式,轨道半径可以求出,周期已知,故可以计算出卫星绕地球运动的线速度,D正确。
3.(2016·北京卷)如图所示,一颗人造卫星原来在椭圆轨道1绕地球E运行,在P点变轨后进入轨道2做匀速圆周运动。下列说法正确的是
A.不论在轨道1还是轨道2运行,卫星在P点的速度都相同
B.不论在轨道1还是轨道2运行,卫星在P点的加速度都相同
C.卫星在轨道1的任何位置都具有相同加速度
D.卫星在轨道2的任何位置都具有相同动量
【答案】B
4.(2016·四川卷)国务院批复,自2016年起将4月24日设立为“中国航天日”。1970年4月24日我国首次成功发射的人造卫星东方红一号,目前仍然在椭圆轨道上运行,其轨道近地点高度约为440 km,远地点高度约为2 060 km;1984年4月8日成功发射的东方红二号卫星运行在赤道上空35 786 km的地球同步轨道上。设东方红一号在远地点的加速度为a1,东方红二号的加速度为a2,固定在地球赤道上的物体随地球自转的加速度为a3,则a1、a2、a3的大小关系为
A.a2>a1>a3 B.a3>a2>a1
C.a3>a1>a2 D.a1>a2>a3
【答案】D
【解析】东方红二号和固定在地球赤道上的物体转动的角速度相同,根据a=ω2r可知,a2>a3;根据可知a1>a2;故选D。
5.(2016·天津卷)我国即将发射“天宫二号”空间实验室,之后发生“神舟十一号”飞船与“天宫二号”对接。假设“天宫二号”与“神舟十一号”都围绕地球做匀速圆周运动,为了实现飞船与空间实验室的对接,下列措施可行的是
A.使飞船与空间实验室在同一轨道上运行,然后飞船加速追上空间实验室实现对接
B.使飞船与空间实验室在同一轨道上运行,然后空间实验室减速等待飞船实现对接
C.飞船先在比空间实验室半径小的轨道上加速,加速后飞船逐渐靠近空间实验室,两者速度接近时实现对接
D.飞船先在比空间实验室半径小的轨道上减速,减速后飞船逐渐靠近空间实验室,两者速度接近时实现对接
【答案】C
6.(2016·全国新课标Ⅰ卷)利用三颗位置适当的地球同步卫星,可使地球赤道上任意两点之间保持无线电通讯,目前,地球同步卫星的轨道半径为地球半径的6.6倍,假设地球的自转周期变小,若仍仅用三颗同步卫星来实现上述目的,则地球自转周期的最小值约为
A.1 h B.4 h
C.8 h D.16 h
【答案】B
【解析】设地球的半径为R,周期T=24 h,地球自转周期的最小值时,三颗同步卫星的位置如图所示,所以此时同步卫星的半径r1=2R,由开普勒第三定律得,可得,故ACD错误,B正确。
7.(2016·海南卷)通过观测冥王星的卫星,可以推算出冥王星的质量。假设卫星绕冥王星做匀速圆周运动,除了引力常量外,至少还需要两个物理量才能计算出冥王星的质量。这两个物理量可以是
A.卫星的速度和角速度
B.卫星的质量和轨道半径
C.卫星的质量和角速度
D.卫星的运行周期和轨道半径
【答案】AD
8.(2016·上海卷)两颗卫星绕地球运行的周期之比为27:1,则它们的角速度之比为__________,轨道半径之比为___________。
【答案】1:27 9:1
【解析】根据题意,卫星绕地球做匀速圆周运动,卫星的运行角速度与周期关系为:,即角速度与周期成反比,则;两颗卫星做匀速圆周运动,由万有引力提供向心力,则有:,即,所以有:。