2020届高三物理第二轮专题讲座3-4 模块整合 新人教版

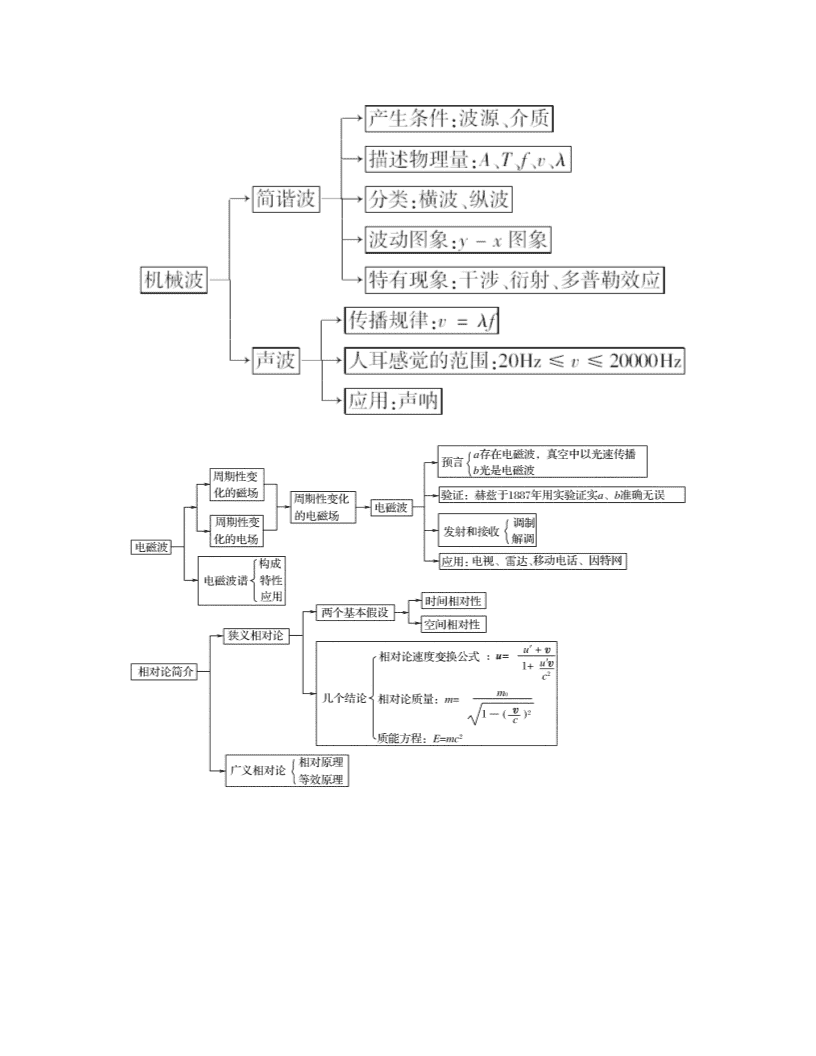
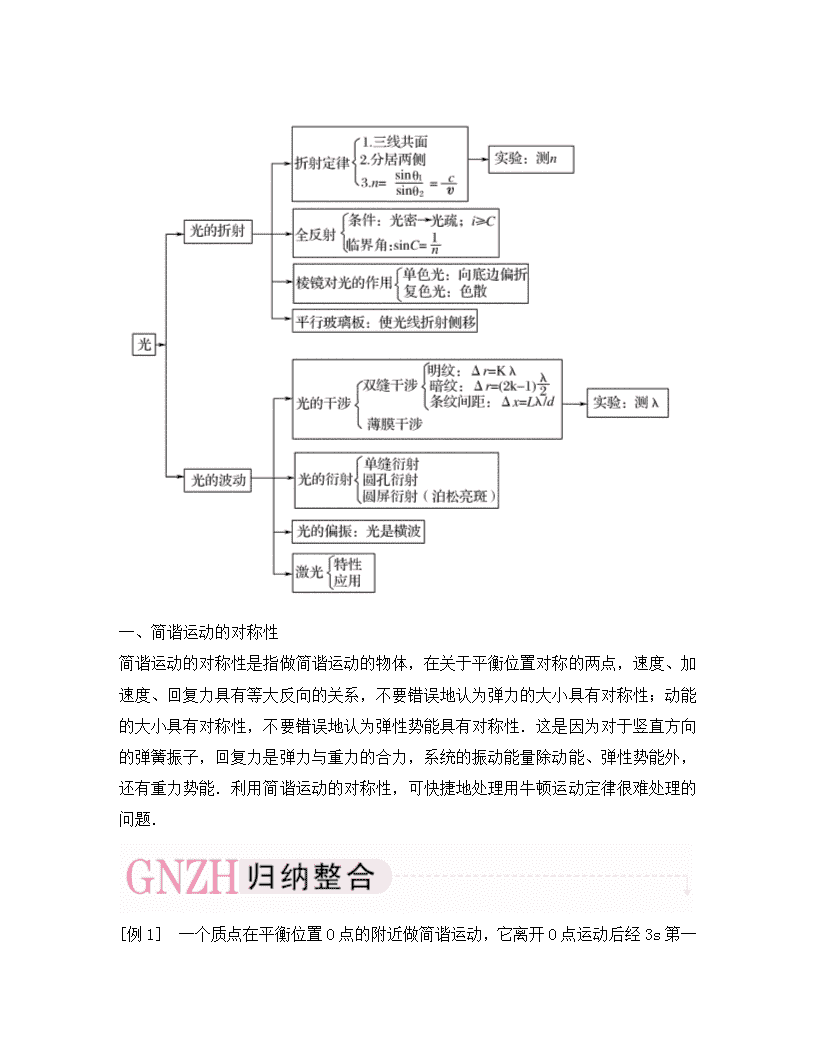
2020届高三物理第二轮专题讲座3-4 模块整合 新人教版

模 块 整 合 ‎ 一、简谐运动的对称性 简谐运动的对称性是指做简谐运动的物体，在关于平衡位置对称的两点，速度、加速度、回复力具有等大反向的关系，不要错误地认为弹力的大小具有对称性；动能的大小具有对称性，不要错误地认为弹性势能具有对称性．这是因为对于竖直方向的弹簧振子，回复力是弹力与重力的合力，系统的振动能量除动能、弹性势能外，还有重力势能．利用简谐运动的对称性，可快捷地处理用牛顿运动定律很难处理的问题．‎ ‎[例1]　一个质点在平衡位置O点的附近做简谐运动，它离开O点运动后经3s 第一次经过M点，再经过2s第二次经过M点，则质点再经过________s第三次经过M点．若该质点由O点出发，在20s内经过的路程是20cm，则质点做振动的振幅为________cm.‎ ‎[解析]　作出该质点做振动的图像如图甲所示，从图乙振动模拟图可看出，M点的位置可能是两个，即如图甲所示的M1或M2.‎ 若是位置M1，由图甲可知 ＝4s，T1＝16s，质点第三次经过M1时，所需时间为Δt1＝16s－2s＝14s，质点在20s内的路程为20cm，故由5A1＝20cm，得振幅A1＝4cm.‎ 若是位置M2，由图可知 ＝4s，T2＝ s，质点第三次经过M2时，所需时间为Δt2＝ s－2s＝ s，质点在20s内的路程为20cm，故由15A2＝20cm，得振幅A2＝ cm.‎ ‎[答案]　14　4或　‎ ‎[总结评述]　在求解过程中，往往容易漏掉了后一解，这是思考问题的不严密．可见用振动图像进行分析，不会出现漏解情况，而且使问题变得直观、简洁．‎ 二、波的图象及其多解性 波形在空间分布的周期性及振动在时间上的周期性是波动问题有多解的两大因素，另外波的传播方向未定，也会带来波动问题的多解．‎ ‎1．传播方向的双向性带来的多解 在二维空间坐标系中，波的传播方向只有两种可能：沿x轴的正方向或负方向．在波的传播方向未定的情况下必须要考虑这一点．‎ ‎2．图形的多样性带来的多解 在波的传播中，质点的振动情况、波的传播方向及波形三者紧密相关．若质点在一定的限制条件(时间、空间、振动状态)下振动，则质点间的波形可能不是唯一的，因此相应的波的参变量可能不是唯一的．‎ ‎3．波传播时间的周期性带来的多解 波在传播过程中，经过整数倍周期时，其波形图线相同．‎ ‎4．解决波动中多解问题的一般思路 ‎(1)首先分析出造成多解的原因．‎ ‎(2)抓住质点周期性运动及其与波的传播之间的联系，并要灵活地用周期个数来表示波的传播时间，用波长个数来表示波的传播距离．‎ ‎(3)然后由λ＝vT进行计算，若有限定条件，再进行讨论．‎ ‎[例2]　一列简谐横波在x轴上传播，在t1＝0和t2＝0.5s两时刻的波形分别如图中的实线和虚线所示，求：‎ ‎(1)若周期大于t2－t1，波速多大？‎ ‎(2)若周期小于t2－t1，则波速又是多少？‎ ‎(3)若波速为92m/s，求波的传播方向．‎ ‎[解析]　(1)若波向右传播，Δx1＝2m，Δt＝t2－t1＝0.5s，则v1＝ ＝4m/s；‎ 若波向左传播，Δx2＝6m，Δt＝t2－t1＝0.5s，则v2＝ ＝12m/s.‎ ‎(2)若波向右传播，Δx3＝(2＋8n)m(n＝1,2,3，…)，Δt＝t2－t1＝0.5s，则v3＝ ＝(4＋16n)m/s(n＝1,2,3，…)；‎ 若波向左传播，Δx4＝(6＋8n)m＝n(1,2,3，…)，Δt＝t2－t1＝0.5s，则v4＝ ＝(12＋16n)m/s(n＝1,2,3，…)．‎ ‎(3)当波速为92m/s时，波向前传播的距离为Δx＝vt＝46m＝ 由图可知波向左传播．‎ ‎[答案]　(1)若波向右传播，波速为4m/s；若波向左传播，波速为12m/s ‎(2)若波向右传播，波速为(4＋16n)m/s(n＝1,2,3，…)‎ 若波向左传播，波速为(12＋16n)m/s(n＝1,2,3，…)‎ ‎(3)向左传播 三、振动图象和波的图象的综合 ‎1．振动图象与波动图象的互换 ‎(1)由振动图象定出振幅、周期及某时刻该质点的振动方向，结合波的传播方向从而可定出某时刻介质中各个质点在该时刻的位置，便可作出该时刻的波动图象．‎ ‎(2)由波动图象定振动图象．从波动图象定出振幅、该时刻某质点的位置及振动方向，再结合波的传播方向定出各个时刻该质点的位置，便可求出该质点的振动图象．‎ ‎2．解决两种图象结合的问题的基本思路 ‎(1)首先识别哪一个是波动图象，哪一个是振动图象，两者间的联系纽带是周期与振幅．‎ ‎(2)再从振动图象中找出某一质点在波动图象中的那一时刻的振动方向，然后再确定波的传播方向及其他问题．‎ ‎[例3]　下图(甲)为一列简谐横波在某一时刻的波形图，图(乙)为质点P以此时刻为计时起点的振动图象．从该时刻起 (　　)‎ A．经过0.35s，质点Q距平衡位置的距离小于质点P距平衡位置的距离 B．经过0.25s，质点Q的加速度小于质点P的加速度 C．经过0.15s，波沿x轴的正方向传播了3m D．经过0.1s，质点Q的运动方向沿y轴正方向 ‎[解析]　t＝0时刻从(乙)图可知(甲)图中P点振动方向沿y辆负向，所以(甲)图中波沿x轴正向传播，(甲)图中各个质点的振动周期相同，均为0.2s；经过0.35s即7/4个周期，质点P位于正的最大位移(即波峰)，而质点Q正离开平衡位置向y轴负向运动的过程中，位移还未达到最大值，故A正确；经过0.25s即5/4个周期，质点P处于负向最大位移，而质点Q的位移未达到最大值，而加速度与位移大小成正比，故B正确；根据波速公式v＝ ＝20m/s，根据x＝vt可知C正确；经过0.1s即1/2个周期，质点Q的运动方向沿y轴负方向，故D错误．‎ ‎[答案]　ABC 四、电磁振荡的周期和频率 ‎1．振荡过程中电荷量、电流、电场能和磁场能的变化 在LC回路产生振荡电流的过程中，磁场能和电场能之间不断地相互转化着，电容器放电时，电容器电荷量减小，电流增大，电场能转化为磁场能；放电完毕的瞬间，电荷量为零，电流最大，电场能为零，磁场能转化为电场能；充电完毕的瞬间，电流为零，电荷量达到最大，此时磁场能为零，电场能最大．‎ ‎2．电磁振荡的周期和频率 ‎[例4]　在如图甲所示的LC振荡电路中，通过P点的电流变化规律如图乙所示，且把通过P点向右的电流规定为图乙坐标轴i的正方向，则 (　　)‎ A．0.5s至1s内，电容器在充电 B．0.5s至1s内，电容器的上极板带正电 C．1s至1.5s内，Q点比P点电势高 D．1s至1.5s内，磁场能正在转化为电场能 ‎[解析]　在0.5s至1s内，由图象可以看出，电流方向为正方向，即在LC振荡电路中P点的电流方向向右；由于电流正在减小，故电容器上的电量正在增加，电容器在充电，且下极板带正电．由于P点与电容器上极板等电势，Q点与电容器下极板等电势，故为了比较P，Q两点电势的高低，只要比较电容器上、下极板电势的高低即可．在1s至1.5s内，电流为负方向，在LC回路中P点的电流方向向左；由于电流增大，故电容器正在放电，电容器的电荷量在减少，下极板带正电，故Q点电势比P点电势高，且在此时间内电场能正在向磁场能转化．‎ ‎[答案]　AC 五、电磁场理论的理解与应用 变化的磁场在周围空间激发的电场是涡旋电场，涡旋电场与静电场一样对电荷有力的作用．但涡旋电场又与静电场不同，它不是静电荷产生的，它的电场线是闭合的，在涡旋电场中移动电荷时，电场力做的功与路径有关，因此不能引用“电势”“电势能”等概念，变化的磁场产生电场是电磁感应现象的本质．‎ ‎[例5]‎ ‎　电子感应加速器是利用变化磁场产生的电场来加速电子的，如图所示．在圆形磁铁的两极之间有一环形真空室，用交变电流作电源充磁的电磁铁在两极间产生交变磁场，从而在环形室内产生很强的电场，使电子加速．被加速的电子同时在洛伦兹力的作用下沿圆形轨道运动，设法把高能电子引入靶室，能使其进一步加速．在一个半径为r的电子感应加速器中，电子在被加速的4.2×10－3s时间内获得的能量为120MeV，这期间电子轨道内的高频交变磁场是线性变化的，磁通量从零增到1.8Wb，求：‎ 电子感应加速器结构原理图 ‎(1)电子在环形真空室中共绕行了多少周？‎ ‎(2)有人说，根据麦克斯韦电磁场理论及法拉第电磁感应定律，电子感应加速器要完成电子的加速过程，电子轨道内的高频交变磁场也可以是线性减弱的，效果将完全一样．你同意吗？请简述理由．‎ ‎[解析]　(1)‎ 由麦克斯韦电磁场理论可知，当交变磁场的磁感应强度线性增强时，电子所处的环形真空室内产生感应电动势，该电动势可由法拉第电磁感应定律求得，令其为ε， 则电子在环形真空室中运动一周的过程中被电场加速做功为W0＝εe＝ ×103eV，那么获得120MeV的能量需绕行的周数为 ‎(2)不同意．尽管交变磁场线性减小也可以产生等大的电动势使电子加速，但减小的磁场不能提供越来越大的洛伦兹力以维持做加速运动的电子绕行时所需的向心力．‎ ‎[答案]　(1)2.8×105　(2)见解析 六、光的折射和折射率 ‎1．光的折射定律 折射光线跟入射光线在同一平面内；折射光线和入射光线分别位于法线的两侧；入射角的正弦跟折射角的正弦成正比，即＝ n.‎ 在光的折射现象中，光路也是可逆的．‎ ‎2．折射率 光从真空射入某种介质，入射角的正弦与折射角正弦之比为定值，叫做介质的折射率，表示为n＝ .‎ 实验和研究证明，某种介质的折射率等于光在真空中的速度c跟光在这种介质中的速度v之比，即n＝ .‎ 同一种介质，对频率越高的光，折射率越大，这是光的色散现象形成的根本原因．‎ ‎3．全反射和临界角 全反射的条件：①光从光密介质进入光疏介质；②入射角大于或等于临界角．‎ 临界角：折射角等于90°时的入射角，某种介质的临界角用sinC＝ 计算．‎ ‎[例6]　如图所示，AOB是由某种透明物质制成的1/4圆柱体的横截面(O为圆心)，其折射率为，今有一束平行光以45°的入射角射向柱体的OA平面，这些光线中有一部分不能从柱体的AB面上射出．设所有射到OB面的光线全部被吸收，也不考虑OA面的反射，求圆柱AB面上能射出光线的部分占AB表面的几分之几？并在图中用阴影部分标示．‎ ‎[解析]　作出光路如右图所示，从O点射入的光线，折射角为r，根据折射定律有：‎ 解得r＝30°‎ 从某位置P点入射的光线，折射到AB弧面上Q点时，入射角恰等于临界角C，有：‎ 代入数据得：C＝45°‎ ‎△PQO中，α＝180°－90°－r－C＝15°‎ 所以能射出的光线区域对应的圆心角 β＝90°－α－r＝45°‎ 故能射出光线的部分占AB面的比例为：‎ 图中阴影部分为能射出光线的区域．‎ ‎[答案]　‎ 七、全反射和临界角 ‎1．全反射 ‎(1)现象：光经过两种不同介质的界面时全部反射，不发生折射的现象．‎ ‎(2)条件：①光从光密介质射入光疏介质．②入射角大于等于临界角．‎ ‎2．临界角：sinC＝ ，C为折射角等于90°时的入射角．‎ ‎[例7]　如图所示，置于空气中的一不透明容器内盛满某种透明液体．容器底部靠近器壁处有一竖直放置的6.0cm长的线光源．靠近线光源一侧的液面上盖有一遮光板，另一侧有一水平放置的与液面等高的望远镜，用来观察线光源．开始时通过望远镜不能看到线光源的任何一部分．将线光源沿容器底向望远镜一侧平移至某处时，通过望远镜刚好可以看到线光源底端，再将线光源沿同一方向移动8.0cm，刚好可以看到其顶端．求此液体的折射率n.‎ ‎[解析]　若线光源底端在A点时，望远镜内刚好可看到线光源的底端，则有：‎ ‎∠AOO′＝α 其中α为此液体到空气的全反射临界角，由折射定律得：sinα＝‎ 同理，线光源顶端在B1点时，望远镜内刚好可看到线光源的顶端，则：∠B1OO′＝α 由图中几何关系得：sinα＝‎ ‎[答案]　1.3‎