2020届高三物理二轮 三轮总复习重点 图象法 逆向法 临界法 整体与隔离法突破课后限时练

2020届高三物理二轮 三轮总复习重点 图象法 逆向法 临界法 整体与隔离法突破课后限时练

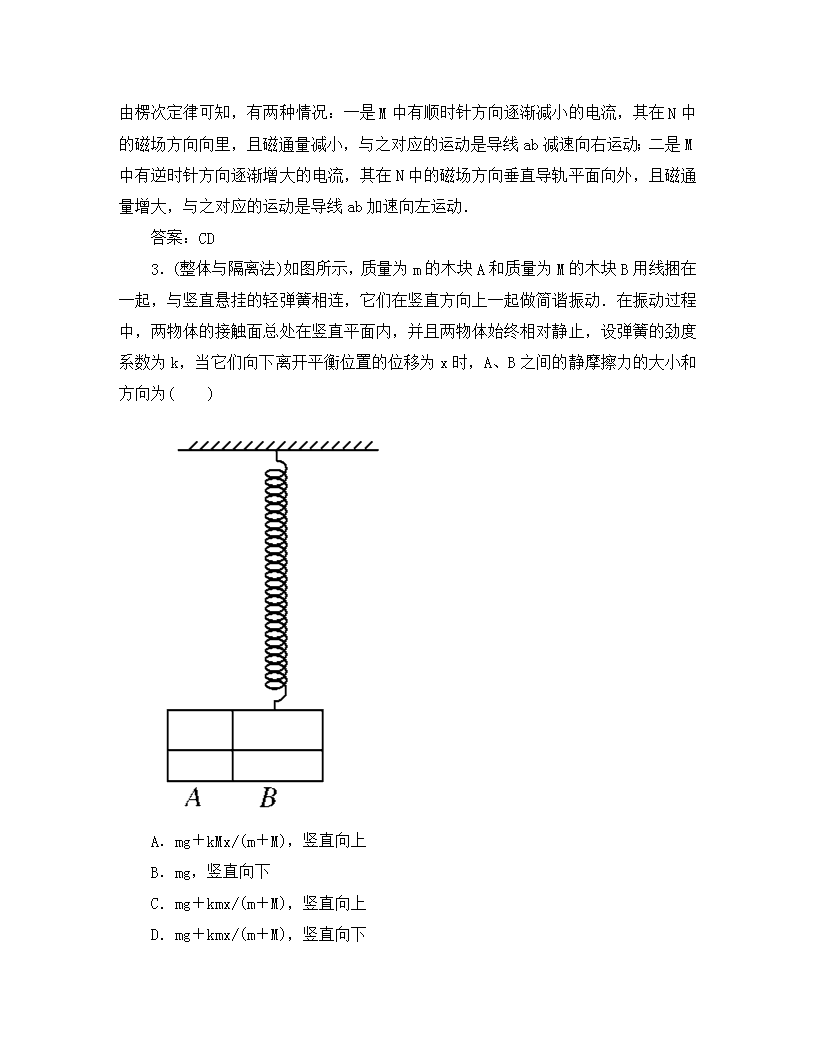
课后限时练（二十三）　 图象法、逆向法、临界法、整体与隔离法 ‎ ‎1.(图象法)如图所示，将质量为‎2m的长木板静止放在光滑的水平面上，一质量为m的小铅块(可视为质点)以水平初速度v0由木板左端滑上恰在木板的右端与木板相对静止，铅块运动过程中所受摩擦力始终不变．现将木板分成长度和质量均相等的两段后紧挨着仍放在水平面上，让小铅块仍以相同的初速度由左端开始滑动，则小铅块将(　　)‎ A．滑到右端与木板保持相对静止 B．在滑到右端前就与木板保持相对静止 C．滑过右端后飞离木板 D．以上答案均有可能 解析：本题用常规方法，运算十分繁杂．考虑到本题中各物体均做匀变速直线运动，且要求讨论相对位移，而v－t图中很容易找到相对位移，所以用图像法处理则变得非常简捷明了．先画出铅块和木板的速度图像如图所示．第一次：‎ v‎0A表示铅块的速度图像，OA表示木板的速度图像；图像包围的“面积”即△v0OA的“面积”为铅块相对木板的位移，即为木板长L.第二次：v0B表示铅块的速度图像，OC表示铅块在前一半木板上运动时后一半木板的速度图像(加速度和第一次一样)，CB表示铅块在后一半木板上运动时后一半木板的速度图像(加速度比第一次大)；图像包围的“面积”即v0BCO的“面积”为铅块相对木板的位移，由图可知该位移小于木板长L，故铅块未滑到木板右端就相对木板静止．‎ 答案：B ‎2．(逆向法)在匀强磁场中放一电阻不计的平行金属导轨，导轨跟大线圈M相接，如图所示．导轨上放一根导线ab，磁感线垂直于导轨所在平面向外．欲使M内的小闭合线圈N产生顺时针方向的感应电流，则导线的运动可能是(　　)‎ A．匀速向右运动　　　　B．加速向右运动 C．减速向右运动 D．加速向左运动 解析：N中产生顺时针方向的感应电流，则N中的磁场方向必定垂直纸面向里，由楞次定律可知，有两种情况：一是M中有顺时针方向逐渐减小的电流，其在N中的磁场方向向里，且磁通量减小，与之对应的运动是导线ab减速向右运动；二是M中有逆时针方向逐渐增大的电流，其在N中的磁场方向垂直导轨平面向外，且磁通量增大，与之对应的运动是导线ab加速向左运动．‎ 答案：CD ‎3．(整体与隔离法)如图所示，质量为m的木块A和质量为M的木块B用线捆在一起，与竖直悬挂的轻弹簧相连，它们在竖直方向上一起做简谐振动．在振动过程中，两物体的接触面总处在竖直平面内，并且两物体始终相对静止，设弹簧的劲度系数为k，当它们向下离开平衡位置的位移为x时，A、B之间的静摩擦力的大小和方向为(　　)‎ A．mg＋kMx/(m＋M)，竖直向上 B．mg，竖直向下 C．mg＋kmx/(m＋M)，竖直向上 D．mg＋kmx/(m＋M)，竖直向下 解析：当A、B向下离开平衡位置的位移为x时，它们具有竖直向上的加速度a，将A、B视为整体由牛顿第二定律有a＝kx/(m＋M)，此时木块A由重力mg和A、B之间的静摩擦力f的合力来提供回复力，则合外力的方向竖直向上，对木块A由牛顿第二定律有f－mg＝ma，解得f＝mg＋kmx/(m＋M)．‎ 答案：C ‎4．(图象法)总质量为M的列车，沿水平直线轨道匀速前进，其末节车厢质量为m，中途脱节，司机发现时，机车已行驶距离L，于是撤去牵引力．设运动的阻力与重力成正比，机车牵引力是恒定的，求当列车的两部分都停止时，它们之间的距离为多少？‎ 解析：本题解题方法很多，但用图像法解简单明了．如图所示，脱节后末节车厢做匀减速直线运动，加速度为am＝kg；前部分列车先做匀加速直线运动，加速度为a1＝kmg/(M－m)，后做匀减速直线运动，加速度为a2＝k(M－m)g/(M－m)＝kg.由图像知：末节车厢从脱节到停止的位移为△OvD的“面积”；而前部分列车从脱节到停止的位移为四边形OvAC的“面积”．因△OvD和△EBC“面积”相等，所以两部分都停止时之间的距离s为五边形OvABE的“面积”．又a1t1＝a2t2，所以t1/t2＝(M－m)/m，由题意知四边形OvAF的“面积”为L，则：L/s＝t1/(t1＋t2)，故s＝L(t1＋t2)/t1＝ML(M－m)．‎ ‎5．(逆向法)一物体以某一初速度在粗糙水平面上做匀减速直线运动最后停下来，若此物体在最初5 s和最后5 s经过的路程之比为115，则此物体一共运动了多长时间？‎ 解析：若按常规思维方式即“从条件推结论”的思维方式，应根据匀变速直线运动规律列式，这必会碰到总时间t比前后两个5 s之和10 s大还是小的问题：若t>10 s，将时间分为前5 s和后5 s与中间的时间t2，经复杂运算得t2＝－2 s，再得出t＝8 s的结论．如果采用逆向思维，将物体的运动按时间先后顺序颠倒过来看，即物体的运动看做是逆向的初速度为零的匀加速直线运动处理，将会简捷得多．‎ 设物体运动总时间为t，最后5 s通过的路程为s2，则：s2＝at2－a(t－5)2＝5at－12.5a 最初5 s通过的路程为s1，则：s1＝a·52＝12.5a 由题中已知的条件：s2s1＝115‎ 解得运动时间t＝8 s.‎ ‎6．(整体与隔离法)如图所示，表面光滑的平行金属导轨P、Q水平放置，左端与一电动势为E，内阻为r的电源连接，导轨间距为d，电阻不计，导轨上放有两根质量均为m的细棒，棒Ⅰ的电阻为R，棒Ⅱ为绝缘体，两棒之间用一轻杆相连．导轨所在空间有垂直导轨平面向外的匀强磁场，磁感应强度大小为B.求：‎ ‎(1)闭合开关S瞬间棒Ⅱ的加速度；‎ ‎(2)从闭合开关S到两棒速度达到v的过程中，通过棒Ⅰ的电荷量和电源消耗的总能量分别为多少？(导轨足够长，且不考虑电磁辐射)‎ 解析：(1)闭合开关S瞬间，电路中的电流为I＝ 棒Ⅰ受的安培力F＝BId= 对棒Ⅰ、棒Ⅱ整体，根据牛顿第二定律得a＝＝，方向水平向左．‎ ‎(2)对棒Ⅰ、棒Ⅱ整体，由动量定理得BI′dt＝2mv，又q＝I′t 所以q＝，电源消耗的总能量为E能＝qE＝.‎ ‎7．(临界法)如图所示，光滑水平面右端B处连接一个竖直的半径为R的光滑半圆轨道，在距离B为x处的A点，用水平恒力将质量为m的小球从静止开始推到B处后撤去恒力，小球沿半圆轨道运动到C处后又正好落回A点，求：‎ ‎(1)推力对小球所做的功．‎ ‎(2)x取何值时，完成上述运动力F所做的功最小？最小功为多少？‎ ‎(3)x取何值时，完成上述运动力F最小？最小力为多少？‎ 解析：(1)小球从半圆轨道C点做平抛运动又回到A点，设小球在C点的速度为v0，小球从C点运动到A点所用的时间为t 在水平方向上x＝v0t 竖直方向上2R＝gt2‎ 对小球从A到C过程由动能定理有WF－mg·2R＝mv 解得WF＝.‎ ‎(2)要使力F做功最小，从而确定x的取值，只要小球在C点速度最小，则功WF就最小，若小球恰好能通过C点，其在C点最小速度为v，由牛顿第二定律有 mg＝，则v＝ 由平抛运动规律可知x＝vt,2R＝gt2‎ 则x＝·＝2R 由WF－2mgR＝mv2可得WF＝mgR.‎ ‎(3)由W＝Fx和WF＝ 得F＝mg(＋)‎ 当＝，即x＝4R时，＋＝8‎ 最小力F＝mg. ‎