开普勒运动的可能轨道与宇宙速度

开普勒运动的可能轨道与宇宙速度

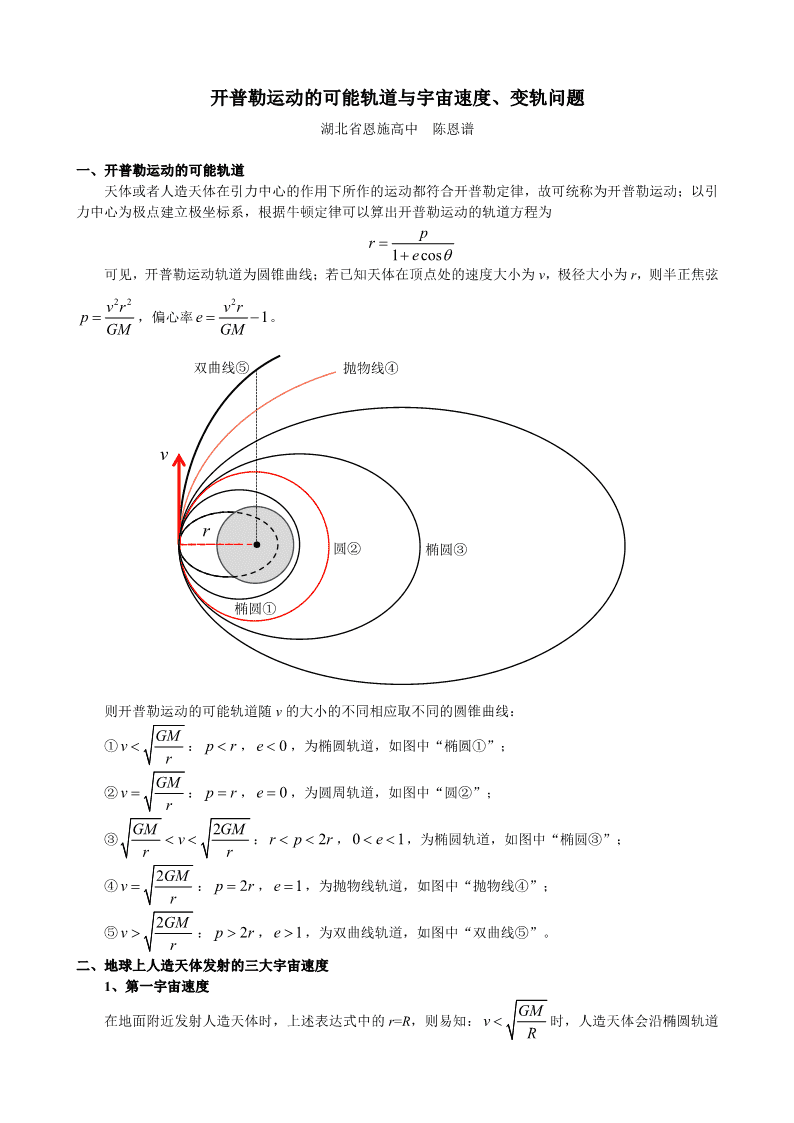
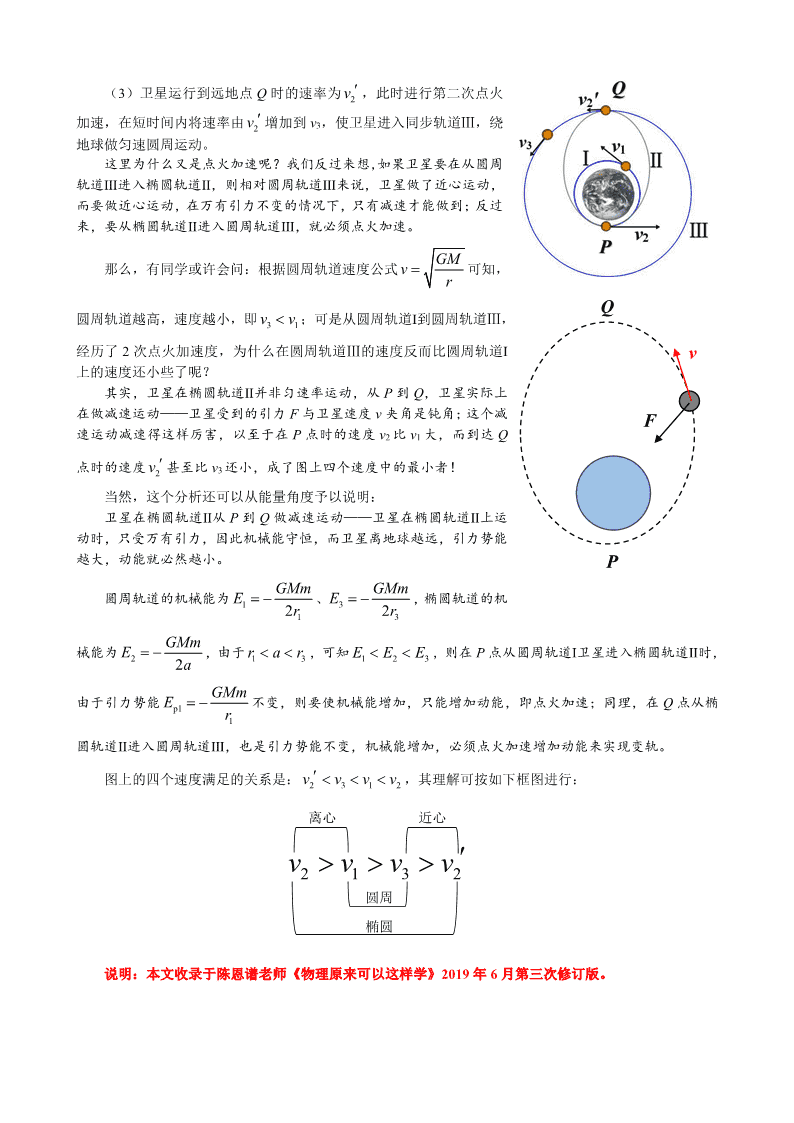
开普勒运动的可能轨道与宇宙速度、变轨问题 湖北省恩施高中 陈恩谱 一、开普勒运动的可能轨道 天体或者人造天体在引力中心的作用下所作的运动都符合开普勒定律，故可统称为开普勒运动；以引 力中心为极点建立极坐标系，根据牛顿定律可以算出开普勒运动的轨道方程为 1 cos pr e   可见，开普勒运动轨道为圆锥曲线；若已知天体在顶点处的速度大小为 v，极径大小为 r，则半正焦弦 2 2v rp GM  ，偏心率 2 1v re GM   。 则开普勒运动的可能轨道随 v 的大小的不同相应取不同的圆锥曲线： ① GMv r  ： p r ， 0e  ，为椭圆轨道，如图中“椭圆①”； ② GMv r  ： p r ， 0e  ，为圆周轨道，如图中“圆②”； ③ 2GM GMvr r   ： 2r p r  ， 0 1e  ，为椭圆轨道，如图中“椭圆③”； ④ 2GMv r  ： 2p r ， 1e  ，为抛物线轨道，如图中“抛物线④”； ⑤ 2GMv r  ： 2p r ， 1e  ，为双曲线轨道，如图中“双曲线⑤”。 二、地球上人造天体发射的三大宇宙速度 1、第一宇宙速度 在地面附近发射人造天体时，上述表达式中的 r=R，则易知： GMv R  时，人造天体会沿椭圆轨道 · v r 圆② 椭圆③ 椭圆① 抛物线④双曲线⑤ 回到地面，无法发射升空；只有 GMv R ≥ 时，才可能发射升空，因此把 GMv R Ⅰ 称之为第一宇宙速度， 即人造天体升空的最小发射速度。 2、第二宇宙速度 但是，如果 2 = 2GMv vR Ⅰ≥ ，则人造天体将沿椭圆、双曲线轨道运动，这就会运动到“无穷远处” 而脱离地球引力的束缚；所以，把 2 = 2GMv vR Ⅱ Ⅰ称之为第二宇宙速度。 3、第三宇宙速度 当地面附近发射人造天体的（相对地球）速度 2= GMv R 时， 人造天体将（相对地球）沿抛物线轨道运动到离地球“无穷远处” 而相对地球静止——实际上是运动到地球绕太阳的公转轨道上， 与地球同步绕太阳“公转”；若在地面附近发射人造天体的（相 对地球）速度过大（超过 vⅢ ），将导致人造天体在地球绕太阳 公转轨道上的相对太阳的速度超过地球公转速度的 2 倍（即 2v v地≥ ），则人造天体将相对太阳以抛物线、双曲线运动到 离太阳的“无穷远处”，即脱离太阳引力的束缚，逃出太阳系。 这个相对地球的速度 vⅢ 就被称作第三宇宙速度，其计算涉及到参考系转换问题，就不在此赘述。 下图即牛顿的人造卫星设想图。 三、人造卫星的变轨问题 如右图所示，发射同步卫星时， （1）通常先将卫星发送到近地轨道Ⅰ，使其绕地球做匀速圆周运动，速率为 v1； （2）第一次在 P 点点火加速，在短时间内将速率由 v1 增加到 v2，使卫星进入椭圆形的转移轨道Ⅱ； 这里为什么要点火加速呢？因为在 P 点，要使从圆周轨道Ⅰ卫星进入椭圆轨道Ⅱ，相对圆周轨道来说， 卫星做了离心运动，而要做离心运动，在万有引力不变的情况下，只有加速才能做到。 （3）卫星运行到远地点 Q 时的速率为 2v  ，此时进行第二次点火 加速，在短时间内将速率由 2v  增加到 v3，使卫星进入同步轨道Ⅲ，绕 地球做匀速圆周运动。 这里为什么又是点火加速呢？我们反过来想，如果卫星要在从圆周 轨道Ⅲ进入椭圆轨道Ⅱ，则相对圆周轨道Ⅲ来说，卫星做了近心运动， 而要做近心运动，在万有引力不变的情况下，只有减速才能做到；反过 来，要从椭圆轨道Ⅱ进入圆周轨道Ⅲ，就必须点火加速。 那么，有同学或许会问：根据圆周轨道速度公式 GMv r  可知， 圆周轨道越高，速度越小，即 3 1v v ；可是从圆周轨道Ⅰ到圆周轨道Ⅲ， 经历了 2 次点火加速度，为什么在圆周轨道Ⅲ的速度反而比圆周轨道Ⅰ 上的速度还小些了呢？ 其实，卫星在椭圆轨道Ⅱ并非匀速率运动，从 P 到 Q，卫星实际上 在做减速运动——卫星受到的引力 F 与卫星速度 v 夹角是钝角；这个减 速运动减速得这样厉害，以至于在 P 点时的速度 v2 比 v1 大，而到达 Q 点时的速度 2v  甚至比 v3 还小，成了图上四个速度中的最小者！ 当然，这个分析还可以从能量角度予以说明： 卫星在椭圆轨道Ⅱ从 P 到 Q 做减速运动——卫星在椭圆轨道Ⅱ上运 动时，只受万有引力，因此机械能守恒，而卫星离地球越远，引力势能 越大，动能就必然越小。 圆周轨道的机械能为 1 12 GMmE r   、 3 32 GMmE r   ，椭圆轨道的机 械能为 2 2 GMmE a   ，由于 1 3r a r  ，可知 1 2 3E E E  ，则在 P 点从圆周轨道Ⅰ卫星进入椭圆轨道Ⅱ时， 由于引力势能 p1 1 GMmE r   不变，则要使机械能增加，只能增加动能，即点火加速；同理，在 Q 点从椭 圆轨道Ⅱ进入圆周轨道Ⅲ，也是引力势能不变，机械能增加，必须点火加速增加动能来实现变轨。 图上的四个速度满足的关系是： 2 3 1 2v v v v    ，其理解可按如下框图进行： 说明：本文收录于陈恩谱老师《物理原来可以这样学》2019 年 6 月第三次修订版。 离心 近心 圆周 椭圆 2 1 3 2v v v v    v F P Q