2020-2021年高三物理考点专项突破：整体与隔离法在两种力学状态下的应用规律

2020-2021年高三物理考点专项突破：整体与隔离法在两种力学状态下的应用规律

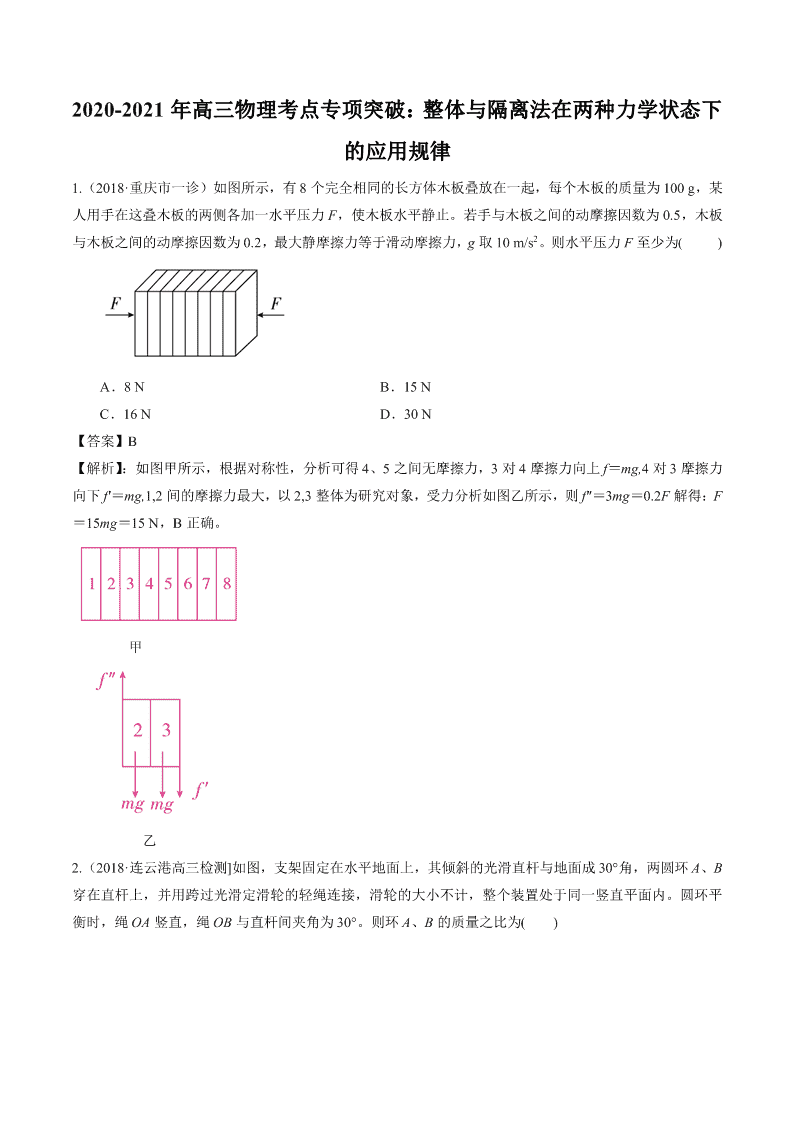
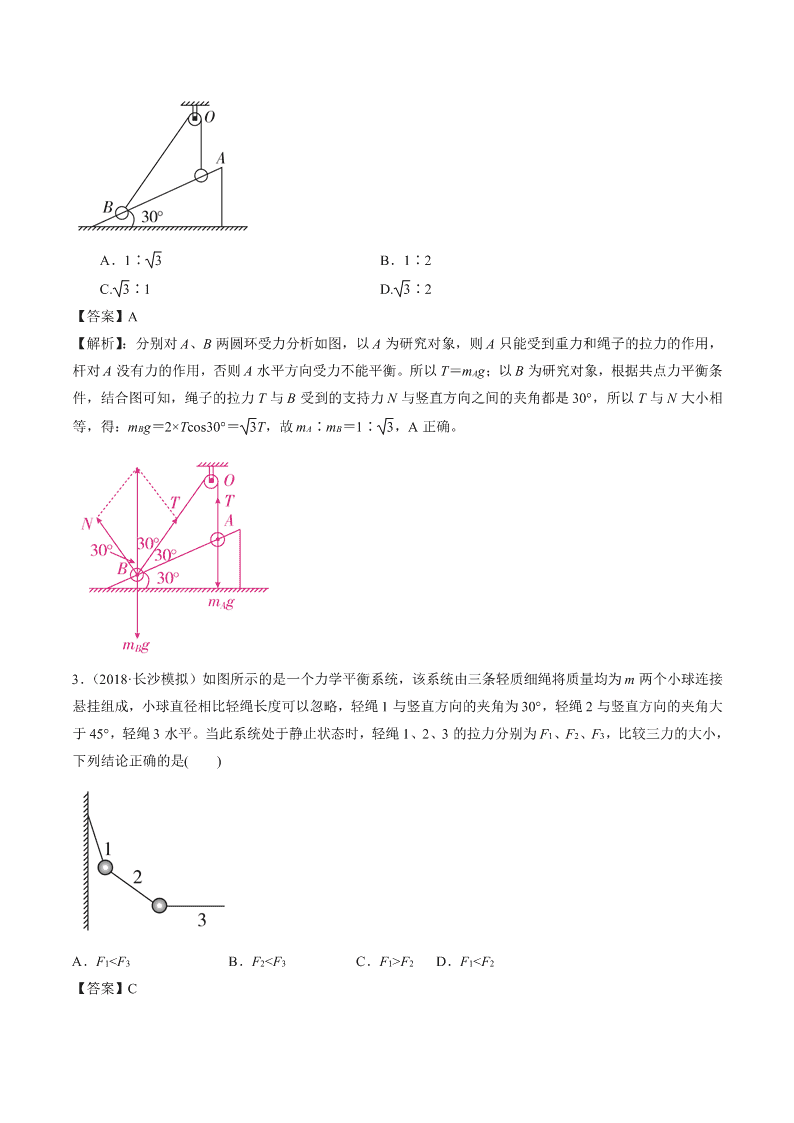
2020-2021 年高三物理考点专项突破：整体与隔离法在两种力学状态下 的应用规律 1.（2018·重庆市一诊）如图所示，有 8 个完全相同的长方体木板叠放在一起，每个木板的质量为 100 g，某 人用手在这叠木板的两侧各加一水平压力 F，使木板水平静止。若手与木板之间的动摩擦因数为 0.5，木板 与木板之间的动摩擦因数为 0.2，最大静摩擦力等于滑动摩擦力，g 取 10 m/s2。则水平压力 F 至少为( ) A．8 N B．15 N C．16 N D．30 N 【答案】B 【解析】：如图甲所示，根据对称性，分析可得 4、5 之间无摩擦力，3 对 4 摩擦力向上 f＝mg,4 对 3 摩擦力 向下 f′＝mg,1,2 间的摩擦力最大，以 2,3 整体为研究对象，受力分析如图乙所示，则 f″＝3mg＝0.2F 解得：F ＝15mg＝15 N，B 正确。 甲 乙 2.（2018·连云港高三检测]如图，支架固定在水平地面上，其倾斜的光滑直杆与地面成 30°角，两圆环 A、B 穿在直杆上，并用跨过光滑定滑轮的轻绳连接，滑轮的大小不计，整个装置处于同一竖直平面内。圆环平 衡时，绳 OA 竖直，绳 OB 与直杆间夹角为 30°。则环 A、B 的质量之比为( ) A．1∶ 3 B．1∶2 C. 3∶1 D. 3∶2 【答案】A 【解析】：分别对 A、B 两圆环受力分析如图，以 A 为研究对象，则 A 只能受到重力和绳子的拉力的作用， 杆对 A 没有力的作用，否则 A 水平方向受力不能平衡。所以 T＝mAg；以 B 为研究对象，根据共点力平衡条 件，结合图可知，绳子的拉力 T 与 B 受到的支持力 N 与竖直方向之间的夹角都是 30°，所以 T 与 N 大小相 等，得：mBg＝2×Tcos30°＝ 3T，故 mA∶mB＝1∶ 3，A 正确。 3．（ 2018·长沙模拟）如图所示的是一个力学平衡系统，该系统由三条轻质细绳将质量均为 m 两个小球连接 悬挂组成，小球直径相比轻绳长度可以忽略，轻绳 1 与竖直方向的夹角为 30°，轻绳 2 与竖直方向的夹角大 于 45°，轻绳 3 水平。当此系统处于静止状态时，轻绳 1、2、3 的拉力分别为 F1、F2、F3，比较三力的大小， 下列结论正确的是( ) A．F1F2 D．F1F3，A 错误；对下方小球受力分析，因 F2 是直角三角形的斜边，而 mg 和 F3 是直角边，由轻绳 2 与竖直 方向的夹角 θ>45°，可知 F2>F3，B 错误；对上方小球分析，水平方向：F1sin30°＝F2sinθ，因 θ>45°，则 F1>F2， C 正确，D 错误。 4．（ 2017·哈尔滨六中摸底）一个截面是直角三角形的木块放在水平面上，在斜面上放一个光滑球，球的一 侧靠在竖直墙上，木块处于静止，如图所示。若在光滑球的最高点施加一个竖直向下的力 F，球仍处于静止， 则木块对地面的压力 N 和摩擦力 f 的变化情况是( ) A．N 增大 B．f 增大 C．N 不变 D．f 不变 【答案】 AB 【解析】以整体为研究对象受力分析如图甲：施加 F 以后很明显地面对木块的支持力由(M＋m)g 变为(M＋ m)g＋F，则木块对地面的压力 N 变大。水平方向 f＝FN。 隔离球受力如图乙： 竖直方向：F1cosθ＝mg＋F 水平方向：F1sinθ＝FN 由竖直方向知加 F 后 F1 变大，则由水平方向知 FN 变大，联系整体知木块对地面的摩擦力 f 变大，故选 A、 B。 5.(2018·杭州七校联考)如图所示，甲、乙两个小球的质量均为 m，两球间用细线连接，甲球用细线悬挂在天 花板上。现分别用大小相等的力 F 水平向左、向右拉两球，平衡时细线都被拉紧。则平衡时两球的可能位 置是下面的( ) 【答案】： A 【解析】：用整体法分析，把两个小球看作一个整体，此整体受到的外力为竖直向下的重力 2mg、水平向左 的力 F(甲受到的)、水平向右的力 F(乙受到的)和细线 1 的拉力，两水平力相互平衡，故细线 1 的拉力一定 与重力 2mg 等大反向，即细线 1 一定竖直；再用隔离法，分析乙球受力的情况，乙球受到向下的重力 mg， 水平向右的拉力 F，细线 2 的拉力 F2。 要使得乙球受力平衡，细线 2 必须向右倾斜。 6.(10 分)如图所示，质量 M＝2 3 kg 的木块 A 套在水平杆上，并用轻绳将木块 A 与质量 m＝ 3 kg 的小球 B 相连。今用与水平方向成 α＝30°角的力 F＝10 3 N，拉着小球带动木块一起向右匀速运动，运动中 A、B 相对位置保持不变，取 g＝10 m/s2。求： (1)运动过程中轻绳与水平方向夹角 θ； (2)木块与水平杆间的动摩擦因数 μ。 【答案】 (1)30° (2) 3 5 【解析】(1)设轻绳对 B 的拉力为 FT，以小球为研究对象，分析受力，作出受力图如图甲，由平衡条件可得： Fcos30°＝FTcosθ，Fsin30°＋FTsinθ＝mg 代入解得，FT＝10 3 N，tanθ＝ 3 3 ，即 θ＝30°。 (2)以木块和小球组成的整体为研究对象，分析受力情况，如图乙。由平衡条件得 Fcos30°＝Ff FN＋Fsin30°＝(M＋m)g， 又 Ff＝μFN 解得 μ＝ Fcos30° M＋mg－Fsin30°＝ 3 5 。 7.(15 分)所受重力 G1＝8 N 的物块悬挂在绳 PA 和 PB 的结点上。PA 偏离竖直方向 37°角，PB 在水平方向， 且连在所受重力为 G2＝100 N 的木块上，木块静止于倾角为 37°的斜面上，如图所示，试求：(sin53°＝0.8， cos53°＝0.6，重力加速度 g 取 10 m/s2) (1)木块与斜面间的摩擦力大小； (2)木块所受斜面的弹力大小。 【答案】(1)64.8 N (2)76.4 N 【解析】如图甲所示，分析 P 点受力，由平衡条件可得：FAcos37°＝G1，FAsin37°＝FB 可解得：FB＝6 N。 再分析 G2 的受力情况如图乙所示，由平衡条件可得 Ff＝G2sin37°＋FB′cos37°，FN＋FB′sin37°＝G2cos37°， FB′＝FB，可求得 Ff＝64.8 N，FN＝76.4 N。 8.(多选)(2015·新课标全国Ⅱ·20)在一东西向的水平直铁轨上，停放着一列已用挂钩连接好的车厢。当机车在 东边拉着这列车厢以大小为 a 的加速度向东行驶时，连接某两相邻车厢的挂钩 P 和 Q 间的拉力大小为 F； 当机车在西边拉着车厢以大小为2 3a 的加速度向西行驶时，P 和 Q 间的拉力大小仍为 F。不计车厢与铁轨间 的摩擦，每节车厢质量相同，则这列车厢的节数可能为( ) A．8 B．10 C．15 D．18 【答案】： BC 【解析】：设每节车厢的质量为 m，这列车厢的节数为 n，东边车厢的节数为 x，西边车厢的节数为 n－x。 当机车在东边拉车厢时，对西边车厢受力分析，由牛顿第二定律可得 F＝(n－x)·ma；当机车在西边拉车厢 时，对东边车厢受力分析，由牛顿第二定律可得 F＝2 3max，联立可得 n＝5 3x，x 为 3 的倍数，则 n 为 5 的倍 数，选项 B、C 正确，选项 A、D 错误。 9.如图所示，质量分别为 m1、m2 的两个物体通过轻弹簧连接，在力 F 的作用下一起沿水平方向做匀加速直 线运动(m1 在光滑地面上，m2 在空中)。已知力 F 与水平方向的夹角为 θ。则 m1 的加速度大小为( ) A. Fcos θ m1＋m2 B． Fsin θ m1＋m2 C.Fcos θ m1 D．Fsin θ m2 【答案】： A 【解析】：把 m1、m2 看成一个整体，在水平方向上加速度相同，由牛顿第二定律可得 Fcos θ＝(m1＋m2)a， 所以 a＝ Fcos θ m1＋m2 ，选项 A 正确。 10.如图所示，有材料相同的 P、Q 两物块通过轻绳相连，并在拉力 F 作用下沿斜面向上运动，轻绳与拉力 F 的方向均平行于斜面。当拉力 F 一定时，Q 受到绳的拉力( ) A．与斜面倾角 θ 有关 B．与动摩擦因数有关 C．与系统运动状态有关 D．仅与两物块质量有关 【答案】： D 【解析】： 设 P、Q 的质量分别为 m1、m2，Q 受到绳的拉力大小为 FT，物块与斜面间的动摩擦因数为 μ。 根据牛顿第二定律，对整体进行分析，有 F－(m1＋m2)gsin θ－μ(m1＋m2)gcos θ＝(m1＋m2)a；对 Q 进行分析， 有 FT－m2gsin θ－μm2gcos θ＝m2a，解得 FT＝ m2 m1＋m2 F。可见 Q 受到绳的拉力 FT 与斜面倾角 θ、动摩擦因数 μ 和系统运动状态均无关，仅与两物块质量和 F 有关，选项 D 正确。 11.如图甲所示，质量为 m0 的小车放在光滑水平面上，小车上用细线悬吊一质量为 m 的小球，m0>m，用一 力 F 水平向右拉小球，使小球和车一起以加速度 a 向右运动时，细线与竖直方向成 α 角，细线的拉力为 FT。 若用一力 F′水平向左拉小车，使小球和车一起以加速度 a′向左运动时，细线与竖直方向也成 α 角，如图乙 所示，细线的拉力为 FT′。则( ) A．F′＝F，FT′＝FT B．F′>F，FT′＝FT C．F′FT D．F′m，所以 a′>a。对小球与车组成的整体，由牛顿第二定律得 F＝(m0＋m)a，F′＝(m0＋m)a′， 所以 F′>F，选项 B 正确。 12．（ 2017·福建宁德一模）如图所示，质量为 0.2 kg 的物体 A 静止在竖直的轻弹簧上，质量为 0.6 kg 的物 体 B 由细线悬挂在天花板上，B 与 A 刚好接触但不挤压。现将细线突然剪断，则在剪断细线的瞬间 A、B 间 的作用力大小为(g 取 10 m/s2)( ) A．0.5 N B．2.5 N C．0 D．1.5 N 【答案】D 【解析】剪断细线前，A、B 间无压力，则弹簧的弹力 F＝mAg＝2 N，在剪断细线的瞬间，对整体受力分析， 得整体加速度 a＝ mA＋mB g－F mA＋mB ＝7.5 m/s2，对 B 隔离分析有 mBg－FN＝mBa，解得 FN＝mBg－mBa＝1.5 N。 故选 D。 13．（ 2017·盐城月考）一辆小车静止在水平地面上，bc 是固定在车上的一根水平杆，物块 M 穿在杆上，M 通过细线悬吊着小物体 m，m 在小车的水平底板上，小车未动时细线恰好在竖直方向上。现使小车如下图 分四次分别以 a1、a2、a3、a4 的加速度向右匀加速运动，四种情况下 M、m 均与车保持相对静止，且图甲和 图乙中细线仍处于竖直方向，已知 a1∶a2∶a3∶a4＝1∶2∶4∶8，M 受到的摩擦力大小依次为 f1、f2、f3、f4， 则错误的是 ( ) A．f1∶f2＝1∶2 B．f1∶f2＝2∶3 C．f3∶f4＝1∶2 D．tanα＝2tanθ 【答案】 B 【解析】甲、乙图中由于 M 水平方向只受静摩擦力，由牛顿第二定律知 f＝Ma，所以 f1∶f2＝a1∶a2＝1∶2， 故 A 正确、B 错误；丙、丁图中以 M、m 整体为研究对象，由牛顿第二定律有：f＝(M＋m)a，所以 f3∶f4 ＝a3∶a4＝1∶2，故 C 正确；丙、丁图中以 m 为研究对象，由受力分析知受拉力和重力，合力为 F 合＝mgtanθ， 所以 a3∶a4＝tanθ∶tanα，故tanα tanθ＝a4 a3 ＝2 1，即 tanα＝2tanθ，D 正确。 14．（ 2017·长春质监二）如图所示，物块 A、B 质量相等，在恒力 F 作用下，在水平面上做匀加速直线运动。 若物块与水平面间接触面光滑，物块 A 的加速度大小为 a1，物块 A、B 间的相互作用力大小为 N1；若物块 与水平面间接触面粗糙，且物块 A、B 与水平面间的动摩擦因数相同，物块 B 的加速度大小为 a2，物块 A、 B 间的相互作用力大小为 N2，则以下判断正确的是( ) A．a1＝a2 B．a1>a2 C．N1＝N2 D．N13 2μmg 时，A、B 相对地面运动，故 A 错误。对 A、B 整体应用牛顿第二定律，有 F－μ 2×3mg＝3ma；对 B，在 A、B 恰好要发生相对运动时，μ×2mg －μ 2×3mg＝ma，两式联立解得 F＝3μmg，可见，当 F＞3μmg 时，A 相对 B 才能滑动，C 正确。当 F＝5 2μmg 时，A、B 相对静止，对整体有：5 2μmg－μ 2×3mg＝3ma，a＝1 3μg，故 B 正确。无论 F 为何值，B 所受最大的 动力为 A 对 B 的滑动摩擦力 2μmg，故 B 的最大加速度 aBm＝ 2μmg－1 2×3μmg m ＝1 2μg，可见 D 正确。 17.（2017•海南）如图，水平地面上有三个靠在一起的物块 P、Q 和 R，质量分别为 m、2m 和 3m，物块与 地面间的动摩擦因数都为 μ．用大小为 F 的水平外力推动物块 P，R 和 Q 之间相互作用力 F1 与 Q 与 P 之间 相互作用力 F2 大小之比为 k．下列判断正确的是（ ） 5 30: 2 1,0: 5 30: 6 50:     kD kC kB kA 则若 则若 ，则若 ，则若     【答案】:BD 【解析】：将 PQR 看成两部分，PQ 为一部分，R 为一部分，结合结论： QR 之间的力 FF 6 3 1  将 QR 看成一部分，P 看成一部分 PQ 之间的 FF 6 5 2  力： 故 5 3k ，B 正确，又因为 PQR 与水平面间的摩擦因数相同，故 D 也正确；