- 2021-05-26 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【物理】2018届一轮复习人教版法拉第电磁感应定律的理解与应用学案
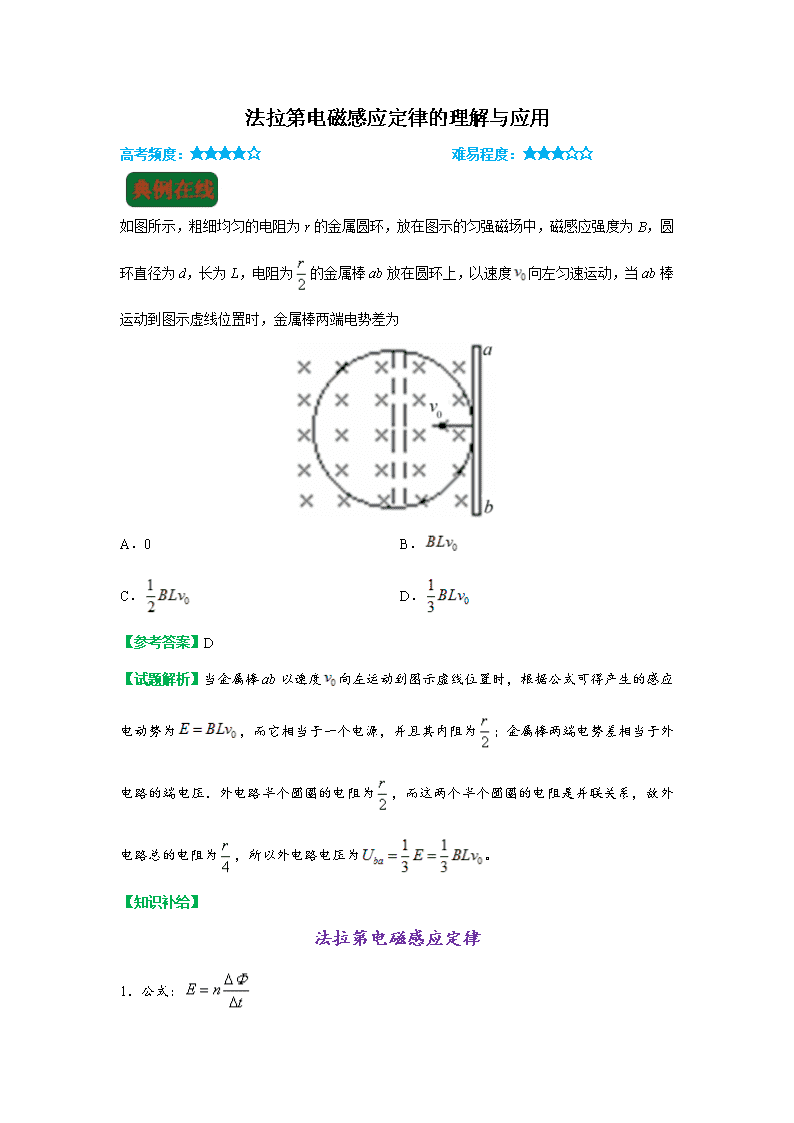
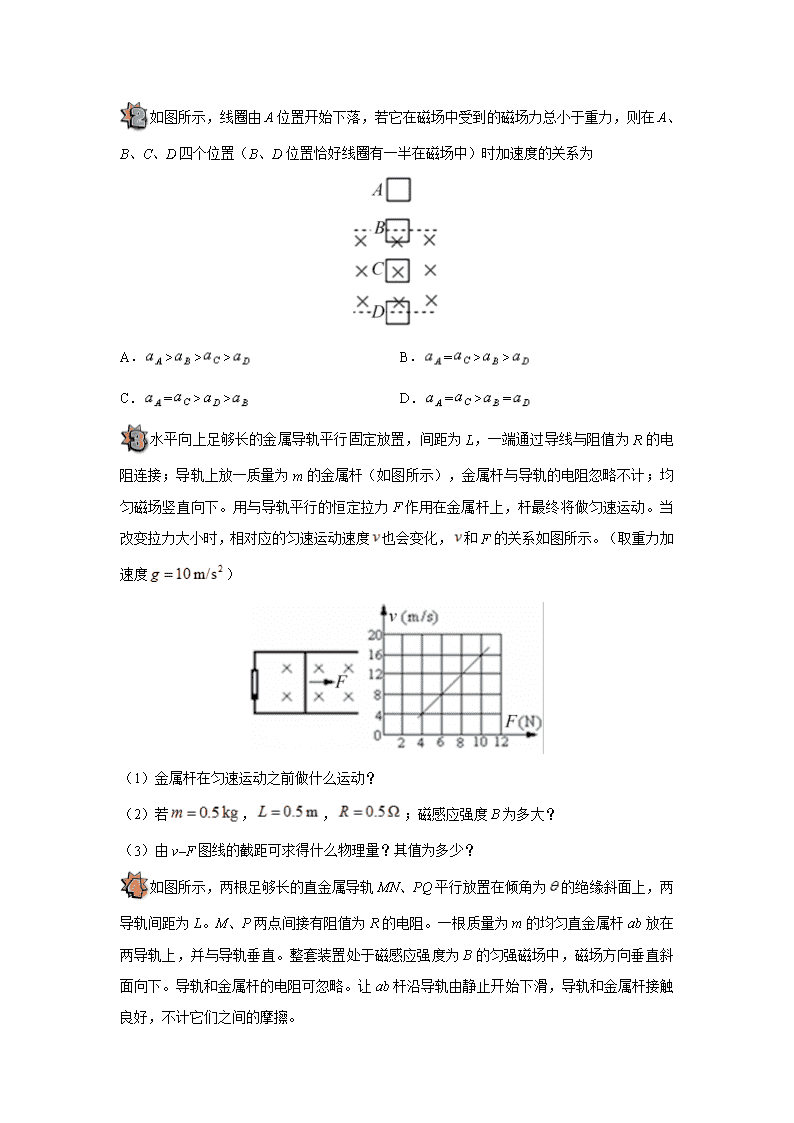
法拉第电磁感应定律的理解与应用 高考频度:★★★★☆ 难易程度:★★★☆☆ 如图所示,粗细均匀的电阻为r的金属圆环,放在图示的匀强磁场中,磁感应强度为B,圆环直径为d,长为L,电阻为的金属棒ab放在圆环上,以速度向左匀速运动,当ab棒运动到图示虚线位置时,金属棒两端电势差为 A.0 B. C. D. 【参考答案】D 【试题解析】当金属棒ab以速度向左运动到图示虚线位置时,根据公式可得产生的感应电动势为,而它相当于一个电源,并且其内阻为;金属棒两端电势差相当于外电路的端电压.外电路半个圆圈的电阻为,而这两个半个圆圈的电阻是并联关系,故外电路总的电阻为,所以外电路电压为。 【知识补给】 法拉第电磁感应定律 1.公式: 2.感应电动势的大小由穿过电路的磁通量的变化率和线圈的匝数共同决定,与磁通量Φ、磁通量的变化量ΔΦ的大小没有必然联系。 3.法拉第发现了电磁感应现象的规律,但法拉第电磁感应定律的数学形式是由纽曼和韦伯给出的。 4.法拉第电磁感应定律的应用 (1)磁通量的变化由磁场变化引起时, 当ΔS=LΔx,且n=1时,公式为导体切割磁感线产生的感应电动势E=BLv (2)磁通量的变化由面积变化引起时, (3)磁通量的变化由磁场和面积变化共同引起时, (4)平均感应电动势 如图所示,一正方形线圈abcd在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动,沿着OO′观察,线圈沿逆时针方向转动。已知匀强磁场的磁感应强度为B,线圈匝数为n,边长为l,电阻为R,转动的角速度为ω。则当线圈转至图示位置时 A.线圈中感应电流的方向为abcda B.线圈中的感应电流为 C.穿过线圈的磁通量为0 D.穿过线圈磁通量的变化率为0 如图所示,线圈由A位置开始下落,若它在磁场中受到的磁场力总小于重力,则在A、B、C、D四个位置(B、D位置恰好线圈有一半在磁场中)时加速度的关系为 A.>>> B.=>> C.=>> D.=>= 水平向上足够长的金属导轨平行固定放置,间距为L,一端通过导线与阻值为R的电阻连接;导轨上放一质量为m的金属杆(如图所示),金属杆与导轨的电阻忽略不计;均匀磁场竖直向下。用与导轨平行的恒定拉力F作用在金属杆上,杆最终将做匀速运动。当改变拉力大小时,相对应的匀速运动速度也会变化,和F的关系如图所示。(取重力加速度) (1)金属杆在匀速运动之前做什么运动? (2)若,,;磁感应强度B为多大? (3)由v–F图线的截距可求得什么物理量?其值为多少? 如图所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为的绝缘斜面上,两导轨间距为L。M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直。整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下。导轨和金属杆的电阻可忽略。让ab杆沿导轨由静止开始下滑,导轨和金属杆接触良好,不计它们之间的摩擦。 (1)由b向a方向看到的装置如图示,请在此图中画出ab杆下滑过程中某时刻的受力示意图; (2)在加速下滑的过程中,当ab杆的速度大小为v时,求此时ab杆中的电流及其加速度的大小; (3)求在下滑过程中,ab杆可以达到的速度最大值。 如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1 m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直,质量为0.2 kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25。 (1)求金属棒沿导轨由静止开始下滑时的加速度大小; (2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8 W,求该速度的大小; (3)在上问中,若R=2 Ω,金属棒中的电流方向由a到b,求磁感应强度的大小与方向。 (g取10 m/s2,sin 37°=0.6,cos 37°=0.8) 【参考答案】 1. BC 2. B(1)金属棒在匀速运动之前做变速运动(加速度越来越小) (2)B=1 T (3)v–F图线的截距可求得金属棒与导轨间的摩擦力,大小为2 N (1)若金属棒与导轨间是光滑的,那么平衡时必有恒定拉力与安培力平衡,即 从而得到,即与F成线性关系且经过坐标原点.而本题的图象坐标没有经过原点,说明金属棒与导轨间有摩擦.金属棒在匀速运动之前,随着速度的增加,安培力越来越大,最后相等。故金属棒在匀速运动之前做变速运动(加速度越来越小) (2)设摩擦力为,平衡时有。选取两个平衡状态,得到两个方程组,从而求解得到。如当F=4 N时,;当F=10 N时,。代入 解得:B=1 T, (3)由以上分析得到:v–F图线的截距可求得金属棒与导轨间的摩擦力,大小为2 N 培力为 根据牛顿第二定律得 即 (3)当加速度为零时速度达到最大即 (1)4 m/s2 (2)10 m/s (3)0.4 T 方向垂直导轨平面向上 (1)金属棒开始下滑的初速度为零,根据牛顿第二定律得 mgsin θ–μmgcos θ=ma① xk.w 由①式解得 a=10×(0.6–0.25×0.8) m/s2=4 m/s2② (2)设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向受力平衡 mgsin θ–μmgcos θ–F=0③ 此时金属棒克服安培力做功的功率等于电路中电阻R消耗的电功率Fv=P④ 由⑥⑦两式解得: B== T=0.4 T⑧ 磁场方向垂直导轨平面向上 查看更多