【物理】2018届二轮复习绳、杆、桥类模型的临界问题学案（全国通用）

【物理】2018届二轮复习绳、杆、桥类模型的临界问题学案（全国通用）

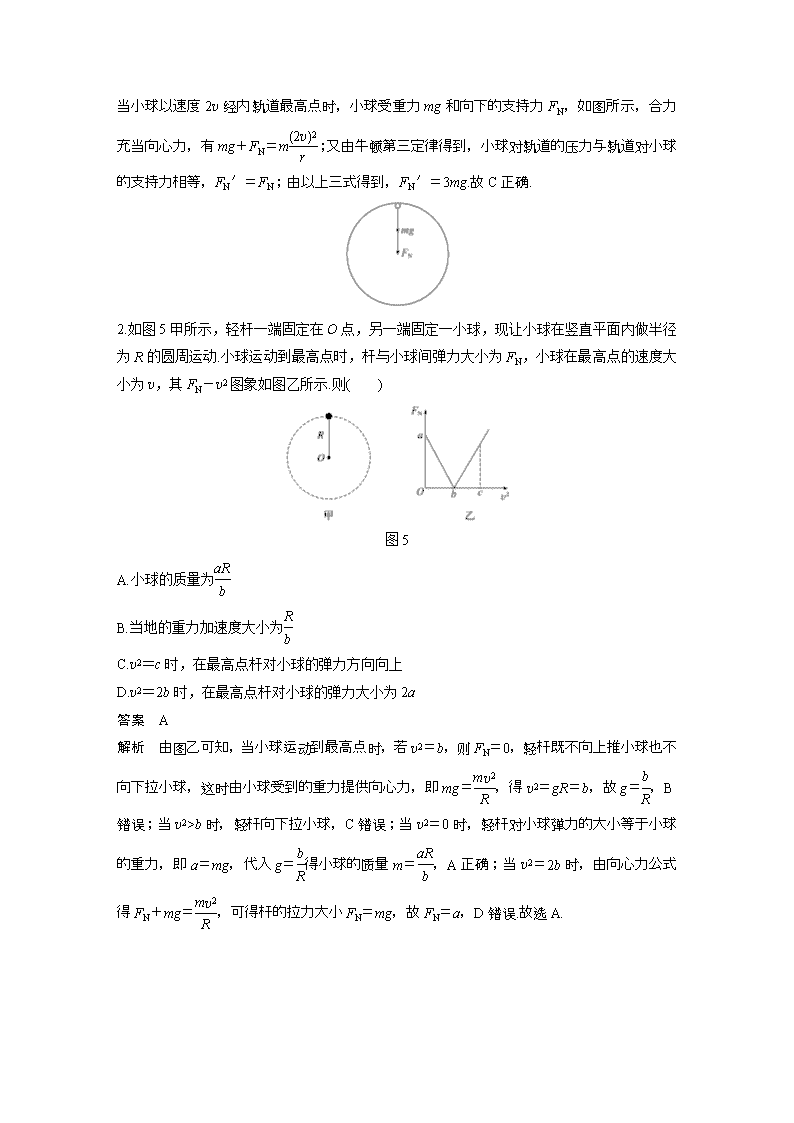
第9点　绳、杆、桥类模型的临界问题 对于物体在竖直平面内做变速圆周运动的问题，中学物理中只研究物体通过最高点和最低点时的情况，并且经常出现临界状态.这类问题常出现在绳、杆、桥类模型的临界问题中.‎ ‎1.类绳模型 ‎(1)此类模型的施力特点：只能提供指向圆心的力.‎ ‎(2)常见的装置：①用绳系物体(如图1甲所示)；②物体沿轨道内侧做圆周运动(如图乙所示).‎ 图1‎ ‎(3)临界特点：此种情况下，如果物体恰能通过最高点，绳子的拉力或轨道对物体的支持力等于零，只有重力提供向心力，即mg＝，得临界速度v0＝.当物体的速度不小于v0时，才能通过最高点.‎ ‎2.类杆模型 ‎(1)此类模型的施力特点：对物体既能提供指向圆心的力，又能提供背离圆心的力.‎ ‎(2)常见的装置：①用杆固定的物体(如图2甲所示)；②小球在光滑圆管中(如图乙所示)；③小球穿在光滑圆环上(如图丙所示).‎ 图2‎ ‎(3)临界特点：此种情况下，由于物体所受的重力可以由杆、管或环对它的向上的支持力来平衡，所以在最高点时的速度可以为零.当物体在最高点的速度v≥0时，物体就可以完成一个完整的圆周运动.‎ ‎3.拱桥模型 ‎(1)此类模型的施力特点：对物体只提供背离圆心的力.‎ ‎(2)常见装置：①拱形桥(如图3甲所示)；②凹凸不平的路面的凸处(如图乙所示).‎ ‎　　　　‎ 图3‎ ‎(3)临界特点：此时，如果物体的速度过大，将会脱离圆轨道而做平抛运动.同样，当轨道对物体的支持力等于零时，是物体做圆周运动的临界情况，即v0＝为临界速度.所以只有当物体的速度小于时，它才能沿轨道外侧做圆周运动.‎ 对点例题　(多选)用细绳拴着质量为m的小球，在竖直平面内做半径为R的圆周运动，如图 图4‎ ‎4所示.则下列说法正确的是(　　)‎ A.小球通过最高点时，绳子张力可以为0‎ B.小球通过最高点时的最小速度为0‎ C.小球刚好通过最高点时的速度是 D.小球通过最高点时，绳子对小球的作用力可以与小球所受重力方向相反 解题指导　设小球通过最高点时的速度为v，由合力提供向心力及牛顿第二定律得mg＋FT＝m.‎ 当FT＝0时，v＝，故选项A正确；‎ 当v＜时，FT＜0，而绳子只能产生拉力，‎ 不能产生与重力方向相反的支持力，故选项B、D错误；‎ 当v＞时，FT＞0，‎ 小球能沿圆弧通过最高点.可见，‎ v≥是小球能沿圆弧通过最高点的条件.‎ 答案　AC ‎1.质量为m的小球在竖直平面内的圆形轨道内侧运动，若经最高点不脱离轨道的临界速度为v，则当小球以2v速度经过最高点时，小球对轨道的压力大小为(　　)‎ A.0 B.mg C.3mg D.5mg 答案　C 解析　当小球以速度v经内轨道最高点时，小球仅受重力，重力充当向心力，有mg＝m 当小球以速度2v经内轨道最高点时，小球受重力mg和向下的支持力FN，如图所示，合力充当向心力，有mg＋FN＝m；又由牛顿第三定律得到，小球对轨道的压力与轨道对小球的支持力相等，FN′＝FN；由以上三式得到，FN′＝3mg.故C正确.‎ ‎2.如图5甲所示，轻杆一端固定在O点，另一端固定一小球，现让小球在竖直平面内做半径为R的圆周运动.小球运动到最高点时，杆与小球间弹力大小为FN，小球在最高点的速度大小为v，其FN－v2图象如图乙所示.则(　　)‎ 图5‎ A.小球的质量为 B.当地的重力加速度大小为 C.v2＝c时，在最高点杆对小球的弹力方向向上 D.v2＝2b时，在最高点杆对小球的弹力大小为2a 答案　A 解析　由图乙可知，当小球运动到最高点时，若v2＝b，则FN＝0，轻杆既不向上推小球也不向下拉小球，这时由小球受到的重力提供向心力，即mg＝，得v2＝gR＝b，故g＝，B错误；当v2>b时，轻杆向下拉小球，C错误；当v2＝0时，轻杆对小球弹力的大小等于小球的重力，即a＝mg，代入g＝得小球的质量m＝，A正确；当v2＝2b时，由向心力公式得FN＋mg＝，可得杆的拉力大小FN＝mg，故FN＝a，D错误.故选A.‎