【物理】2020届二轮复习专题一第1讲　力与物体的平衡学案（京津鲁琼专用）

【物理】2020届二轮复习专题一第1讲　力与物体的平衡学案（京津鲁琼专用）

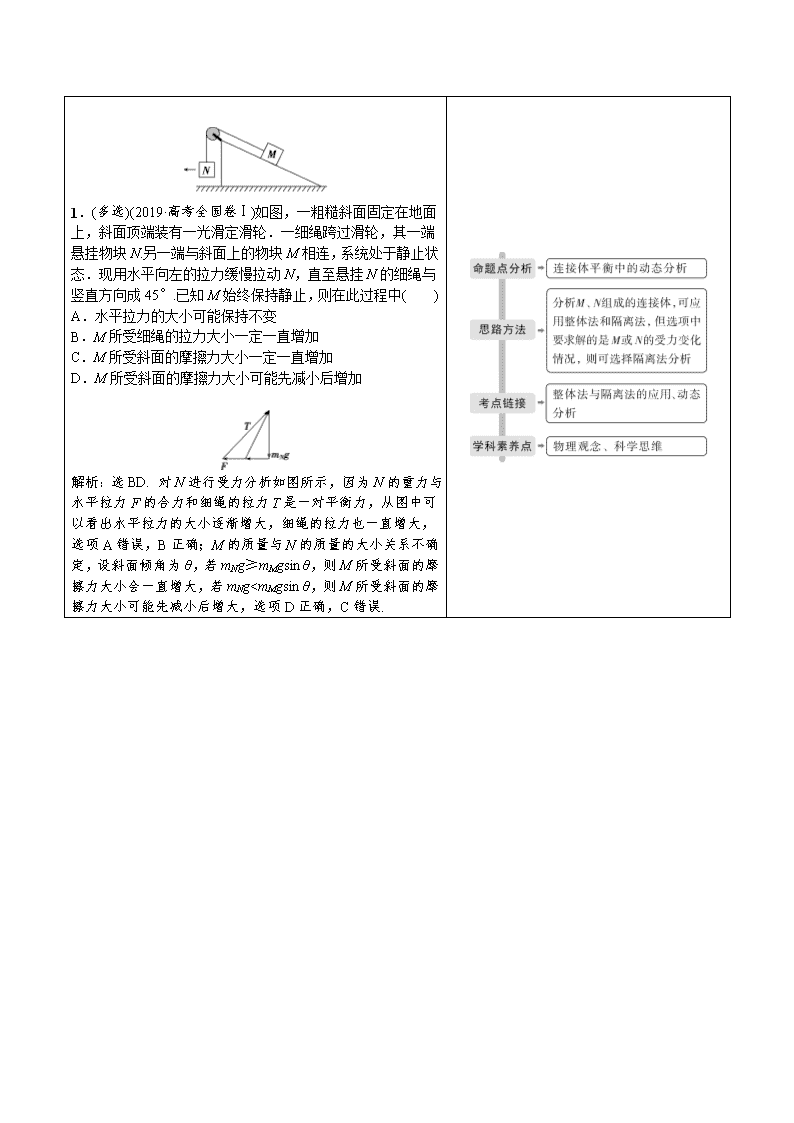
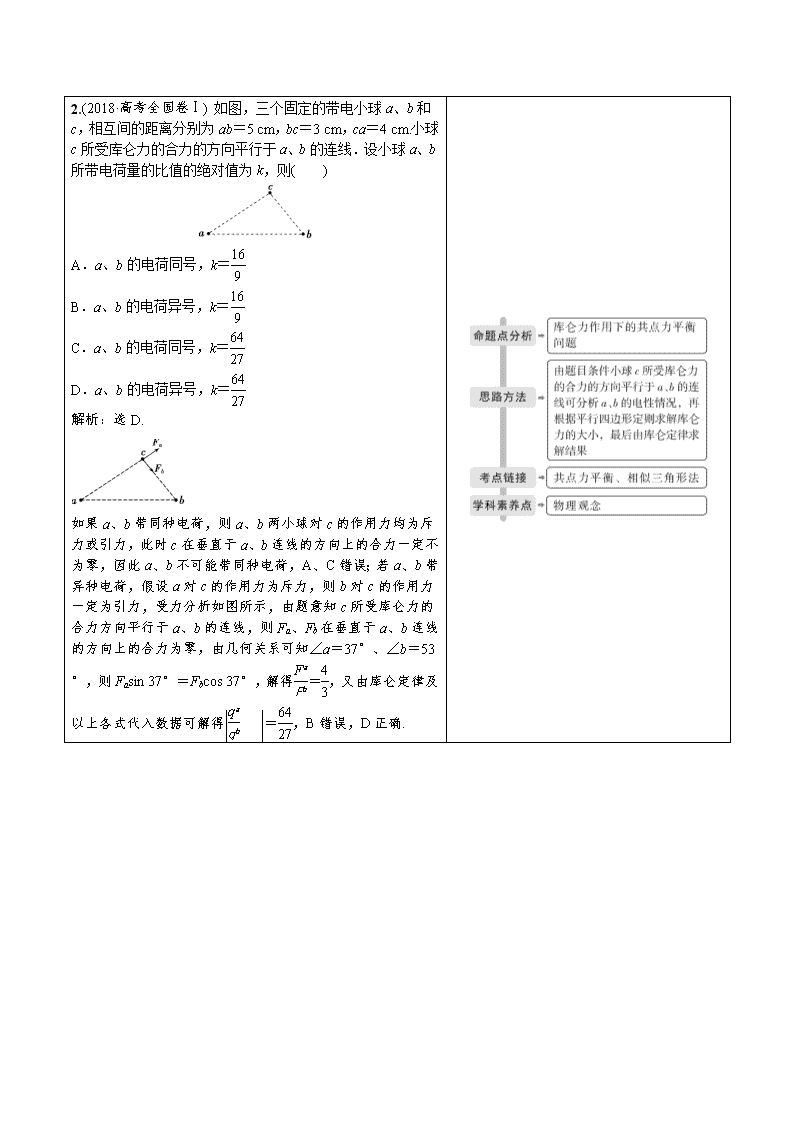
第1讲　力与物体的平衡 真题再现 考情分析 ‎1．(多选)(2019·高考全国卷Ⅰ)如图，一粗糙斜面固定在地面上，斜面顶端装有一光滑定滑轮．一细绳跨过滑轮，其一端悬挂物块N.另一端与斜面上的物块M相连，系统处于静止状态．现用水平向左的拉力缓慢拉动N，直至悬挂N的细绳与竖直方向成45°.已知M始终保持静止，则在此过程中(　　)‎ A．水平拉力的大小可能保持不变 B．M所受细绳的拉力大小一定一直增加 C．M所受斜面的摩擦力大小一定一直增加 D．M所受斜面的摩擦力大小可能先减小后增加 解析：选BD. 对N进行受力分析如图所示，因为N的重力与水平拉力F的合力和细绳的拉力T是一对平衡力，从图中可以看出水平拉力的大小逐渐增大，细绳的拉力也一直增大，选项A错误，B正确；M的质量与N的质量的大小关系不确定，设斜面倾角为θ，若mNg≥mMgsin θ，则M所受斜面的摩擦力大小会一直增大，若mNgm2，如图所示，若三角形木块和两物体 都是静止的，则粗糙水平面对三角形木块(　　)‎ A．有摩擦力的作用，摩擦力的方向水平向右 B．有摩擦力的作用，摩擦力的方向水平向左 C．有摩擦力的作用，但摩擦力的方向不能确定，因m1、m2、θ1、θ2的数值均未给出 D．以上结论都不对 解析：选D.法一(隔离法)：把三角形木块隔离出来，它的两个斜面上分别受到两物体对它的压力 FN1、FN2，摩擦力 F1、F2.由两物体的平衡条件知，这四个力的大小分别为 FN1＝m1gcos θ1，FN2＝m2gcos θ2‎ F1＝m1gsin θ1，F2＝m2gsin θ2‎ 它们的水平分力的大小(如图所示)分别为 FN1x＝FN1sin θ1＝m1gcos θ1sin θ1‎ FN2x＝FN2sin θ2＝m2gcos θ2sin θ2‎ F1x＝F1cos θ1＝m1gcos θ1sin θ1‎ F2x＝F2cos θ2＝m2gcos θ2sin θ2‎ 其中 FN1x＝F1x，FN2x＝F2x，即它们的水平分力互相平衡，木块在水平方向无滑动趋势，因此不受水平面的摩擦力作用．‎ 法二(整体法)：‎ 由于三角形木块和斜面上的两物体都静止，可以把它们看成一个整体，受力如图所示．设三角形木块质量为 M，则竖直方向受到重力(m1＋m2＋M)g和支持力 FN作用处于平衡状态，水平方向无任何滑动趋 势，因此不受水平面的摩擦力作用．‎ ‎2．(2019·高考全国卷Ⅱ)物块在轻绳的拉动下沿倾角为30°的固定斜面向上匀速运动，轻绳与斜面平行．已知物块与斜面之间的动摩擦因数为，重力加速度取10 m/s2.若轻绳能承受的最大张力为1 500 N，则物块的质量最大为(　　)‎ A．150 kg B．100 kg C．200 kg D．200 kg 解析：选A.设物块的质量最大为m，将物块的重力沿斜面方向和垂直斜面方向分解，由平衡条件，在沿斜面方向有F＝mgsin 30°＋μmgcos 30°，解得m＝150 kg，A项正确．‎ ‎3．(2019·烟台联考) 如图所示，在固定斜面上的一物块受到一外力 F 的作用，F 平行于斜面向上．若要物块在斜面上保持静止，F 的取值应有一定范围，‎ 已知其最大值和最小值分别为 F1和 F2(F2>0)．由此可求出(　　)‎ A．物块的质量 B．斜面的倾角 C．物块与斜面间的最大静摩擦力 D．物块对斜面的正压力 解析：选C.设斜面倾角为θ，斜面对物块的最大静摩擦力为 Ff，当 F 取最大值 F1时，最大静摩擦力 Ff沿斜面向下，由平衡条件得 F1＝mgsin θ＋Ff；当 F 取最小值 F2时，Ff沿斜面向上，由平衡条件得 F2＝mgsin θ－Ff，联立两式可求出最大静摩擦力Ff＝，选项 C 正确．FN＝mgcos θ，F1＋F2＝2mgsin θ，所以不能求出物块的质量、斜面的倾角和物块对斜面的正压力．‎ ‎4．(2017·高考全国卷Ⅲ)一根轻质弹性绳的两端分别固定在水平天花板上相距80 cm 的两点上，弹性绳的原长也为80 cm.将一钩码挂在弹性绳的中点，平衡时弹性绳的总长度为100 cm；再将弹性绳的两端缓慢移至天花板上的同一点，则弹性绳的总长度变为(弹性绳的伸长始终处于弹性限度内)(　　)‎ A．86 cm B．92 cm C．98 cm D．104 cm 解析：选B.将钩码挂在弹性绳的中点时，由数学知识可知钩码两侧的弹性绳(劲度系数设为k)与竖直方向夹角θ均满足sin θ＝，对钩码(设其重力为G)静止时受力分析，得G＝2kcos θ；弹性绳的两端移至天花板上的同一点时，对钩码受力分析，得G＝2k，联立解得L＝92 cm，可知A、C、D项错误，B项正确．‎ ‎5. 如图，两个轻环a和b套在位于竖直面内的一段固定圆弧上；一细线穿过两轻环，其两端各系一质量为m的小球．在a和b之间的细线上悬挂一小物块．平衡时，a、b间的距离恰好等于圆弧的半径．不计所有摩擦．小物块的质量为(　　)‎ A． B．m C．m D．2m 解析：选C.由于轻环不计重力，故细线对轻环的拉力的合力与圆弧对轻环的支持力等大反向，即沿半径方向；又两侧细线对轻环拉力相等，故轻环所在位置对应的圆弧半径为两细线的角平分线，因为两轻环间的距离等于圆弧的半径，故两轻环与圆弧圆心构成等边三角形；又小球对细线的拉力方向竖直向下，由几何知识可知，两轻环间的细线夹角为120°，对小物块进行受力分析，由三力平衡知识可知，小物块质量与小球质量相等，均为m，C项正确．‎ ‎6．(2017·高考全国卷Ⅱ) 如图，一物块在水平拉力F 的作用下沿水平桌面做匀速直线运动．若保持F的大小不变，而方向与水平面成60°角，物块也恰好做匀速直线运动．物块与桌面间的动摩擦因数为(　　)‎ A．2－ B． C． D． ‎ 解析：选C.当拉力水平时，物块做匀速运动，则F＝μmg，当拉力方向与水平方向的夹角为60°时，物块也刚好做匀速运动，则Fcos 60°＝μ(mg－Fsin 60°)，联立解得μ＝，A、B、D项错误，C项正确．‎ ‎7．如图所示，匀强电场的电场强度方向与水平方向夹角为30°且斜向右上方，匀强磁场的方向垂直于纸面(图中未画出)．一质量为m、电荷量为q的带电小球(可视为质点)以与水平方向成30°角斜向左上方的速度v做匀速直线运动，重力加速度为g，则(　　)‎ A．匀强磁场的方向可能垂直于纸面向外 B．小球一定带正电荷 C．电场强度大小为 D．磁感应强度的大小为 解析：选C.小球做匀速直线运动，受到的合力为零，假设小球带正电，则小球的受力情况如图甲所示，小球受到的洛伦兹力沿虚线但方向未知，小球受到的重力与电场力的合力与洛伦兹力不可能平衡，故小球不可能做匀速直线运动，假设不成立，小球一定带负电，选项B错误；小球的受力情况如图乙所示，小球受到的洛伦兹力一定斜向右上方，根据左手定则，匀强磁场的方向一定垂直于纸面向里，选项A错误；根据几何关系，电场力大小qE＝mg，洛伦兹力大小qvB＝mg，解得E＝，B＝，选项C正确，D错误．‎ ‎8．(2019·青岛模拟) 质量为m的四只完全相同的足球叠成两层放在水平面上，底层三只足球刚好接触成三角形，上层一只足球放在底层三只足球的正上面，系统保持静止．若最大静摩擦力等于滑动摩擦力，则(　　)‎ A．底层每个足球对地面的压力为mg B．底层每个足球之间的弹力为零 C．下层每个足球对上层足球的支持力大小为 D．足球与水平面间的动摩擦因数至少为 解析：选B. 根据整体法，设下面每个球对地面的压力均为FN，则3FN＝4mg，故FN＝mg，A错误；四个球的球心连线构成了正四面体，下层每个足球之间的弹力为零，B正确；上层足球受到重力、下层足球对上层足球的三个支持力，由于三个支持力的方向不是竖直向上，所以三个支持力在竖直方向的分量之和等于重力，则下层每个足球对上层足球的支持力大小大于，C错误；根据正四面体几何关系可求，F与mg夹角的余弦值cos θ＝，正弦值sin θ＝，则有F·＋mg＝FN＝mg，F＝Ff，解得Ff＝mg，F＝mg，则μ≥＝，所以足球与水平面间的动摩擦因数至少为，故D错误．‎ ‎9. (2019·济宁二模)三段细绳OA、OB、OC结于O点，另一端分别系于竖直墙壁、水平顶壁和悬挂小球，稳定后OA呈水平状态．现保持O点位置不变，缓慢上移 A点至D点的过程中，关于OA绳上的拉力变化情况的判断正确的是(　　)‎ A．一直增大 B．一直减小 C．先增大后减小 D．先减小后增大 解析：选D.可运用动态图解法，由图可知，当 OA 与 OB 垂直时，OA 上的拉力最小，故 D 正确．‎ ‎10．(2019·长沙模拟) 如图所示，固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔．质量为m的小球套在圆环上，一根细线的下端系着小球，上端穿过小孔用手拉住．现拉动细线，使小球沿圆环缓慢上移，在移动过程中手对线的拉力F和环对小球的弹力FN的大小变化情况是(　　)‎ A．F减小，FN不变 B．F不变，FN减小 C．F不变，FN增大 D．F增大，FN减小 解析：选A.对小球受力分析，其所受的三个力组成一个闭合三角形，如图所示，力三角形与圆内的三角形相似，由几何关系可知＝＝，小球缓慢上移时mg不变，R不变，L减小，故F减小，FN大小不变，A正确．‎ 二、多项选择题 ‎11. (2018·高考天津卷)明朝谢肇淛的《五杂组》中记载：“明姑苏虎丘寺塔倾侧，议欲正之，非万缗不可．一游僧见之曰：无烦也，我能正之．”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去，经月余扶正了塔身．假设所用的木楔为等腰三角形，木楔的顶角为θ，现在木楔背上加一力F，方向如图所示，木楔两侧产生推力FN，则(　　)‎ A．若F一定，θ大时FN大 B．若F一定，θ小时FN大 C．若θ一定，F大时FN大 D．若θ一定，F小时FN大 解析：选BC.木楔两侧面产生的推力合力大小等于F，由力的平行四边形定则可知，FN＝，由表达式可知，若F一定，θ越小，FN越大，A项错误，B项正确；若θ一定，F越大，FN越大，C项正确，D项错误．‎ ‎12．如图所示，轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点，‎ 悬挂衣服的衣架挂钩是光滑的，挂于绳上处于静止状态．如果只人为改变一个条件，当衣架静止时，下列说法正确的是(　　)‎ A．绳的右端上移到b′，绳子拉力不变 B．将杆N向右移一些，绳子拉力变大 C．绳的两端高度差越小，绳子拉力越小 D．若换挂质量更大的衣服，则衣架悬挂点右移 解析：选AB.设两段绳子间的夹角为2α，绳子的拉力大小为F，由平衡条件可知，2Fcos α＝mg，所以F＝，设绳子总长为L，两杆间距离为s，由几何关系L1sin α＋L2sin α＝s，得sin α＝＝，绳子右端上移，L、s都不变，α不变，绳子张力F也不变，A正确；杆N向右移动一些，s变大，α变大，cos α变小，F变大，B正确；绳子两端高度差变化，不影响s和L，所以F不变，C错误；衣服质量增加，绳子上的拉力增加，由于α不会变化，悬挂点不会右移，D错误．‎ ‎13．(2019·德州模拟)如图所示，重物A被绕过小滑轮P的细线所悬挂，小滑轮P被一根细线系于天花板上的O点，B物体放在粗糙的水平桌面上，O′是三根线的结点，bO′水平拉着B物体，cO′竖直拉着重物 C，aO′、bO′与cO′的夹角如图所示．细线、小滑轮的重力和细线与滑轮间的摩擦力均可忽略，整个装置处于静止状态．若悬挂小滑轮的细线 OP 的张力大小是20 N，则下列说法中正确的是(g＝10 m/s2)(　　)‎ A．重物 A 的质量为2 kg B．桌面对 B 物体的摩擦力大小为 10 N C．重物 C 的质量为1 kg D．OP 与竖直方向的夹角为60°‎ 解析：选ABC.以小滑轮 P 为研究对象，受力分析如图甲所示，则有2Tcos 30°＝F，故T＝＝20 N，由于T＝mAg，故mA＝2 kg，则选项A正确；以 O′点为研究对象，受力分析如图乙所示，由平衡条件得：Tcos 30°＝Fb，Fb＝10 N，Tsin 30°＝FC＝mCg，故 mC＝1 kg，则选项C正确；又因为 Fb＝－f，所以选项 B 正确；OP 与竖直方向的夹角应为30°，所以选项 D 错误．‎ ‎14. 表面光滑、半径为R的半球固定在水平地面上，球心O的正上方O′处有一无摩擦定滑轮，轻质细绳两端各系一个可视为质点的小球挂在定滑轮上，如图所示．两小球平衡时，若滑轮两侧细绳的长度分别为L1＝2.4R和L2＝2.5R，则这两个小球的质量之比为，小球与半球之间的压力之比为，则以下说法正确的是(　　)‎ A．＝ B．＝ C．＝ D．＝ 解析：选BC.先以左侧小球为研究对象，分析受力情况：重力m1g、绳子的拉力FT和半球的支持力FN1，作出受力分析图．‎ 由平衡条件得知，拉力FT和支持力FN的合力与重力m1g大小相等、方向相反．设OO′＝h，根据三角形相似得＝＝，解得m1g＝，FN1＝…①同理，以右侧小球为研究对象，得：m2g＝，FN2＝…②，由①∶②得＝＝，＝＝.‎ ‎15. (2019·滨州质检)如图所示，在竖直平面内，一根不可伸长的轻质软绳两端打结系于“V”形杆上的A、B两点，已知OM边竖直，且|AO|＝|OB|，细绳绕过光滑的滑轮，重物悬挂于滑轮下处于静止状态．若在纸面内绕端点O按顺时针方向缓慢转动“V”形杆，直到ON边竖直，绳子的张力为T，A点处绳子与杆之间摩擦力大小为F，则(　　)‎ A．张力T一直增大 B．张力T先增大后减小 C．摩擦力F一直减小 D．摩擦力F先增大后减小 解析：选BC.设滑轮两侧绳子与竖直方向的夹角α，受力如图甲，在纸面内绕端点O按顺时针方向缓慢转动“V”形杆，直到ON边竖直，AB的长度不变，AB在水平方向的投影先变长后变短，绳子与竖直方向的夹角α先变大后变小，所以张力T＝先增大后减小，故A错误，B正确；以A点为研究对象，受力分析如图乙．根据平衡 条件可知，F＝Tcos(α＋β)＝＝(cos β－tan αsin β)，在纸面内绕端点O按顺时针方向缓慢转动“V”形杆，绳子与竖直方向的夹角α先变大后变小，OA杆与竖直方向的夹角β一直变大，当绳子与竖直方向的夹角α变大时，摩擦力减小，当绳子与竖直方向的夹角α变小时，但(α＋β)还是在增大，所以摩擦力还是在减小，故C正确，D错误．‎