人教版高中物理一轮复习课件：小专题复习课(5)

人教版高中物理一轮复习课件：小专题复习课(5)

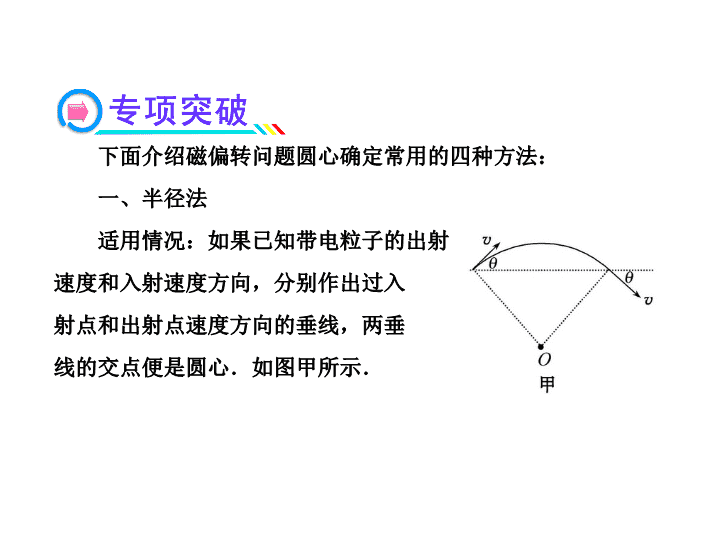
（五） 磁偏转问题圆心确定四法 带电粒子(不计重力)垂直射入匀强磁场，粒子的运动 轨迹是圆周或圆弧．这类问题是常见的典型的力学、磁场知识 结合的综合题，在高考中多次考查，是考试的难点． 求解这类问题的关键是：定圆心画出轨迹,求出半径,确定 圆心角等．其中解决带电粒子在有界磁场中的运动、确定圆心 是解题的难点． 下面介绍磁偏转问题圆心确定常用的四种方法： 一、半径法 适用情况：如果已知带电粒子的出射 速度和入射速度方向，分别作出过入 射点和出射点速度方向的垂线，两垂 线的交点便是圆心．如图甲所示． 【典例1】电视机的显像管中，电子束的 偏转是使用磁偏转技术实现的．电子束 经过电压为U的加速电场后，进入一圆形 匀强磁场区，如图所示，磁场方向垂直 于圆面．磁场区的中心为O，半径为r．当不加磁场时，电子束 将通过O点而达到屏幕的中心M点．为了让电子束射到屏幕边缘 P，需要加磁场，使电子束偏转一已知角度θ，此时磁场的磁感 应强度为多大？(已知电子质量为m，电荷量为e) 【深度剖析】分别作入射点和出射点速度方向的垂线，其交点 为电子做匀速圆周运动的圆心C，以v表示电子进入磁场时的速 度，则 ① ② 又有 ③ 由以上各式解得： 21eU mv2  2mvevB R  rtan 2 R   1 2mUB tanr e 2  二、角平分线法 适用情况：如果已知带电粒子的出射 速度和入射速度方向，则入射速度方 向的延长线和出射速度方向的反向延 长线夹角的角平分线与入射速度垂线 的交点就是圆心.如图乙所示. 【典例2】一质量为m、带电量为q的粒子，以速度v0从O点沿y 轴正方向射入磁感应强度为B的一圆形匀强磁场区域，磁场方 向垂直于纸面，粒子飞出磁场区域后，从b处穿过x轴，速度方 向与x轴正方向夹角为30°，不计重力．求： (1)圆形磁场区域的最小面积； (2)粒子从O点进入磁场区域到达b点所经历的时间及b点坐标． 【深度剖析】(1)由于粒子沿y轴正方 向射入，所以圆心必在x轴上，反向 延长b处的速度方向与y轴相交于C点， 作∠OCA的角平分线与x轴相交于O′ 点，过O′点作bC的垂线，垂足为A点．则O′A=O′O=R,所以， 以OA为直径的圆的磁场区域面积最小．设圆形磁场区域的半径为 r．由牛顿第二定律得： 由几何关系得： 2 0 0 mvqv B R  3r R2  2 2 2 0 min 2 2 3 m vS r 4B q    (2)粒子从O点沿圆弧到A点，所经历的时间 sAb=Rcot30° OA T 2 mt 3 3qB   Ab Ab 0 s 3mt v Bq   所以粒子从O点进入磁场区域到达b点所经历的时间为 b点横坐标为 ,故b点坐标为( ) OA Ab m 2t t t ( 3 )Bq 3     O b Rs 2Rsin30   0 b 3mvx R 2R Bq    03mv ,0Bq 三、垂直平分线法 适用情况：如果已知带电粒子的入射速度方向和做圆周 运动轨迹的一条弦，先作出过入射点速度方向的垂线，然后 作弦的垂直平分线，两垂线的交点便是圆心． 【典例3】如图,虚线MN是一垂直纸面的平面与纸 面的交线，在平面右侧的空间存在磁感应强度为 B的匀强磁场，方向垂直纸面向外，O是MN上的一 点，从O点可以向磁场区域发射电荷量为+q、质量 为m、速率为v的粒子，粒子射入磁场时的速度可在纸面内各个 方向．已知先后射入的两个粒子恰好在磁场中给定的P点相遇， P到O点的距离为L，不计重力及粒子间的相互作用． (1)求所考查的粒子在磁场中运动的轨道半径; (2)求这两个粒子从O点射入磁场时的时间间隔. 【深度剖析】(1)设粒子在磁场中做圆周运动的轨道半径为R， 洛伦兹力充当向心力，由牛顿第二定律，有 解得： 2mvqvB R  mvR Bq  (2)如图所示，为两粒子在匀强磁场中运动的轨迹图． 作图方法是：作OP的垂直平分线，分别过入 射点O作入射速度1、2的垂线．两垂线与垂 直平分线的交点分别为O1、O2，则O1、O2为 圆心，粒子1转过的角度为∠OO1P=π+θ， 粒子2转过的角度为∠OO2P=π-θ 两粒子在磁场中运动的周期均为 2 mT qB  粒子1从O点运动到P点所用的时间为： 粒子2从O点运动到P点所用的时间为： 两粒子射入的时间间隔：Δt=t1-t2= 又因为：∠O1OP= ，故 1t T2     2t T2     T  2  Lcos 2 2R   1 2 4m qBLt t t arccosqB 2mv     四、直角直径法 适用情况：如果已知带电粒子的入 射速度方向和过入射点的一条弦，先作 出过入射点速度方向的垂线，然后过弦 的另一端点作弦的垂线，两垂线的交点 和入射点的连线便是该圆的直径，作直 径的中点便是圆心． 【典例4】在直角坐标系xOy中，有一半径为R的圆形匀强磁场区 域，磁感应强度为B，磁场方向垂直xOy平面指向纸面内，该区 域的圆心坐标为(R,0)，有一个质量为m，带电量为-q的粒子， 由静止经电场加速后从点( )沿x轴正方向射入磁场，粒子从 射入到射出磁场通过了该磁场的最大距离，不计重力影响．试 求： (1)粒子在磁场区域经历的时间; (2)加速电场的电压. R0 2， 【深度剖析】(1)因为粒子从射入到射出 磁场通过了该磁场的最大距离，即MP应 是圆形磁场区域的直径，同时也是粒子 做圆周运动的一条弦．过P点作直线 NP⊥MP,与竖直线交于N点．作MN的中点 即是粒子做圆周运动的圆心(直角直径法)．设从M点射入磁场的 速度方向与半径MC夹角为θ，故 ，即θ=30°R 12sin R 2    在磁场中偏转的角度为α=2θ=60°,有 带电粒子在磁场中运动的周期为 所以粒子在磁场区域经历的时间 t T2   2 mT Bq  mt 3Bq  (2)设粒子在磁场中做圆周运动的半径为r,由洛伦兹力提供向心 力得： ① r=2R ② 带电粒子在加速电场加速过程中，由功能关系得： ③ 联立以上各式解得： 2mvqvB = r 21qU mv2  2 22B R qU m  以上四种方法是确定圆心极为有效的办法，在解题过程中要灵 活选择使用，突破圆心的确定这一难点，就会使此类问题变得 迎刃而解． 在真空中,半径为r=3×10-2 m的圆形 区域内,有一匀强磁场,磁场的磁感应 强度为B=0.2 T,方向如图所示,一带 正电粒子,以初速度v0=106 m/s的速度 从磁场边界上直径ab一端a点处射入磁 场,已知该粒子荷质比为q/m=108 C/kg,不计粒子重力,则: (1)粒子在磁场中做匀速圆周运动的半径是多少? (2)若要使粒子飞离磁场时有最大的偏转角,其入射时粒子的方 向应如何?最大偏转角多大? 【解析】(1)设粒子做圆周运动的半径为R,则 得 2 0 0 vqv B m R  ， 0mvR 0.05 mBq   (2)由分析知,弦ab是粒子轨迹上的弦, 也是圆形磁场的弦,如图所示.粒子在 磁场中运动的最长弦就是ab,其对应的 圆心角就是最大的偏转角α,此时初速 度方向与ab连线夹角为θ,则 .2 ＝ 由几何知识有 得α=74° 所以 故粒子以与ab夹角为37°斜向右上方入射时,粒子飞离磁场时有 最大偏转角,其最大值为74°. 答案:(1)0.05 m (2)见解析 r 3sin 2 R 5    372    