- 2021-05-26 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【物理】2019届二轮复习力的合成与分解学案(全国通用)
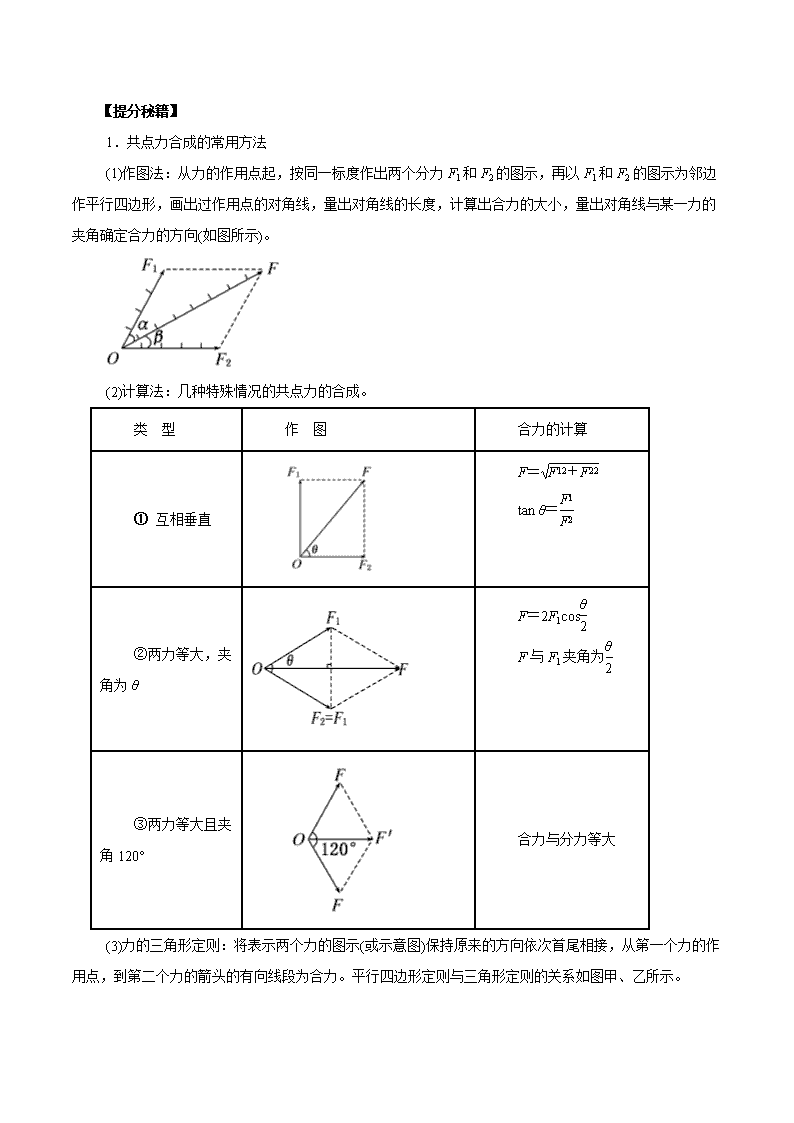
2019届二轮复习 力的合成与分解 学案(全国通用) 1.会用平行四边形定则、三角形定则进行力的合成与分解. 2.会用正交分解法进行力的合成与分解. 热点题型一 力的合成问题 例1、一物体受到三个共面共点力F1、F2、F3的作用,三力的矢量关系如图所示(小方格边长相等),则下列说法正确的是 ( ) A.三力的合力有最大值F1+F2+F3,方向不确定 B.三力的合力有唯一值3F3,方向与F3同向 C.三力的合力有唯一值2F3,方向与F3同向 D.由题给条件无法求合力大小 答案:B 【提分秘籍】 1.共点力合成的常用方法 (1)作图法:从力的作用点起,按同一标度作出两个分力F1和F2的图示,再以F1和F2的图示为邻边作平行四边形,画出过作用点的对角线,量出对角线的长度,计算出合力的大小,量出对角线与某一力的夹角确定合力的方向(如图所示)。 (2)计算法:几种特殊情况的共点力的合成。 类 型 作 图 合力的计算 ① 互相垂直 F= tan θ= ②两力等大,夹角为θ F=2F1cos F与F1夹角为 ③两力等大且夹角120° 合力与分力等大 (3)力的三角形定则:将表示两个力的图示(或示意图)保持原来的方向依次首尾相接,从第一个力的作用点,到第二个力的箭头的有向线段为合力。平行四边形定则与三角形定则的关系如图甲、乙所示。 2.合力的大小范围 (1)两个共点力的合成 |F1-F2|≤F合≤F1+F2 即两个力大小不变时,其合力随夹角的增大而减小,当两力反向时,合力最小,为|F1-F2|,当两力同向时,合力最大,为F1+F2。 (2)三个共点力的合成 ①三个力共线且同向时,其合力最大,为F1+F2+F3。 ②任取两个力,求出其合力的范围,如果第三个力在这个范围之内,则三个力的合力最小值为零;如果第三个力不在这个范围内,则合力最小值等于最大的力减去另外两个力。 绳构成的正方形,点O、a、b、c等为网绳的结点。当网水平张紧时,若质量为m的运动员从高处竖直落下,并恰好落在O点,当该处下凹至最低点时,网绳aOe、cOg均成120°向上的张角,此时O点受到的向下的冲击力为F,则这时O点周围每根网绳的拉力的大小为( ) A. B. C. D. 解析:设每根网绳的拉力大小为F′,对结点O有: 4F′cos 60°-F=0,解得F′=,选项B正确。 答案:B 热点题型四 绳上的“死结”和“活结”模型 例4、如图甲所示,细绳AD跨过固定的水平轻杆BC右端的定滑轮挂住一个质量为M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量为M2的物体,求: (1)细绳AC段的张力FTAC与细绳EG的张力FTEG之比; (2)轻杆BC对C端的支持力; (3)轻杆HG对G端的支持力。 (1)图甲中细绳AD跨过定滑轮拉住质量为M1的物体,物体处于平衡状态,细绳AC段的拉力FTAC=FTCD=M1g 图乙中由FTEGsin 30°=M2g,得FTEG=2M2g。 所以=。 (2)图甲中,三个力之间的夹角都为120°,根据平衡规律有FNC=FTAC=M1g,方向与水平方向成30°,指向右上方。 [方法规律] (1)对轻质杆,若与墙壁通过转轴相连,则杆产生的弹力方向一定沿杆。 (2)若轻质杆一端固定,则杆产生的弹力有可能沿杆,也有可能不沿杆,杆的弹力方向,可根据共点力的平衡求得。 (3)“死结”分开的两段绳子上的弹力不一定相等,“活结”分开的两段绳子上的弹力大小一定相等,“活结”分开的两段绳子合力的方向一定沿这两段绳子夹角的平分线。 查看更多