【物理】2020届二轮复习专题三第9讲磁场及其对电流的作用 带电粒子在磁场中的运动学案
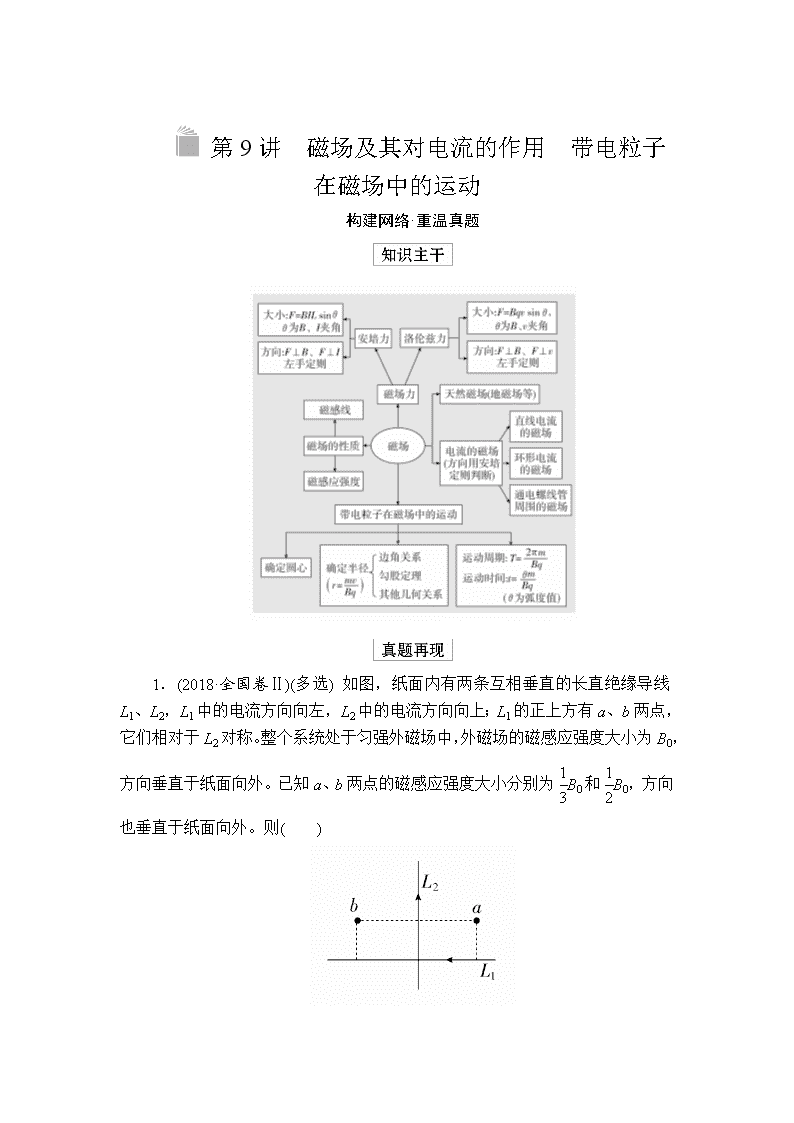
第9讲 磁场及其对电流的作用 带电粒子在磁场中的运动
构建网络·重温真题
1.(2018·全国卷Ⅱ)(多选) 如图,纸面内有两条互相垂直的长直绝缘导线L1、L2,L1中的电流方向向左,L2中的电流方向向上;L1的正上方有a、b两点,它们相对于L2对称。整个系统处于匀强外磁场中,外磁场的磁感应强度大小为B0,方向垂直于纸面向外。已知a、b两点的磁感应强度大小分别为B0和B0,方向也垂直于纸面向外。则( )
A.流经L1的电流在b点产生的磁感应强度大小为B0
B.流经L1的电流在a点产生的磁感应强度大小为B0
C.流经L2的电流在b点产生的磁感应强度大小为B0
D.流经L2的电流在a点产生的磁感应强度大小为B0
答案 AC
解析 L1在a、b两点产生的磁场磁感应强度大小相等,设为B1,方向都垂直于纸面向里,而L2在a点产生的磁场磁感应强度大小设为B2,方向垂直纸面向里,在b点产生的磁场磁感应强度大小也为B2,方向垂直纸面向外,规定向外为正方向,根据矢量叠加原理可知B0-B1-B2=B0,B2+B0-B1=B0,联立这两式可解得:B1=B0,B2=B0,故A、C正确。
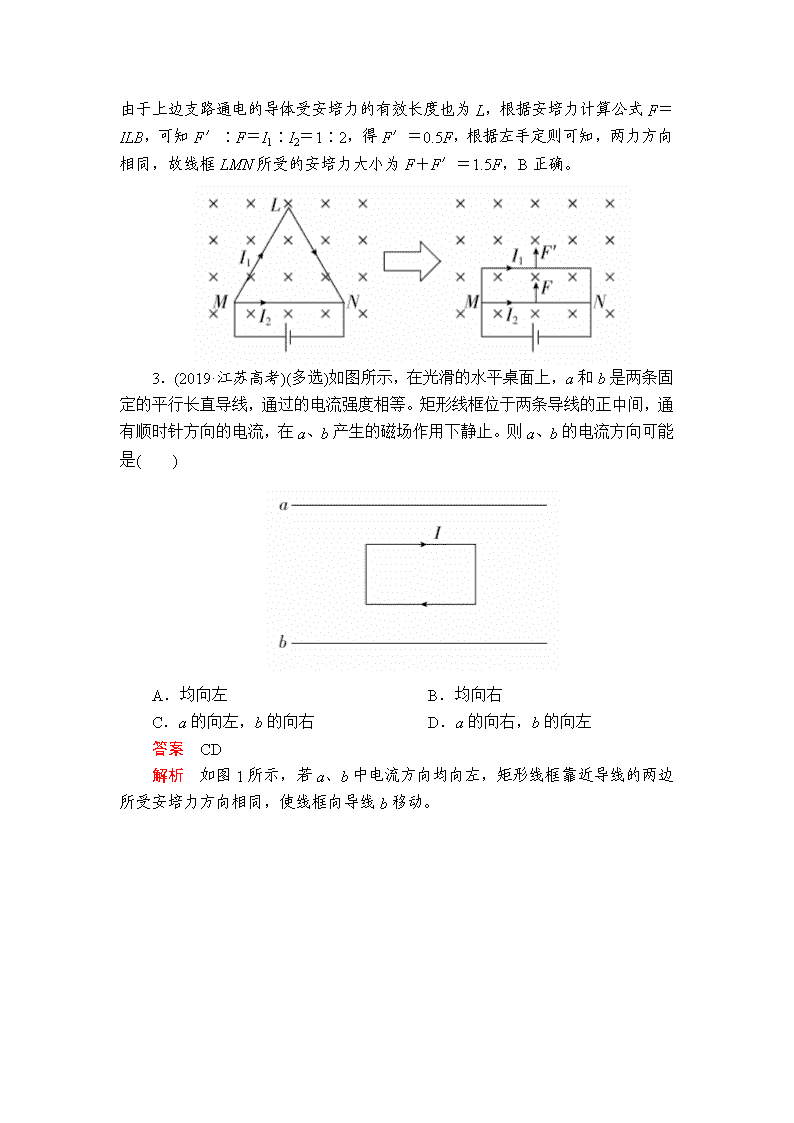
2.(2019·全国卷Ⅰ) 如图,等边三角形线框LMN由三根相同的导体棒连接而成,固定于匀强磁场中,线框平面与磁感应强度方向垂直,线框顶点M、N与直流电源两端相接。已知导体棒MN受到的安培力大小为F,则线框LMN受到的安培力的大小为( )
A.2F B.1.5F C.0.5F D.0
答案 B
解析 设每根导体棒的电阻为R,长度为L,则电路中,上下两支路电阻之比为R1∶R2=2R∶R=2∶1,上下两支路电流之比为I1∶I2=1∶2。如图所示,由于上边支路通电的导体受安培力的有效长度也为L,根据安培力计算公式F=ILB,可知F′∶F=I1∶I2=1∶2,得F′=0.5F,根据左手定则可知,两力方向相同,故线框LMN所受的安培力大小为F+F′=1.5F,B正确。
3.(2019·江苏高考)(多选)如图所示,在光滑的水平桌面上,a和b是两条固定的平行长直导线,通过的电流强度相等。矩形线框位于两条导线的正中间,通有顺时针方向的电流,在a、b产生的磁场作用下静止。则a、b的电流方向可能是( )
A.均向左 B.均向右
C.a的向左,b的向右 D.a的向右,b的向左
答案 CD
解析 如图1所示,若a、b中电流方向均向左,矩形线框靠近导线的两边所受安培力方向相同,使线框向导线b移动。
同理可知,若a、b中电流均向右,线框向导线a移动,故A、B不符合题意。
若a导线的电流方向向左,b导线的电流方向向右,a、b中电流I′在线框所在处产生的磁场方向如图2所示,线框靠近导线的两边所在处的磁感应强度相同,所受的安培力大小相等、方向相反,线框静止。
同理可知,若a导线的电流方向向右,b导线的电流方向向左,线框也静止,C、D符合题意,故选C、D。
4.(2017·全国卷Ⅰ) (多选)如图,三根相互平行的固定长直导线L1、L2和L3两两等距,均通有电流I,L1中电流方向与L2中的相同,与L3中的相反。下列说法正确的是( )
A.L1所受磁场作用力的方向与L2、L3所在平面垂直
B.L3所受磁场作用力的方向与L1、L2所在平面垂直
C.L1、L2和L3单位长度所受的磁场作用力大小之比为1∶1∶
D.L1、L2和L3单位长度所受的磁场作用力大小之比为 ∶∶1
答案 BC
解析 如图,由磁场的叠加知,L2与L3中的电流在L1处产生的合磁场的方向在L2、L3连线的中垂线上,由左手定则知,L1所受磁场作用力的方向与L2、L3所在平面平行,A错误。L1与L2中的电流在L3处产生的合磁场的方向与L1、L2的连线平行,由左手定则知,L3所受磁场作用力的方向与L1、L2所在平面垂直,B正确。由几何关系知,设电流在另外导线处产生磁场的磁感应强度为B,而L1、L2所在处两个磁场方向的夹角均为120°,则B合=B,而L3
所在处两个磁场方向的夹角为60°,则B′合=B,由F=ILB知,L1、L2和L3单位长度所受的磁场作用力大小之比为1∶1∶,C正确,D错误。
5.(2017·全国卷Ⅱ)(多选)某同学自制的简易电动机示意图如图所示。矩形线圈由一根漆包线绕制而成,漆包线的两端分别从线圈的一组对边的中间位置引出,并作为线圈的转轴。将线圈架在两个金属支架之间,线圈平面位于竖直面内,永磁铁置于线圈下方。为了使电池与两金属支架连接后线圈能连续转动起来,该同学应将( )
A.左、右转轴下侧的绝缘漆都刮掉
B.左、右转轴上下两侧的绝缘漆都刮掉
C.左转轴上侧的绝缘漆刮掉,右转轴下侧的绝缘漆刮掉
D.左转轴上下两侧的绝缘漆都刮掉,右转轴下侧的绝缘漆刮掉
答案 AD
解析 装置平面示意图如图所示。如图所示的状态,磁感线方向向上,若形成通路,线圈下边导线中电流方向向左,受垂直纸面向里的安培力,同理,上边导线中电流受安培力垂直纸面向外,使线圈转动。当线圈上边导线转到下边时,若仍通路,线圈上、下边中电流方向与图示方向相比均反向,受安培力反向,阻碍线圈转动。若要线圈连续转动,要求左、右转轴只能上一侧或下一侧形成通路,另一侧断路。故选A、D。
6.(2019·全国卷Ⅱ) 如图,边长为l的正方形abcd内存在匀强磁场,磁感应强度大小为B,方向垂直于纸面(abcd所在平面)向外。ab边中点有一电子发射源O,可向磁场内沿垂直于ab边的方向发射电子。已知电子的比荷为k。则从a、d两点射出的电子的速度大小分别为( )
A.kBl,kBl B.kBl,kBl
C.kBl,kBl D.kBl,kBl
答案 B
解析 若电子从a点射出,运动轨迹如图线①,有
qvaB=m,Ra=
解得va===;
若电子从d点射出,运动轨迹如图线②,
有qvdB=m
R=2+l2
解得vd===。B正确。
7.(2017·全国卷Ⅱ) 如图,虚线所示的圆形区域内存在一垂直于纸面的匀强磁场,P为磁场边界上的一点。大量相同的带电粒子以相同的速率经过P点,在纸面内沿不同方向射入磁场。若粒子射入速率为v1,这些粒子在磁场边界的出射点分布在六分之一圆周上;若粒子射入速率为v2,相应的出射点分布在三分之一圆周上。不计重力及带电粒子之间的相互作用。则v2∶v1为( )
A.∶2 B.∶1 C.∶1 D.3∶
答案 C
解析 相同的带电粒子垂直匀强磁场入射均做匀速圆周运动。粒子以v1入射,一端为入射点P,对应圆心角为60°(对应六分之一圆周)的弦PP′必为垂直该弦入射粒子运动轨迹的直径2r1,如图甲所示,设圆形区域的半径为R,由几何关系知r1=R。其他不同方向以v1入射的粒子的出射点在PP′对应的圆弧内。
同理可知,粒子以v2入射及出射情况如图乙所示。由几何关系知r2=
=R,可得r2∶r1=∶1。因为m、q、B均相同,由公式r=可得v∝r,所以v2∶v1=∶1。故选C。
8.(2019·江苏高考)如图所示,匀强磁场的磁感应强度大小为B。磁场中的水平绝缘薄板与磁场的左、右边界分别垂直相交于M、N,MN=L,粒子打到板上时会被反弹(碰撞时间极短),反弹前后水平分速度不变,竖直分速度大小不变、方向相反。质量为m、电荷量为-q的粒子速度一定,可以从左边界的不同位置水平射入磁场,在磁场中做圆周运动的半径为d,且d
45°,粒子做圆周运动的周期:T=,则粒子在磁场中运动的最短时间tmin=T>,最长时间tmax=T=,故C错误,D正确。
[答案] AD
处理带电粒子在有界磁场中运动问题的方法技巧
(1)解答有关运动电荷在有界匀强磁场中的运动问题时,我们可以先将有界磁场视为无界磁场,假设粒子能够做完整的圆周运动,确定粒子做圆周运动的圆心,作好辅助线,充分利用相关几何知识解题。
(2)对称规律解题法
①从直线边界射入的粒子,又从同一边界射出时,出射速度与边界的夹角和入射速度与边界的夹角相等(如图甲所示)。
②在圆形磁场区域内,沿径向射入的粒子,一定沿径向射出(如图乙所示)。
(3)解决带电粒子在磁场中运动的临界问题,关键在于运用动态思维,寻找临界状态(一般是粒子运动轨迹与磁场边界相切或轨迹半径达到最大),常用方法如下:
①动态放缩法:定点粒子源发射速度大小不同、方向相同、比荷和电性都相同的粒子,速度越大半径越大,圆心在垂直初速度方向的直线上。
②旋转平移法:定点粒子源发射速度大小相等、方向不同、比荷和电性都相同的粒子,运动轨迹的圆心在以入射点为圆心、半径为R=的圆周上。
6.(2019·河南省郑州市一模)如图所示,边界OM与ON之间分布有垂直于纸面向里的匀强磁场,边界ON上有一粒子源S。某一时刻,从粒子源S沿平行于纸面,向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相等,经过一段时间有大量粒子从边界OM射出磁场。已知∠MON=30°,从边界OM射出的粒子在磁场中运动的最长时间等于T(T为粒子在磁场中运动的周期),则从边界OM射出的粒子在磁场中运动的最短时间为( )
A.T B.T
C.T D.T
答案 A
解析 粒子在磁场中做匀速圆周运动,入射点为S,出射点在OM直线上,出射点与S点的连线为轨迹的一条弦。由题意可知,粒子运动的最长时间等于T,则沿SN方向射入的粒子出射点D与S的连线为轨迹的直径,如图所示,设OS=d,则DS=OStan30°=d,粒子在磁场中做圆周运动的轨道半径为:r==d。当从边界OM射出的粒子在磁场中运动的时间最短时,圆心角最小,轨迹半径一定,则轨迹的弦最短,根据几何知识,作SE⊥OM,则SE为最短的弦,粒子从S到E的时间即最短,由几何知识有:SE=OSsin30°=d,由余弦定理得:cosθ==,且已知θ<180°,则:θ=120°,粒子在磁场中运动的最短时间为:tmin=T=T,故A正确。
7. (2019·福州高考模拟)(多选)如图所示,在圆心为O、半径为R的圆形区域内有垂直于纸面向外、磁感应强度大小为B的匀强磁场。一系列电子以不同的速率v(0,B错误;若增大磁感应强度B,由R=知离子在磁场中的运动半径减小,此时离子在磁场中运动的轨迹长度减小,速度大小不变,则运动时间减小,C错误;若B<,则R=>,该离子将从bc边射出,D正确。
4. (2019·安徽黄山二模)如图所示,垂直纸面向里的匀强磁场分布在等边三角形ABC内,D是AB边的中点,一群相同的带负电的粒子仅在磁场力作用下,从D点沿纸面以平行于BC边方向、大小不同的速率射入三角形内,不考虑粒子间的相互作用力,已知粒子在磁场中运动的周期为T,则下列说法中正确的是( )
A.若该粒子在磁场中经历时间为T,则它一定从BC边射出磁场
B.若该粒子在磁场中运动时间为T,则它一定从AC边射出磁场
C.速度小的粒子一定比速度大的粒子在磁场中运动时间长
D.若该粒子在磁场中的运动时间为T,则它一定从AB边射出磁场
答案 B
解析 若带电粒子刚好从BC边射出磁场,运动轨迹与BC边相切,可知圆心角为180°,粒子在磁场中经历时间为T;若带电粒子刚好从AC边射出磁场,运动轨迹与AC边相切,作图可得切点为C点,由几何关系可知圆心角为60°,粒子在磁场中运动的时间为T;若带电粒子从AB边射出磁场,可知圆心角为240°,粒子在磁场中的运动时间为T。所以若该粒子在磁场中的运动时间为T,则它一定从AB边射出磁场,A错误;若该粒子在磁场中的运动时间为T,小于T,则它一定从AC边射出磁场,B正确;若该粒子在磁场中的运动时间为T,即大于T小于T,则它一定从BC边射出磁场,D错误;若这些带电粒子都从AB边射出磁场,可知运动轨迹所对的圆心角都为240°,则粒子在磁场中经历时间都为T,故C错误。
5. (2019·陕西省三模)如图所示,半径为R的圆形区域内存在垂直于纸面向里的匀强磁场,现有比荷大小相等的甲、乙两粒子,甲以速度v1从A点沿直径AOB方向射入磁场,经过t1时间射出磁场,射出磁场时的速度方向与初速度方向间的夹角为60°;乙以速度v2从距离直径AOB为的C点平行于直径AOB方向射入磁场,经过t2时间射出磁场,其轨迹恰好通过磁场的圆心。不计粒子受到的重力,则( )
A.两个粒子带异种电荷
B.t1=t2
C.v1∶v2=∶1
D.两粒子在磁场中轨迹长度之比l1∶l2=∶1
答案 AC
解析 甲粒子向上偏转,根据左手定则可知甲粒子带正电,乙粒子向下偏转,根据左手定则可知乙粒子带负电,故A正确;粒子在磁场中运动的周期:T==,两粒子比荷相同,故两粒子在磁场中运动的周期相同,根据几何关系可知,甲、乙两粒子在磁场中运动的圆心角分别为60°和120°,甲在磁场中运动的时间t1=T=T,乙在磁场中运动的时间t2=T=T,即t1=t2,故B错误;设磁场区域圆的半径为R,由几何关系可知甲粒子做圆周运动的半径为R,乙粒子做圆周运动的半径为R,根据圆周运动的半径公式R=,知R与v成正比,即v1∶v2=∶1,故C正确;甲粒子在磁场中的轨迹长度l1=×2π×R=,乙粒子在磁场中的轨迹长度l2=×2πR=,所以两粒子在磁场中的轨迹长度之比为l1∶l2=∶2,故D错误。
6. (2019·江西高三九校3月联考)如图所示是一个半径为R的竖直圆形磁场区域,磁感应强度大小为B,磁感应强度方向垂直纸面向里。有一个粒子源在圆上的A点不停地发射出速率相同的带正电的粒子,带电粒子的质量均为m,电荷量均为q,运动的半径为r,在磁场中的轨迹所对应的圆心角为α。下列说法正确的是( )
A.若r=2R,则粒子在磁场中运动的最长时间为
B.若r=2R,粒子沿着与半径方向成45°角斜向下射入磁场,则有关系tan=成立
C.若r=R,粒子沿着磁场的半径方向射入,则粒子在磁场中的运动时间为
D.若r=R,粒子沿着与半径方向成60°角斜向下射入磁场,则圆心角α为150°
答案 BD
解析 若r=2R,粒子在磁场中运动的时间最长时,在磁场中的运动轨迹所对应的弦长最大,作出轨迹如图甲所示,因为r=2R,得圆心角α=60°,粒子在磁场中运动的最长时间tmax=T=·=,故A错误;若r=2R,粒子沿着与半径方向成45°角斜向下射入磁场,其运动轨迹如图乙所示,则根据几何关系,有tan===,故B正确;若r=R,粒子沿着磁场的半径方向射入,粒子运动轨迹如图丙所示,轨迹圆心角为90°,粒子在磁场中运动的时间t=T=·=,故C错误;若r=R,粒子沿着与半径方向成60°角斜向下射入磁场,轨迹如图丁所示,图中轨迹圆心与磁场圆心以及入射点和出射点连线构成菱形,圆心角α为150°,故D正确。
7. (2019·吉林省吉林市三模)如图所示,成30°角的OA、OB间有一垂直纸面向里的匀强磁场,OA边界上的S点有一电子源,在纸面内向各个方向均匀发射速率相同的电子,电子在磁场中运动的轨迹半径为r,周期为T。已知从OB边界射出的电子在磁场中运动的最短时间为,则下列说法正确的是( )
A.沿某一方向发射的电子,可能从O点射出
B.沿某一方向发射的电子,可能沿垂直于OB的方向射出
C.从OA边界射出的电子在磁场中运动的最长时间为
D.从OB边界射出的电子在磁场中运动的最长时间为
答案 BC
解析 电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:evB=m,解得r=,由于电子速率相同,则电子在磁场中做圆周运动的轨迹半径r相同,当出射点D与S点的连线垂直于OB时,弦SD最短,轨迹所对应的圆心角最小,则电子在磁场中运动的时间最短,tmin=T,则圆心角θ=60°,如图a所示,由几何知识知,在磁场中运动的时间最短的电子入射的方向垂直于OA,===2r,电子所有轨迹对应圆心的可能位置都应在以S为圆心、半径为=r的圆弧上,轨迹圆心恰好在OA上时,若磁场没有OB边界,电子将恰好通过O点,但由于OB边界的存在,过O点的电子的轨迹圆弧与OB有除O以外的另一个交点,如图b所示,说明电子到达O点前已经从另一交点飞出磁场,故A错误;由以上分析可知,当从S点射出的电子方向平行于OB时,其圆心恰好位于D点,此时电子将转过90°,恰好垂直于OB射出,其轨迹如图c所示,B正确;从OA边界射出的电子中,轨迹恰与OB相切时,在磁场中的运动轨迹最长,轨迹对应的圆心角最大,在磁场中运动的时间最长,如图d所示,由几何关系可得圆心角为120°,运动时间tmax=T=T,C正确;从OB边界射出的电子中,由几何关系可得,初速度方向沿OA方向的电子,在磁场中运动的时间最长,作出其运动轨迹如图e所示,可知该电子在磁场中运动的时间大于T,D错误。
8. (2019·江西新余四校高三第二次联考)如图所示,xOy
平面的一、二、三象限内存在垂直纸面向外,磁感应强度B=1 T的匀强磁场,ON为处于y轴负方向的弹性绝缘薄挡板,长度为9 m,M点为x轴正方向上一点,OM=3 m。现有一个比荷大小为=1.0 C/kg、可视为质点的带正电的小球(重力不计)从挡板下端N处小孔以不同的速度向x轴负方向射入磁场,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电荷量不变,已知小球最后都能经过M点,则小球射入的速度大小可能是( )
A.3 m/s B.3.75 m/s
C.4 m/s D.5 m/s
答案 ABD
解析 由题意,小球运动轨迹的圆心的位置一定在y轴上,所以小球若要经过M点,则其做圆周运动的半径r≥OM=3 m,而ON=9 m≤3r,所以小球可能与挡板ON碰撞一次,碰撞后以原速率弹回,速度反向,继续做圆周运动,第二段轨迹圆弧的圆心位置在O点或O点的上方,也可能小球与挡板ON没有碰撞,直接经过M点。由洛伦兹力提供向心力,有qvB=m,得v=。若小球与挡板ON碰撞一次,画出小球的运动轨迹如图1所示,设OO′=s,由几何关系得:r2=OM2+s2,s=3r-ON,联立得r1=3 m,r2=3.75 m,分别代入v=,解得v1=3 m/s,v2=3.75 m/s,故A、B正确;若小球没有与挡板ON碰撞,则小球的运动轨迹如图2所示,设OO′=s,由几何关系得:r=OM2+s2,s=ON-r3,联立得r3=5 m,代入v=得v3=5 m/s,故D正确。
二、计算题(本题共2小题,共36分,须写出规范的解题步骤)
9. (2019·东北三省三校二模)(16分)如图所示,在矩形区域Oabc内存在一个垂直于纸面向外,磁感应强度大小为B的匀强磁场,Oa边长为L,ab边长为L。先从O点沿着Ob方向垂直磁场射入各种速率的带电粒子,已知粒子的质量为m、带电量为q(粒子所受重力及粒子间相互作用忽略不计),求:
(1)垂直于ab边射出磁场的粒子的速率v;
(2)粒子在磁场中运动的最长时间tm。
答案 (1) (2)
解析 (1)粒子运动的轨迹如图,
设粒子做圆周运动的半径为R,
由几何关系可知:tanθ==,
得θ=,又sinθ=,则R=2L,
粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,则有qvB=m
解得v=。
(2)由圆周运动的知识可知T=,qvB=m
联立可得T=
由几何关系可知最大圆心角α=2θ=
可得粒子运动的最长时间tm=T=。
10. (2019·湖北荆门龙泉中学高三第五次学业检测)(20分)如图所示,一匀强磁场磁感应强度为B,方向垂直于纸面向里,其边界是半径为R的圆,AB为该圆的一条直径。在A点有一粒子源向圆平面内的各个方向发射质量为m、电量为-q的粒子,粒子重力不计。
(1)有一带电粒子以v1=的速度垂直于磁场进入圆形区域,恰从B点射出。求此粒子在磁场中运动的时间;
(2)若磁场的边界是绝缘弹性边界(粒子与边界碰撞后将以原速率反弹),某粒子沿半径方向射入磁场,经过2次碰撞后回到A点,则该粒子的速度为多大?
(3)若R=3 cm、B=0.2 T,在A点的粒子源向圆平面内的各个方向发射速度均为3×105 m/s、比荷为108 C/kg的粒子。试用阴影图画出粒子在磁场中能到达的区域,并求出该区域的面积(结果保留两位有效数字)。
答案 (1) (2) (3)见解析图c 9.0×10-4 m2
解析 (1)由qv1B=m得r1=2R
粒子的运动轨迹如图a所示,则由几何关系得α=
因为周期T=
所以该粒子在磁场中的运动时间t=T=。
(2)粒子运动情况如图b所示,则由几何关系得β=
r2=Rtanβ=R
由qv2B=m得v2=。
(3)粒子的轨道半径
r3==1.5 cm=R
粒子到达的区域如图c中的阴影部分所示,
区域面积为
S=πr+2×π(2r3)2-r≈9.0×10-4 m2。