【物理】2019届一轮复习人教版竖直平面内的圆周运动教案
2018-2019 年度高三一轮复习教案
课 题
竖直平面内的圆周运动
主备人
课 时
2课时
备课时间
上课时间
教 目标
1. 理解向心力的概念,能分析向心力的 ,能运用向心力公式进行计算.
2. 能分析水平面内、竖直平面内最高点和最低点的圆周运动问题.
教 重点
能分析水平面内、竖直平面内最高点和最低点的圆周运动问题.
教 难点
能分析水平面内、竖直平面内最高点和最低点的圆周运动问题.
教 方法
教师启发、引导, 生讨论、交流
教 媒体
投影片,多媒体辅助教 设备
教 过程
教 师 活 动
生活动
(1)汽车过凸形桥(设半径为r)在最高点时
公式:
① 当v=时,汽车对桥面的压力FN=0.
② 当0≤v
时,汽车将脱离桥面、发生危险.
(2)汽车过凹形桥(设半径为r)在最低点时
公式:
(3)过山车(设半径为r)在最高点时:
公式:
① 当v=时,车对桥面的压力FN=0.
② 当0≤v时,车安全经过
[汽车过拱桥] 一汽车通过拱形桥顶时速度为10 m/s,车对桥顶的压力为车重的,如果要使汽车在桥顶对桥面没有压力,车速至少为( )
A.15 m/s B.20 m/s C.25 m/s D.30 m/s
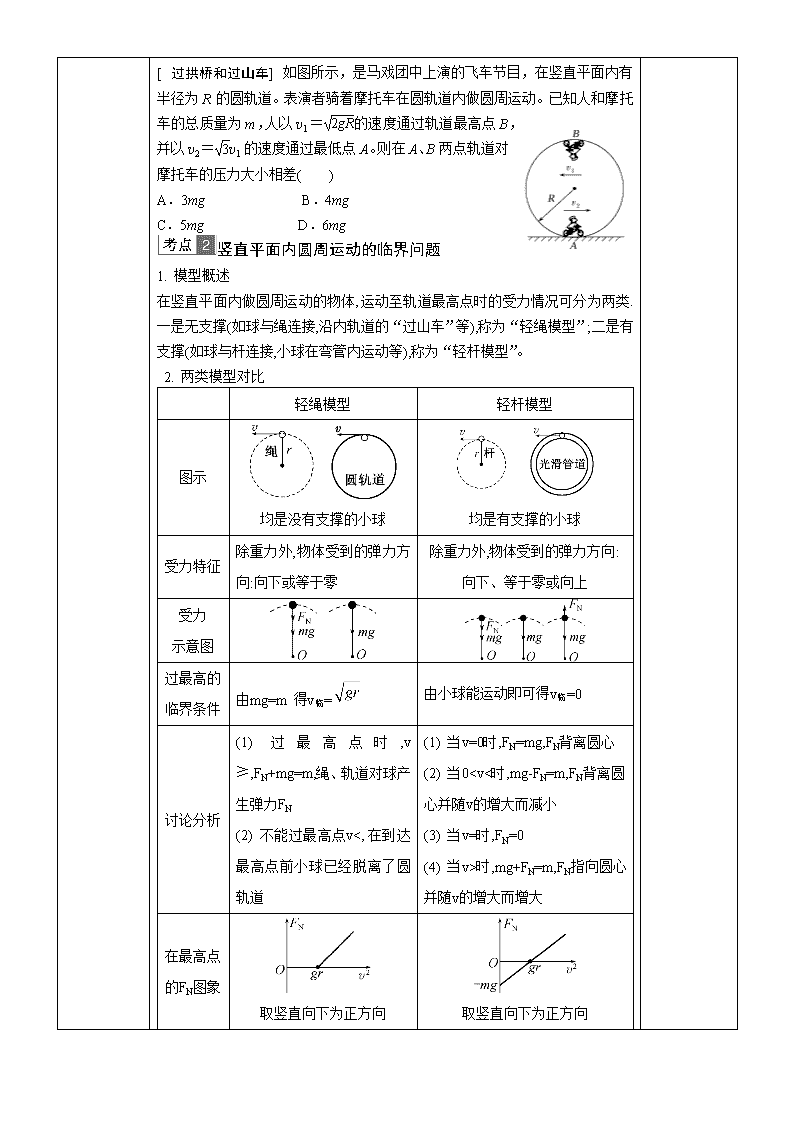
[过拱桥和过山车]如图所示,是马戏团中上演的飞车节目,在竖直平面内有半径为R的圆轨道。表演者骑着摩托车在圆轨道内做圆周运动。已知人和摩托车的总质量为m,人以v1=的速度通过轨道最高点B,并以v2=v1的速度通过最低点A。则在A、B两点轨道对摩托车的压力大小相差( )
A.3mg B.4mg
C.5mg D.6mg
竖直平面内圆周运动的临界问题
1. 模型概述
在竖直平面内做圆周运动的物体,运动至轨道最高点时的受力情况可分为两类.一是无支撑(如球与绳连接,沿内轨道的“过山车”等),称为“轻绳模型”;二是有支撑(如球与杆连接,小球在弯管内运动等),称为“轻杆模型”。
2. 两类模型对比
轻绳模型
轻杆模型
图示
均是没有支撑的小球
均是有支撑的小球
受力特征
除重力外,物体受到的弹力方向:向下或等于零
除重力外,物体受到的弹力方向:向下、等于零或向上
受力
示意图
过最高的
临界条件
由mg=m 得v临=
由小球能运动即可得v临=0
讨论分析
(1) 过最高点时,v≥,FN+mg=m,绳、轨道对球产生弹力FN
(2) 不能过最高点v<,在到达最高点前小球已经脱离了圆轨道
(1) 当v=0时,FN=mg,FN背离圆心
(2) 当0时,mg+FN=m,FN指向圆心并随v的增大而增大
在最高点
的FN图象
取竖直向下为正方向
取竖直向下为正方向
【典题演示1】长L=0.5 m质量可忽略的细杆,其一端可绕O点在竖直平面内转动,另一端固定着一个小球A。A的质量为m=2 kg,当A通过最高点时,如图所示,求在下列两种情况下杆对小球的作用力:
(1)A在最高点的速率为 m/s;
(2)A在最高点的速率为2m/s。
【拓展延伸】
在【典例】中若把细杆换成细绳,则在(1)(2)两种情况下小球能否过最高点?若能,此时细绳对小球的拉力为多大?
建模指导
分析竖直平面内圆周运动临界问题的思路
【典题演示2】 (2015·江西赣州模考)
一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,如图所示,则下列说法中正确的是 ( )
A. 小球过最高点时,杆所受到的弹力可以等于零
B. 小球过最高点的最小速度是
C. 小球过最高点时,杆对球的作用力一定随速度增大而增大
D. 小球过最高点时,杆对球的作用力一定随速度增大而减小
【跟踪训练】1. (2015·南通中 )如图所示,轻杆长3L,在杆两端分别固定质量均为m的球A和B,光滑水平转轴穿过杆上距球A为L处的O点,外界给系统一定能量后,杆和球在竖直平面内转动,球B运动到最高点时,杆对球B恰好无作用力.忽略空气阻力.则球B在最高点时( )
A. 球B的速度为零
B. 球A的速度大小为
C. 水平转轴对杆的作用力为1.5mg
D. 水平转轴对杆的作用力为2.5mg
【跟踪训练】2. (多选)(2017·常州中 )如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,则下列说法中正确的是( )
A. 小球通过最高点时的最小速度vmin=
B. 小球通过最高点时的最小速度vmin=0
C. 小球在水平线ab以下的管道中运动时,内侧管壁对小球一定无作用力
D. 小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力
板书设计
教 笔记