【物理】2020届一轮复习人教版专题03三大性质力及力的运算法则学案

【物理】2020届一轮复习人教版专题03三大性质力及力的运算法则学案

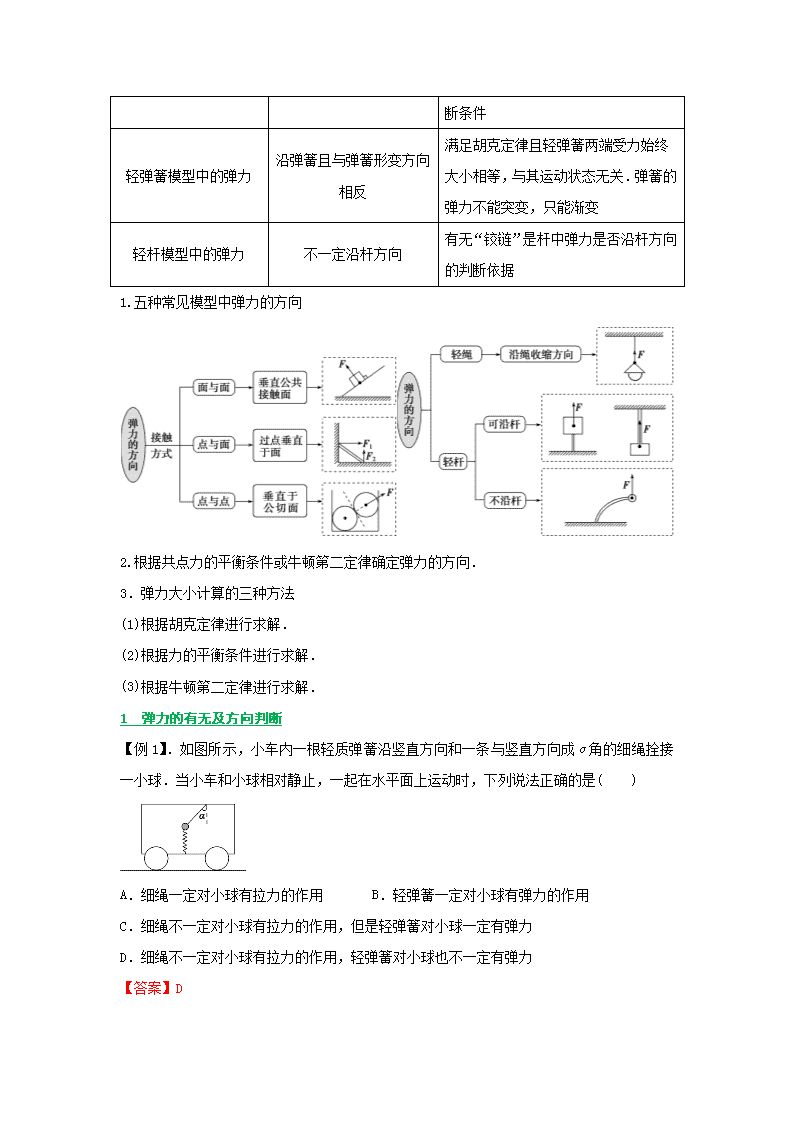
专题03 三大性质力及力的运算法则 ‎【专题导航】‎ 目录 热点题型一　弹力的分析与计算 1‎ ‎1　弹力的有无及方向判断 2‎ ‎2　轻绳模型中的“死结”和“活结”问题 3‎ ‎3.　轻弹簧模型中胡克定律的应用 4‎ ‎4　轻杆模型中的铰链问题 5‎ 热点题型二　摩擦力的分析与计算 7‎ ‎1．静摩擦力的有无和方向的判断方法 7‎ ‎2．摩擦力大小计算的思维流程 8‎ ‎（1）滑动摩擦力的分析与计算 9‎ ‎（2）静摩擦力的分析与计算 10‎ ‎3.摩擦力的“四类突变”问题 11‎ 静—静“突变” 11‎ 动—静“突变” 12‎ 动—动“突变” 13‎ 静→动“突变” 14‎ 热点题型三　力的合成 15‎ 热点题型四　力的分解 17‎ ‎【题型演练】 20‎ ‎【题型归纳】‎ 热点题型一　弹力的分析与计算 迁移角度 解决办法 易错警示 弹力的有无及方向判断 假设法或条件法 准确找到物体接触的公切面是判断方向的关键 轻绳模型中的拉力 沿绳且指向绳收缩的方向 有无“结点”‎ 是绳中张力是否相等的判断条件 轻弹簧模型中的弹力 沿弹簧且与弹簧形变方向相反 满足胡克定律且轻弹簧两端受力始终大小相等，与其运动状态无关．弹簧的弹力不能突变，只能渐变 轻杆模型中的弹力 不一定沿杆方向 有无“铰链”是杆中弹力是否沿杆方向的判断依据 ‎1.五种常见模型中弹力的方向 ‎2.根据共点力的平衡条件或牛顿第二定律确定弹力的方向．‎ ‎3．弹力大小计算的三种方法 ‎(1)根据胡克定律进行求解．‎ ‎(2)根据力的平衡条件进行求解．‎ ‎(3)根据牛顿第二定律进行求解．‎ ‎1　弹力的有无及方向判断 ‎【例1】．如图所示，小车内一根轻质弹簧沿竖直方向和一条与竖直方向成α角的细绳拴接一小球．当小车和小球相对静止，一起在水平面上运动时，下列说法正确的是(　　)‎ A．细绳一定对小球有拉力的作用 B．轻弹簧一定对小球有弹力的作用 C．细绳不一定对小球有拉力的作用，但是轻弹簧对小球一定有弹力 D．细绳不一定对小球有拉力的作用，轻弹簧对小球也不一定有弹力 ‎【答案】D ‎【解析】若小球与小车一起匀速运动，则细绳对小球无拉力；若小球与小车有向右的加速度a＝gtan α，则轻弹簧对小球无弹力，D正确．‎ ‎【变式1】(多选)如图所示为位于水平面上的小车，固定在小车上的支架的斜杆与竖直杆的夹角为θ，在斜杆 的下端固定有质量为m的小球．下列关于杆对球的作用力F的判断中，正确的是(　　)‎ A．小车静止时，F＝mgsin θ，方向沿杆向上 B．小车静止时，F＝mgcos θ，方向垂直于杆向上 C．小车向右匀速运动时，一定有F＝mg，方向竖直向上 D．小车向右匀加速运动时，一定有F＞mg，方向可能沿杆向上 ‎【答案】　CD ‎【解析】　小球受重力和杆的作用力F处于静止状态或匀速直线运动状态时，由力的平衡条件知，二力必等大反向，则F＝mg，方向竖直向上．小车向右匀加速运动时，小球有向右的恒定加速度，根据牛顿第二定律知，mg和F的合力应水平向右，如图所示．由图可知，F＞mg，方向可能沿杆向上，选项C、D正确．‎ ‎【变式2】(2019·西宁模拟)图中各物体均处于静止状态．图中画出了小球A所受弹力的情况，其中正确(　　)‎ ‎【答案】C ‎【解析】一般来讲轻质杆对物体的弹力不一定沿着杆的方向，选项A 中小球只受重力和杆的弹力且处于静止状态，由二力平衡可得小球受到的弹力应竖直向上，所以A错．选项B中，如果左边的绳有拉力的话，竖直向上的那根绳就会发生倾斜，所以左边的绳没有拉力，故B错．对于球与面接触的弹力方向，过接触点垂直于接触面(即在接触点与球心的连线上)，即D中大半圆对小球的支持力FN2应是沿着过小球与圆弧接触点的半径且指向圆心的弹力，所以D错．球与球相接触的弹力方向，垂直于过接触点的公切面(即在两球心的连线上)，而指向受力物体，所以C正确．‎ ‎2　轻绳模型中的“死结”和“活结”问题 ‎【例2】．(多选) 如图所示，用滑轮将质量为m1、m2的两物体悬挂起来，忽略滑轮和绳的重力及一切摩擦，使得0＜θ＜180°，整个系统处于平衡状态，关于m1、m2的大小关系应为(　　)‎ A．m1必大于m2　 B．m1必大于C．m1可能等于m2 D．m1可能大于m2‎ ‎【答案】BCD ‎【解析】选BCD.结点O受三个力的作用，如图所示，系统平衡时F1＝F2＝m1g，F3＝m2g，所以2m1gcos ＝m2g，m1＝，所以m1必大于.当θ＝120°时，m1＝m2；当θ＞120°时，＞m2；当θ＜120°时，m1＜m2，故B、C、D选项正确．‎ ‎【变式】如图所示，两个轻环a和b套在位于竖直面内的一段固定圆弧上；一细线穿过两轻环，其两端各系一质量为m的小球．在a和b之间的细线上悬挂一小物块．平衡时，a、b间的距离恰好等于圆弧的半径．不计所有摩擦．小物块的质量为(　　)‎ A. B.m C．m D．2m ‎【答案】　C ‎【解析】　如图所示，圆弧的圆心为O，悬挂小物块的点为c，由于ab＝R，则△aOb 为等边三角形，同一条细线上的拉力相等，FT＝mg，合力沿Oc方向，则Oc为角平分线，由几何关系知，∠acb＝120°，故细线的拉力的合力与物块的重力大小相等，则每条细线上的拉力FT＝G＝mg，所以小物块质量为m，故C对．‎ ‎3.　轻弹簧模型中胡克定律的应用 ‎【例3】.(2018·高考全国卷Ⅰ)如图，轻弹簧的下端固定在水平桌面上，上端放有物块P，系统处于静止状态．现用一竖直向上的力F作用在P上，使其向上做匀加速直线运动．以x表示P离开静止位置的位移，在弹簧恢复原长前，下列表示F和x之间关系的图象可能正确的是(　　)‎ ‎【答案】A ‎【解析】假设物块静止时弹簧的压缩量为x0，则由力的平衡条件可知kx0＝mg，在弹簧恢复原长前，当物块向上做匀加速直线运动时，由牛顿第二定律得F＋k(x0－x)－mg＝ma，由以上两式解得F＝kx＋ma，显然F和x为一次函数关系，且在F轴上有截距，则A正确，B、C、D错误．‎ ‎【变式】如图所示，质量均为m的A、B两球，由一根劲度系数为k的轻弹簧连接静止于半径为R的光滑 半球形碗中，弹簧水平，两球间距为R且球半径远小于碗的半径．则弹簧的原长为(　　)‎ A.＋R　　　　　　　B.＋R C.＋R D.＋R ‎【答案】D ‎【解析】以A球为研究对象，小球受重力、弹簧的弹力和碗的支持力，如图所示．‎ 由平衡条件，得：tan θ＝＝ 解得：x＝ 根据几何关系得：cos θ＝＝，则tan θ＝，‎ 所以x＝＝ 故弹簧原长x0＝＋R，故D正确．‎ ‎4　轻杆模型中的铰链问题 ‎【例4】．(2019·潍坊模拟)如图甲所示，轻杆OB可绕B点自由转动，另一端O点用细绳OA拉住，固定在左侧墙壁上，质量为m的重物用细绳OC悬挂在轻杆的O点，OA与轻杆的夹角∠BOA＝30°.乙图中水平轻杆OB一端固定在竖直墙壁上，另一端O装有小滑轮，用一根绳跨过滑轮后悬挂一质量为m的重物，图中∠BOA＝30°，求：‎ ‎(1)甲、乙两图中细绳OA的拉力各是多大？‎ ‎(2)甲图中轻杆受到的弹力是多大？‎ ‎(3)乙图中轻杆对滑轮的作用力是多大？‎ ‎【解析】(1)由于甲图中的杆可绕B转动，是转轴杆(是“活杆”)，故其受力方向沿杆方向，O点的受力情况如图(a)所示，则O点所受绳子OA的拉力FT1、杆的弹力FN1的合力与物体的重力是大小相等、方向相反的，在直角三角形中可得，FT1＝＝2mg；乙图中是用一细绳跨过滑轮悬挂物体的，由于O点处是滑轮，它只是改变绳中力的方向，并未改变力的大小，且AOC是同一段绳子，而同一段绳上的力处处相等，故乙图中绳子拉力为F′T1＝F′T2＝mg.‎ ‎(2)由图(a)可知，甲图中轻杆受到的弹力为F′N1＝FN1＝＝mg.‎ ‎(3)对乙图中的滑轮受力分析，如图(b)所示，由于杆OB不可转动，所以杆所受弹力的方向不一定沿OB方向．即杆对滑轮的作用力一定与两段绳的合力大小相等，方向相反，由图(b)可得，F2＝2mgcos 60°＝mg，则所求力F′N2＝F2＝mg.‎ ‎【答案】(1)2mg　mg　(2)mg　(3)mg ‎【变式】(2019·天津市南开中学月考)如图为两种形式的吊车的示意图，OA为可绕O点转动的轻杆，重量不计，AB为缆绳，当它们吊起相同重物时，杆OA在图(a)、(b)中的受力分别为Fa、 Fb，则下列关系正确的是(　　)‎ A．Fa＝Fb B．Fa>Fb C．Fa

查看更多