2018届二轮复习　曲线运动课件（55张）全国通用

2018届二轮复习　曲线运动课件（55张）全国通用

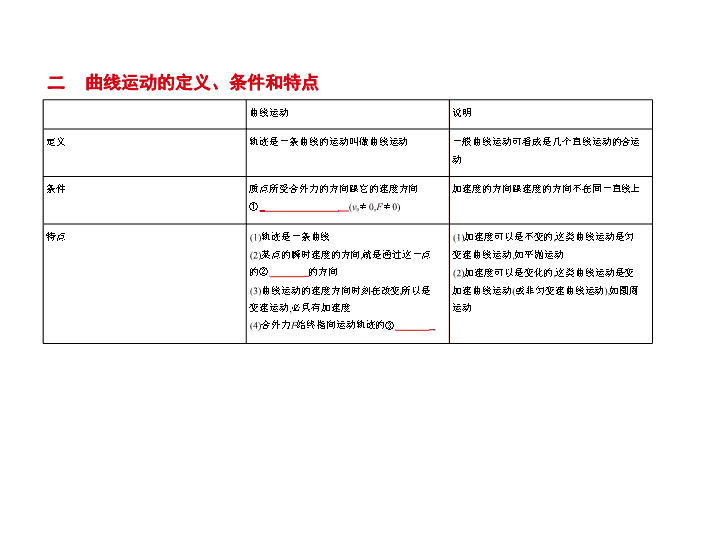
一    质点运动类型的分类及条件 考点一    运动的合成与分解 知识清单 < 基础知识 > 曲线运动 说明 定义 轨迹是一条曲线的运动叫做曲线运动 一般曲线运动可看成是几个直线运动的合运 动 条件 质点所受合外力的方向跟它的速度方向 ①     不在同一直线上     ( v 0 ≠ 0, F ≠ 0) 加速度的方向跟速度的方向不在同一直线上 特点 (1)轨迹是一条曲线 (2)某点的瞬时速度的方向,就是通过这一点 的② 　切线     的方向 (3)曲线运动的速度方向时刻在改变,所以是 变速运动,必具有加速度 (4)合外力 F 始终指向运动轨迹的③ 　内侧      (1)加速度可以是不变的,这类曲线运动是匀 变速曲线运动,如平抛运动 (2)加速度可以是变化的,这类曲线运动是变 加速曲线运动(或非匀变速曲线运动),如圆周 运动 二    曲线运动的定义、条件和特点 三　 运动的合成与分解 1.合运动与分运动的关系 2.运动的合成与分解的运算法则 运动的合成与分解是指描述运动的各物理量即位移、速度、加速度的 合成与分解。由于它们都是矢量,所以合成与分解都遵循 ⑦ 　平行四边形定则     。 3.运动的合成与分解 已知分运动求合运动,叫做运动的合成;已知合运动求分运动,叫做运动 等时性 各分运动经历的时间与合运动经历的时间④ 　相同     独立性 一个物体同时参与几个分运动,各分运动⑤ 　独立     进行,不受其他分 运动的影响 等效性 各分运动叠加起来与合运动有⑥ 　相同     的效果 的分解。 分运动与合运动是一种⑧ 　等效替代     关系,运动的合成与分解是研究 曲线运动的一种基本方法。 一、物体做曲线运动的分析   二、合运动的性质和轨迹 合运动的性质和轨迹由合初速度( v 合初 )和合加速度( a 合 )共同决定。 < 重点难点 >   例 　如图甲所示,在一端封闭、长约1 m的玻璃管内注满清水,水中放一 个蜡块,将玻璃管的开口端用胶塞塞紧。然后将这个玻璃管倒置,在蜡 块沿玻璃管上升的同时,将玻璃管水平向右移动。假设从某时刻开始计 时,蜡块在玻璃管内每1 s上升的距离都是10 cm,玻璃管向右匀加速平 移,每1 s通过的水平位移依次是2.5 cm、7.5 cm、12.5 cm、17.5 cm。图 乙中 y 表示蜡块竖直方向的位移, x 表示蜡块随玻璃管通过的水平位移, t = 0时蜡块位于坐标原点。   (1)请在图乙中画出蜡块4 s内的轨迹; (2)求出玻璃管向右平移的加速度大小; (3)求 t =2 s时蜡块的速度 v 的大小。 解题导引   解析 　(2)根据匀变速直线运动的规律Δ x = at 2 ,得玻璃管向右平移的加 速度 a =   =5 × 10 -2 m/s 2 。 (3) t =2 s时,蜡块在竖直方向和水平方向的分速度分别为 v y =   =0.1 m/s, v x = at =0.1 m/s。 此时蜡块的速度即合速度 v =   =   m/s。   答案 　(1)如图所示　(2)5 × 10 -2 m/s 2 　(3)   m/s 一    平抛运动 1.平抛运动 (1)定义:水平抛出的物体只在① 　重力     作用下的运动叫做平抛运 动。 (2)性质:加速度为② 　重力加速度 g      的匀变速曲线运动,轨迹是抛物 线。 (3)研究方法:平抛运动可以分解为水平方向上的③ 　匀速直线     运动 和竖直方向上的④ 　自由落体     运动。 (4)运动时间和射程 t =   仅取决于竖直下落的高度;射程 x = v 0   取决于竖直下落的高度 考点二    平抛运动 < 基础知识 > 和初速度。 2.平抛运动的规律 以抛出点为坐标原点,以初速度 v 0 方向为 x 轴正方向,竖直向下为 y 轴正方 向,如图所示,则有   水平方向分速度: v x = v 0 竖直方向分速度: v y = gt 合速度大小: v =   tan θ =   ( θ 为速度与水平方向的夹角) 水平方向分位移: x '= v 0 t 竖直方向分位移: y '=   gt 2 合位移: x 合 =   tan β =   ( β 为位移与水平方向的夹角) 二    斜抛运动 1.斜抛运动的定义 将物体以速度 v 0 斜向上方或斜向下方抛出,物体只在⑤ 　重力     作用下 的运动。 2.运动性质 加速度为⑥ 　重力加速度 g      的匀变速曲线运动,轨迹为抛物线。 3.基本特点 (以斜向上抛为例说明,如图所示)   (1)水平方向: v 0 x =⑦      v 0 ·cos θ      , F 合 x =0。 (2)竖直方向: v 0 y =⑧      v 0 ·sin θ      , F 合 y = mg 。 一、平抛运动的分解与实例 方法 内容 实例 斜面 求小球平抛时间 总结 分解 速度 水平 v x = v 0 竖直 v y = gt 合速度 v =     解:如图, v y = gt , tan θ =   =   , 故 t =   分解速度, 构建速度 三角形 分解 位移 水平 x = v 0 t 竖直 y =   gt 2 合位移 x 合 =     解:如图, x = v 0 t , y =   gt 2 , 而tan θ =   , 联立得 t =   分解位移, 构建位移 三角形 < 重点难点 > 例1     (2014浙江理综,23,16分)如图所示,装甲车在水平地面上以速度 v 0 = 20 m/s沿直线前进,车上机枪的枪管水平,距地面高为 h =1.8 m。在车正 前方竖直立一块高为两米的长方形靶,其底边与地面接触。枪口与靶距 离为 L 时,机枪手正对靶射出第一发子弹,子弹相对于枪口的初速度为 v = 800 m/s。在子弹射出的同时,装甲车开始匀减速运动,行进 s =90 m后停 下。装甲车停下后,机枪手以相同方式射出第二发子弹。(不计空气阻 力,子弹看成质点,重力加速度 g =10 m/s 2 ) (1)求装甲车匀减速运动时的加速度大小; (2)当 L =410 m时,求第一发子弹的弹孔离地的高度,并计算靶上两个弹 孔之间的距离; (3)若靶上只有一个弹孔,求 L 的范围。 解题导引   解析 　(1)装甲车匀减速运动时的加速度大小 a =   =   m/s 2 (2)第一发子弹飞行时间 t 1 =   =0.5 s 弹孔离地高度 h 1 = h -   g   =0.55 m 第二发子弹的弹孔离地的高度 h 2 = h -   g   =1.0 m 两弹孔之间的距离Δ h = h 2 - h 1 =0.45 m (3)第一发子弹打到靶的下沿时,装甲车离靶的距离为 L 1 L 1 =( v 0 + v )   =492 m 第二发子弹打到靶的下沿时,装甲车离靶的距离为 L 2 L 2 = v   + s =570 m L 的范围492 m< L ≤ 570 m   答案 　(1)   m/s 2 (2)0.55 m　0.45 m (3)492 m< L ≤ 570 m 二、平抛运动的两个推论 推论一　做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其末 速度方向与水平方向的夹角为 θ ,位移与水平方向的夹角为 φ ,则tan θ =2 tan φ 。 证明:如图甲所示,由平抛运动规律得 tan θ =   =   ,tan φ =   =     =   , 所以tan θ =2 tan φ 。   推论二　做平抛(或类平抛)运动的物体任意时刻的瞬时速度的反向延 长线一定通过此时水平位移的中点。如图乙中所示 B 点。 证明:设平抛物体的初速度为 v 0 ,从原点 O 到 A 点的时间为 t , A 点坐标为 ( x , y ), B 点坐标为( x ',0),则 x = v 0 t , y =   gt 2 , v ⊥ = gt ,又tan θ =   =   ,解得 x '=   。 即末状态速度反向延长线与 x 轴的交点 B 必为此刻水平位移的中点。 注意     (1)在平抛运动过程中,位移矢量与速度矢量永远不会同线。 (2)推论一中的tan θ =2 tan φ ,但不能误认为 θ =2 φ 。 例2     (2016吉林实验中学一模)如图所示,从倾角为 θ 的足够长的斜面顶 端 P 以速度 v 0 平抛出一个小球,落在斜面上某处 Q 点,小球落在斜面上的 速度与斜面的夹角为 α ,若把初速度变为3 v 0 ,小球仍落在斜面上,则以下 说法正确的是   (　　)   A.夹角 α 将变大 B.夹角 α 与初速度大小无关 C.小球在空中的运动时间不变 D. P 、 Q 间距是原来间距的3倍   解析 　由图可知,tan ( α + θ )=   =   ,而tan θ =   =   =   ,可得tan ( α + θ ) =2 tan θ ,则知 α 大小与初速度大小无关,大小不变,选项A错误,B正确;斜 面倾角的正切值tan θ =   ,得 t =   ,若初速度变为原来的3倍,其运 动时间变为原来的3倍,选项C错误; P 、 Q 间距 s =   =   ,若初速度变 为原来的3倍,则时间 t 变为原来的3倍,则 P 、 Q 间距变为原来的9倍,选项 D错误。     答案     B 一    描述圆周运动的物理量 考点三    圆周运动 < 基础知识 > 定义、意义 公式、单位   (1)描述做圆周运动的物体① 　运动快慢     的物理量( v ) (2)是② 　矢量     ,方向和半径垂直,和圆周③ 　相切     a. v =   , v =   b.单位:m/s   (1)描述物体④ 　绕圆心转动     快慢的物理量( ω ) (2)是矢量,但中学阶段不研究其方向 a. ω =   , ω =   b.单位:rad/s   (1)周期是物体沿圆周⑤ 　匀速运动一周     的时间( T );周期的倒数叫做频率( f ) (2)转速是物体单位时间内转过的圈数( n ) a. T =   ,单位:s b. f =   ,单位:Hz c. n 的单位:r/s、r/min   (1)描述速度⑥ 　方向     变化快慢的物理量( a ) (2)方向指向圆心 a. a =   = rω 2 b.单位:m/s 2   (1)作用效果是产生⑦ 　向心     加速度 (2)方向始终指向⑧ 　圆心     a. F = ma =   = mω 2 r = mωv b.单位:N   (1) T =   　(2) v = rω =   r =2π fr (3) a =   = rω 2 = ωv =   =4π 2 f 2 r 　(4) t =   · T 二    离心现象 当提供的向心力小于所需向心力时,物体将远离原来的轨道的现象叫离 心现象。 从力的角度分析物体的运动: 1.匀速圆周运动: F 合 = mrω 2 。 2.离心运动: F 合 < mrω 2 。 3.向心运动: F 合 > mrω 2 。 一、做圆周运动的常见模型 单摆   ①部分圆周运动 ②非匀速圆周运动 ③ F 合 =   ,只有在最低点指向圆心 ④在最低点: v ≠ 0时, T > G ; v =0时, T = G 竖直平 面内的 圆周运动 方法技巧——方法3中有详细介绍 火车转弯   F 向 = G tan θ 或 F 向 = N sin θ 或 F 向 = mω 2 r 圆锥摆   F 向 = G tan θ 或 F 向 = mω 2 r r = l sin θ < 重点难点 > 二、常见传动装置及其特点 1.共轴传动 A 点和 B 点在同轴的一个圆盘上,如图甲,圆盘转动时,它们的线速度、角 速度、周期存在以下定量关系: ω A = ω B ,   =   , T A = T B ,并且转动方向相同。   甲        乙 2.皮带传动 A 点和 B 点分别是两个轮子边缘上的点,两个轮子用皮带连起来,并且皮 带不打滑。如图乙,轮子转动时,它们的线速度、角速度、周期存在以 下定量关系: v A = v B ,   =   ,   =   ,并且转动方向相同。 A 点和 B 点分别是两个齿轮边缘上的点,两个齿轮轮齿啮合。如图,齿轮 转动时,它们的线速度、角速度、周期存在以下定量关系: v A = v B ,   =   =   ,   =   =   。 式中 n 1 、 n 2 分别表示两齿轮的齿数。两点转动方向相反。 注意　在处理传动装置中各物理量间的关系时,关键是确定其相同的量 (线速度或角速度),再由描述圆周运动的各物理量间的关系,确定其他各 量间的关系。 3.齿轮传动 　 小船过河问题的处理方法 小船在有一定流速的水中过河时,实际上参与了两个方向的分运动,即 随水流的运动(水冲船的运动)和船相对静水的运动,船的实际运动是合 运动。 方法 1 方法技巧 例1 　一条宽度为 l 的河流,已知船在静水中的速度为 v 船 ,水流速度为 v 水 。 那么: (1)怎样渡河时间最短? (2)若 v 船 > v 水 ,怎样渡河位移最小? (3)若 v 船 < v 水 ,怎样渡河船漂下的距离最短?   解析 　(1)如图甲所示,设船头斜向上游与河岸成任意角 θ ,这时船速在 垂直于河岸方向的速度分量为 v 1 = v 船 sin θ ,渡河所需的时间为 t =   =   。 可以看出: l 、 v 船 一定时, t 随sin θ 增大而减小;当 θ =90 ° 时,sin θ =1(最大)。 所以可得,船头与河岸垂直时渡河时间最短,即 t min =   。 (2)如图乙所示,渡河的最小位移即河的宽度。为了使渡河位移等于 l ,必 须使船的合速度 v 的方向与河岸垂直。这时船头应指向河的上游,并与 河岸成一定的角度 θ 。根据三角函数关系有 v 船 cos θ - v 水 =0,得cos θ =   ,即 θ =arccos   。 因为0 ≤ cos θ <1,所以只有在 v 船 > v 水 时,船才有可能垂直河岸横渡。 (3)如果水流速度大于船在静水中的航行速度,则不论船的航向如何,总 是被水冲向下游。怎样才能使船漂下的距离最短呢?如图丙所示,设船 头( v 船 方向)与河岸成 θ 角。合速度 v 合 与河岸成 α 角。可以看出: α 角越大, 船漂下的距离 x 越短。那么,在什么条件下 α 角最大呢?以 v 水 的末端为圆 心、 v 船 大小为半径画圆,当 v 合 与圆相切时, α 角最大,根据cos θ =   可得, 船头与河岸的夹角应为 θ =arccos   。 船漂下的最短距离为 x min =( v 水 - v 船 cos θ )·   , 此时渡河的最短位移为 s =   =   。   答案 　见解析 　 绳子末端速度分解的处理方法 1.绳子末端运动速度的分解,应按运动的实际效果进行。 2.速度投影定理:两个物体在不可伸长的绳(或杆)的连接下沿不同方向 运动,则两物体沿绳(或杆)方向的分速度相同。 例如在图中,人用绳子通过定滑轮拉物体 A ,当人以速度 v 0 匀速后退拉绳 时,求物体 A 的速度。   方法 2 首先要分析物体 A 的运动与人拉绳的运动之间有什么样的关系。物体 A 的运动(即绳的末端的运动)可看做两个分运动的合成: (1)沿绳的方向被牵引,绳长缩短,绳长缩短的速度即等于 v 0 ; (2)垂直于绳以定滑轮为圆心的摆动,它不改变绳长。 这样就可以求得物体 A 的速度 v A =   。当物体 A 向左移动时, θ 将逐渐 变大, v A 逐渐变大。虽然人做匀速运动,但物体 A 却在做变速运动。 例2 　人用绳子通过定滑轮拉物体 A , A 穿在光滑的竖直杆上,当以速度 v 0 匀速地拉绳使物体 A 到达如图所示位置时,绳与竖直杆的夹角为 θ ,则物 体 A 实际运动的速度是   (　　) 　       A. v 0 sin θ 　    B.   　    C. v 0 cos θ 　    D.   解题导引   解析 　由运动的合成与分解可知,物体 A 参与这样的两个分运动,一个 是沿着与它相连接的绳子的运动,另一个是垂直于绳子斜向上的运动。 而物体 A 实际运动是沿着竖直杆向上运动,此运动就是物体 A 的合运动, 合速度与分速度之间的关系如图所示。由三角函数知识可得 v A =   , 所以D选项是正确的。     答案     D 　 圆周运动临界问题的处理 1.“火车转弯”问题 在火车转弯处,让外轨高于内轨,如图所示,转弯时火车所需向心力由重 力和弹力的合力提供。   设车轨间距为 L ,两轨高度差为 h ,火车转弯半径为 R ,质量为 M 的火车运行 时应当有多大的速度? 方法 3 据三角形边角关系知sin θ =   ,对火车的受力情况分析得tan θ =   。 因为 θ 角很小,所以sin θ =tan θ ,故   =   ,所以向心力 F 向 = F 合 =   Mg 。又因 为 F 合 = Mv 2 / R ,所以车速 v =   。 由于铁轨建成后 h 、 L 、 R 各量是确定的,故火车转弯时的车速应是一个 定值,否则将对铁轨有不利影响,如: (1)火车在弯道处的速度大于   ,重力和支持力的合力不足以充当火 车做圆周运动需要的向心力,火车要挤压外侧车轨,外侧车轨受挤压发 生形变产生弹力,补充不足的向心力。 (2)火车在弯道处的速度小于   ,重力和支持力的合力大于火车做圆 周运动需要的向心力,火车就要挤压内侧车轨,内侧车轨受挤压发生形 变产生弹力,抵消一部分重力和支持力的合力。 例3 　表格所示是铁路设计人员技术手册中弯道半径 r 及与之对应的轨 道高度差 h 的部分数据。 (1)根据表中的数据,试写出 h 和 r 关系的表达式,并求出当 r =440 m时, h 的设计值; (2)铁路建成后,火车通过弯道时,为保证安全,要求内、外轨道均不向车 轮施加侧向压力,已知我国铁路内、外轨的间距设计值为 L =1 435 mm, 结合表中数据,算出我国火车的转弯速率 v (以km/h为单位,结果取整数, 路轨倾角很小时,正切值按正弦值处理)。 弯道半径 r /m 660 330 220 165 132 110 内、外轨 高度差 h /mm 50 100 150 200 250 300 解题导引   解析 　(1)分析表中数据得每组的 h 与 r 之积均等于常数,有 h 1 r 1 =660 × 50 × 10 -3 m 2 =33 m 2 即 hr =33 m 2 当 r =440 m时,将数据代入上式可得 h =75 mm。 (2)转弯时,当内外轨对车轮没有侧向压力时,火车的受力如图所示: 由牛顿第二定律得 mg tan α = m   因为 α 很小,有tan α ≈ sin α =   由以上两式可得 v =   =   m/s ≈ 15 m/s=54 km/h。   答案 　(1)见解析　(2)54 km/h 2.对竖直平面内圆周运动的分析 物体在竖直平面内做的圆周运动是一种典型的变速曲线运动,该类运动 常有临界问题,题目中常伴有“最大”“最小”“刚好”等词语,常分 析两种模型——轻绳模型和轻杆模型,分析比较如下。 轻绳模型 轻杆模型 常见 类型   均是没有支撑的小球   均是有支撑的小球 过最高 点的临 界条件 由 mg = m   得 v 临 =   由小球恰能运动即可得 v 临 =0 讨论 分析 (1)过最高点时, v ≥   , F N + mg = m   ,绳、轨 道对球产生弹力 F N (2)不能过最高点, v <   ,在到达最高点前小 球已经脱离了圆轨道 (1)当 v =0时, F N = mg , F N 为支持力,沿半径背离圆 心 (2)当0< v <   时, mg - F N = m   , F N 背离圆心,随 v 的增大而减小 (3)当 v =   时, F N =0 (4)当 v >   时, F N + mg = m   , F N 指向圆心并随 v 的增大而增大 例4     (2017广东汕头二模,17)如图甲,小球用不可伸长的轻绳连接后绕 固定点 O 在竖直面内做圆周运动,小球经过最高点时的速度大小为 v ,此 时绳子的拉力大小为 T ,拉力 T 与速度 v 的关系如图乙所示,图像中的数据 a 和 b 包括重力加速度 g 都为已知量,以下说法正确的是   (　　)   A.数据 a 与小球的质量有关 B.数据 b 与圆周轨道半径有关 C.比值   只与小球的质量有关,与圆周轨道半径无关 D.利用数据 a 、 b 和 g 能够求出小球的质量和圆周轨道半径 解题导引   解析 　在最高点对小球受力分析,由牛顿第二定律有 T + mg = m   ,可得 T = m   - mg ,图乙中横轴截距为 a ,则有0= m   - mg ,得 g =   ,则 a = gR ;图线过点 (2 a , b ),则 b = m   - mg ,可得 b = mg ,则   =   ,A、B、C错。由 b = mg 得 m =   ,由 a = gR 得 R =   ,则D正确。   答案     D 　 圆周运动中的多解问题 大多数物理问题具有单一的确定解,然而有些物理问题的解并不唯一, 即有多个解。对于这类物理问题,倘若物理过程不清,便可能只得出特 解,而导致漏解。 方法 4 例5     [2014天津理综,9(1),4分]半径为 R 的水平圆盘绕过圆心 O 的竖直轴 匀速转动, A 为圆盘边缘上一点。在 O 的正上方有一个可视为质点的小 球以初速度 v 水平抛出时,半径 OA 方向恰好与 v 的方向相同,如图所示。 若小球与圆盘只碰一次,且落在 A 点,重力加速度为 g ,则小球抛出时距 O 的高度 h = 　　     ,圆盘转动的角速度大小 ω = 　　     。     解析     小球做平抛运动: h =   gt 2 、 R = vt ,解得 h =   。由题意知 ωt =2π × n ( n ∈N * ),故联立 R = vt 可得 ω =   ( n ∈N * )。   答案               ( n ∈N * )