【物理】2020届一轮复习教科版第3章第2讲牛顿第二定律两类动力学问题作业
练案[8]第三章 牛顿运动定律
第2讲 牛顿第二定律 两类动力学问题
一、选择题(本题共8小题,1~5题为单选,6~8题为多选)
1.(2019·江苏泰州联考)有时候投篮后篮球会停在篮网里不掉下来,弹跳好的同学就会轻拍一下让它掉下来。我们可以把篮球下落的情景理想化:篮球脱离篮网静止下落,碰到水平地面后反弹,如此数次落下和反弹。若规定竖直向下为正方向,碰撞时间不计,空气阻力大小恒定,则下列图象中可能正确的是( A )
[解析] 篮球向下运动时,受重力和空气阻力作用,根据牛顿第二定律有:mg-f=ma1,解得a1=g-;篮球反弹向上运动时,受重力和空气阻力作用,根据牛顿第二定律有:mg+f=ma2,解得a2=g+,联立得:a1
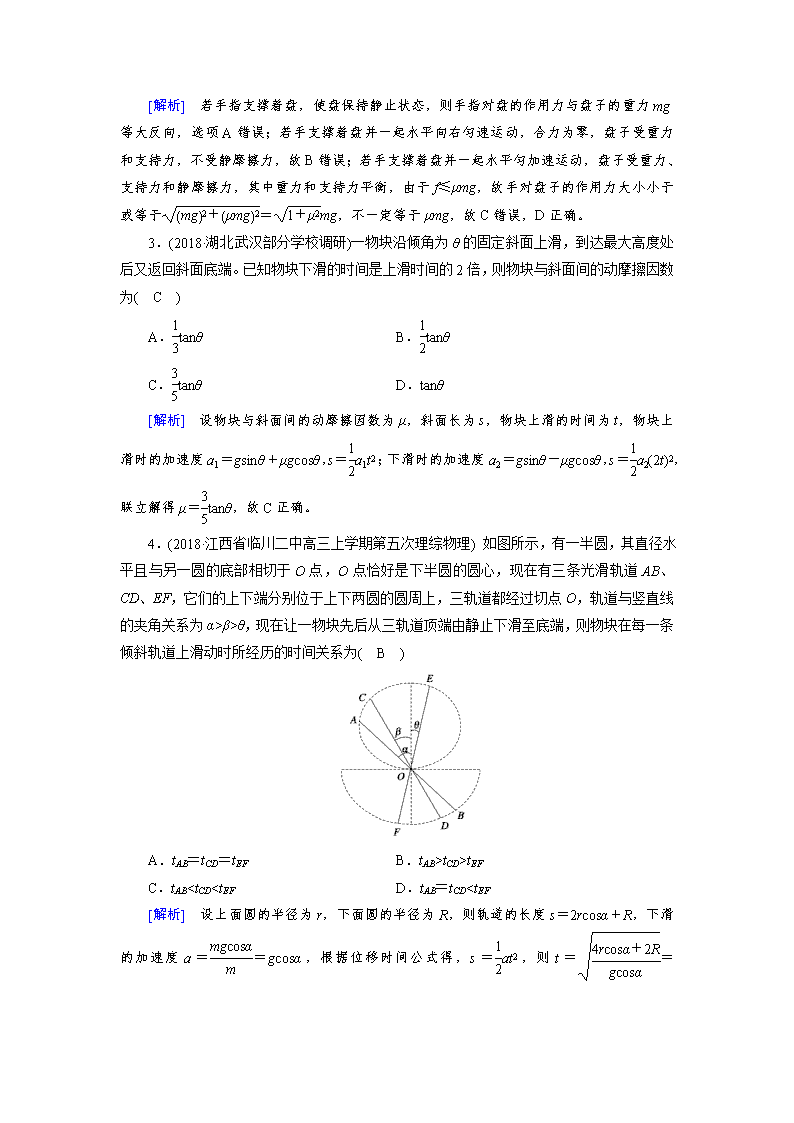
β>θ,现在让一物块先后从三轨道顶端由静止下滑至底端,则物块在每一条倾斜轨道上滑动时所经历的时间关系为( B )
A.tAB=tCD=tEF B.tAB>tCD>tEF
C.tABβ>θ,则tAB>tCD>tEF,故B正确,A、C、D错误。
5.(2019·嘉兴模拟)绰号“威龙”的第五代制空战机歼-20具备高隐身性、
高机动性能力,为防止极速提速过程中飞行员因缺氧晕厥,歼-20新型的抗荷服能帮助飞行员承受最大9倍重力加速度。假设某次垂直飞行测试实验中,歼-20加速达到50m/s后离地,而后开始竖直向上飞行试验。该飞机在10s内匀加速到3060km/h,匀速飞行一段时间后到达最大飞行高度18.5km。假设加速阶段所受阻力恒定,约为重力的0.2。已知该歼-20质量为20吨,声速为340m/s,忽略战机因油耗等导致质量的变化。则下列说法正确的是( B )
A.本次飞行测试的匀速阶段运行时间为26.5s
B.加速阶段系统的推力为1.84×106N
C.加速阶段时飞行员有晕厥可能
D.飞机在匀速阶段时爬升高度为14.25km
[解析] 加速阶段初速度v0=50m/s,末速度v=3060km/h=850m/s,根据v=v0+at,加速度a=80m/s2=8g,飞行员不会昏厥,选项C错误;根据牛顿第二定律F-mg-f=ma,推力F=mg+f+ma=1.84×106N,选项B正确;加速阶段上升的高度x=v0t+at2=4500m,即匀速上升距离14km,选项D错误;匀速飞行时间t==s=16.47s,选项A错误。
6.(2018·江苏常州田家炳中学调研)如图所示,小车上固定一水平横杆,横杆左端的固定斜杆与竖直方向成α角,斜杆下端连接一质量为m的小球;横杆右端用一根细线悬挂相同的小球。当小车沿水平面做匀加速直线运动时,细线与竖直方向间的夹角β(β≠α)保持不变。设斜杆、细线对小球的作用力分别为F1、F2,下列说法正确的是( BD )
A.F1、F2可能相同
B.F1、F2一定相同
C.小车加速度大小为gtanα
D.小车加速度大小为gtanβ
[解析] 以右边的小球为研究对象,根据牛顿第二定律,设其质量为m,有mgtanβ=ma,得a=gtanβ;以左边的小球为研究对象,设其加速度为a′,斜杆对小球的弹力方向与竖直方向夹角为θ,由牛顿第二定律得mgtanθ=ma′;因为a=a′,得θ=β,则斜杆对小球的弹力方向与细线平行,即F1、F2
方向相同,大小相等,故A错误,B正确;小车的加速度大小为a=gtanβ,方向向右,故D正确,C错误。
7.(2018·广东佛山一模)如图甲所示,物体置于一固定的斜面上,与斜面间的动摩擦因数为μ。对物体施加水平向右、大小变化的外力F,保持物体沿斜面向下做加速运动,加速度a随外力F变化的关系如图乙所示。物体不脱离斜面的条件是F≤20N,若重力加速度g取10m/s2,最大静摩擦力等于滑动摩擦力,根据图乙中所提供的信息,经过分析计算可以求出( ABD )
A.物体的质量
B.斜面倾角的正弦值
C.物体运动6s时经过的位移
D.加速度为6m/s2时物体对斜面的压力
[解析] 对物体受力分析如图所示,
设斜面的倾角为θ,当F=0时,可知a1=2m/s2,则mgsinθ-μmgcosθ=ma1;当F=20N时,Fcosθ+mgsinθ=ma2,a2=m/s2,此时Ff=0,Fsinθ=mgcosθ,sin2θ+cos2θ=1,联立可得μ=,m=kg,sinθ=,故A、B正确;由于物体的初速度及F随时间的变化情况未知,因此无法求解物体运动6s时经过的位移,故C错误;当a=6m/s2时,可求得F=N,由FN+Fsinθ=mgcosθ,物体所受的支持力FN=N,则物体对斜面的压力FN′=N,故D正确。
8.(2018·河南洛阳一模)如图所示,某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向的夹角α=60°,使飞行器恰好沿与水平方向的夹角θ=30°的直线斜向右上方匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速直线飞行,飞行器所受空气阻力不计。下列说法中正确的是( BC )
A.飞行器加速时动力的大小等于mg
B.飞行器加速时加速度的大小为g
C.飞行器减速时动力的大小等于mg
D.飞行器减速飞行时间t后速度为零
[解析] 飞行器恰好沿与水平方向的夹角θ=30°的直线斜向右上方匀加速飞行时,受力分析图如图甲所示,由几何关系知2mgcos30°=F,可得加速时动力的大小等于F=mg,选项A错误;动力F与飞行器的重力mg的合力大小等于mg,所以飞行器加速时加速度的大小为g,选项B正确;飞行器沿原方向匀减速飞行时,受力分析图如图乙所示,由几何关系知sin60°=,可得飞行器减速时动力的大小等于F′=mg,选项C正确;飞行器加速飞行时间t后的速度为v=at=gt,减速飞行时合外力大小为mgcos60°=,则减速飞行时加速度大小为,减速飞行时间2t后速度为零,选项D错误。
二、非选择题
9.(2019·湖南师大附中高三月考)2018年2月在平昌冬奥会中,我国运动员李馨参加了两项越野滑雪的比赛,成绩有重大突破。如图所示,某次滑雪训练中,如果该运动员站在水平雪道上第一次利用滑雪杖对雪面的作用获得水平推力F=102N,由静止向前滑行,其作用时间为t1=1.0s,撤除水平推力F后经过t2=2.0s,运动员第二次利用滑雪杖对雪面的作用获得同样的水平推力,作用距离与第一次相同。已知该运动员连同装备(可视为质点)的总质量为m=60kg,在整个运动过程中受到的滑动摩擦力大小恒为Ff=12N,求:
(1)运动员第一次利用滑雪杖对雪面作用结束时获得的速度和3s时的速度;
(2)该运动员第二次撤除水平推力后能滑行的最大距离。
[答案] (1)1.5m/s,1.1m/s (2)8.65m
[解析] (1)运动员利用滑雪杖获得的加速度为a1==1.5m/s2
第一次利用滑雪杖对雪面作用获得速度v1=a1t1=1.5×1.0m/s=1.5m/s
运动员停止使用滑雪杖后,加速度大小为a2==0.2m/s2
经时间t2速度变为v2=v1-a2t2=1.1m/s
(2)第二次利用滑雪杖获得的速度大小为v3,则v-v=v
第二次撤除水平推力后滑行的最大距离x2==8.65m
10.(2019·浙江协作校联考)如图甲所示是高层建筑配备的救生缓降器材,由调速器、安全带、安全钩、缓降绳索等组成。发生火灾时,使用者先将安全钩挂在室内窗户、管道等可以承重的物体上,然后将安全带系在人体腰部,通过缓降绳索等安全着陆。如图乙所示,是某中学在某次火灾逃生演练现场中,体重为60kg的逃生者从离地面18m高处,利用缓降器材由静止开始匀加速下滑,当速度达到6m/s时,以大小为2.5m/s2加速度减速,到达地面时速度恰好为零。假设逃生者下降过程中悬空不接触墙面,不计空气阻力(g=10m/s2),求:
(1)减速下滑过程的位移;
(2)减速下滑时逃生者对缓降绳索的拉力大小;
(3)到达地面整个过程的时间。
[答案] (1)7.2m (2)750N (3)6.0s
[解析] (1)由题意可知减速过程:
由v2=2a1x,
有x1=7.2m
(2)减速过程
F-mg=ma1
得F=750N
根据牛顿第三定律,逃生者对缓降绳索的拉力大小750N
(3)加速过程时间t2==3.6s
减速过程时间t1==2.4s
t总=t1+t2=6.0s
11.(2018·湖南长郡中学月考)如图所示,在倾角θ=37°的足够长的固定斜面上,有一质量m=1kg的物体,物体与斜面间动摩擦因数μ=0.2。物体受到平行于斜面向上的轻细线的拉力F=9.6N的作用,从静止开始运动,经2s绳子突然断了。则绳断后经过多长时间物体的速度大小为22m/s?(结果保留两位有效数字,已知sin37°=0.6,g取10m/s2)
[答案] 5.5s
[解析] 第一阶段:在前2s内,物体在F=9.6N的拉力作用下,从静止开始沿斜面做匀加速运动,设加速度为a1,
沿斜面方向:F-mgsinθ-Ff=ma1
垂直于斜面方向:FN=mgcosθ
Ff=μFN
联立解得a1==2m/s2
2s末绳断时,物体的瞬时速度v1=a1t1=4m/s
第二阶段:从绳断到物体继续沿斜面向上运动到速度为零的过程,设加速度为a2,则
a2==-7.6m/s2
设从绳断到物体到达最高点所需时间为t2,由运动学公式得0=v1+a2t2,得t2=0.53s
第三阶段:物体从最高点沿斜面下滑,设加速度为a3,速度达到22m/s所需时间为t3。由牛顿第二定律知
a3==4.4m/s2
所需时间t3==5s
综上所述,从绳断到物体的速度为22m/s所经历的总时间t=t2+t3=0.53s+5s≈5.5s。