- 2021-05-26 发布 |
- 37.5 KB |
- 27页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习 牛顿运动定律在直线运动中的应用课件(共27张)(全国通用)
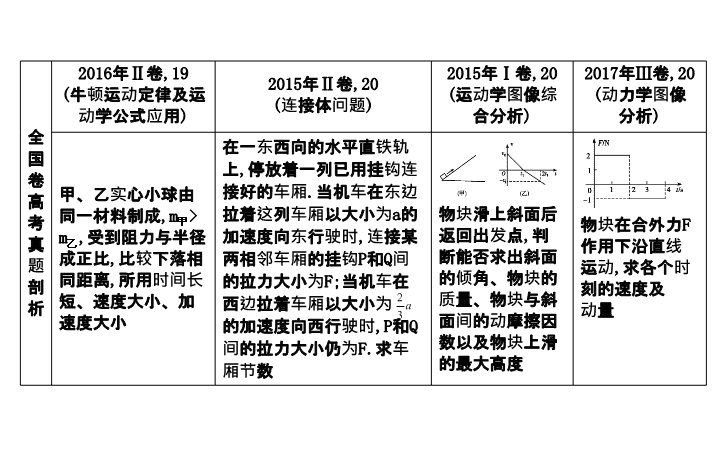
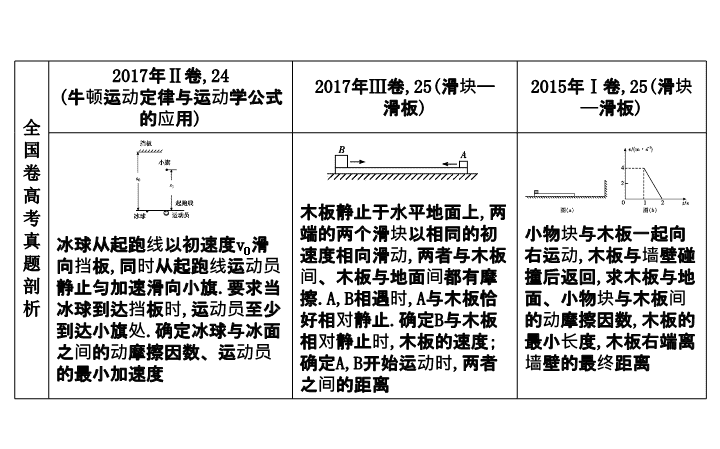
高考热点剖析 牛顿运动定律在直线运动中的应用 全国卷高考真题剖析 2016 年 Ⅱ 卷 ,19 ( 牛顿运动定律及运动学公式应用 ) 2015 年 Ⅱ 卷 ,20 ( 连接体问题 ) 2015 年 Ⅰ 卷 ,20 ( 运动学图像综合分析 ) 2017 年 Ⅲ 卷 ,20 ( 动力学图像 分析 ) 甲、乙实心小球由同一材料制成 ,m 甲 > m 乙 , 受到阻力与半径成正比 , 比较下落相同距离 , 所用时间长短、速度大小、加速度大小 在一东西向的水平直铁轨上 , 停放着一列已用挂钩连接好的车厢 . 当机车在东边拉着这列车厢以大小为 a 的加速度向东行驶时 , 连接某两相邻车厢的挂钩 P 和 Q 间的拉力大小为 F; 当机车在西边拉着车厢以大小为 的加速度向西行驶时 ,P 和 Q 间的拉力大小仍为 F. 求车厢节数 物块滑上斜面后返回出发点 , 判断能否求出斜面的倾角、物块的质量、物块与斜面间的动摩擦因数以及物块上滑的最大高度 物块在合外力 F 作用下沿直线运动 , 求各个时刻的速度及 动量 全国卷高考真题剖析 2017 年 Ⅱ 卷 ,24 ( 牛顿运动定律与运动学公式的应用 ) 2017 年 Ⅲ 卷 ,25( 滑块 — 滑板 ) 2015 年 Ⅰ 卷 ,25( 滑块 — 滑板 ) 冰球从起跑线以初速度 v 0 滑向挡板 , 同时从起跑线运动员静止匀加速滑向小旗 . 要求当冰球到达挡板时 , 运动员至少到达小旗处 . 确定冰球与冰面之间的动摩擦因数、运动员的最小加速度 木板静止于水平地面上 , 两端的两个滑块以相同的初速度相向滑动 , 两者与木板间、木板与地面间都有摩擦 .A,B 相遇时 ,A 与木板恰好相对静止 . 确定 B 与木板相对静止时 , 木板的速度 ; 确定 A,B 开始运动时 , 两者之间的距离 小物块与木板一起向右运动 , 木板与墙壁碰撞后返回 , 求木板与地面、小物块与木板间的动摩擦因数 , 木板的最小长度 , 木板右端离墙壁的最终距离 全国卷高考真题剖析 2015 年 Ⅱ 卷 ,25( 滑块 — 滑板 ) 2017 年 Ⅰ 卷 ,25 ( 牛顿运动定律及运动学公式应用 ) 2016 年 Ⅱ 卷 ,24 ( 牛顿运动定律及运动学公式在磁场中的 应用 ) 石板 B 静止在山坡 C 上 ,B 上静止一碎石堆 A. 某次暴雨中 ,A,B 间 ,B,C 间的动摩擦因数变小 ,A,B 开始运动 . 确定不同时刻 A 和 B 加速度的大小 ,A 在 B 上总的运动时间 带电油滴在 E 1 的匀强电场中竖直向上匀速运动 , 在位置 A 时 , 电场强度突然增大 , 时间 t 1 后突然反向 , 持续同样一段时间 . 确定油滴的末速度 , 确定后来的电场强度比原来的大时 t 1 和 v 0 应满足的条件 金属杆在水平向右、大小为 F 的恒定拉力作用下由静止开始运动 , 且在磁场中恰好能保持匀速运动 , 动摩擦因数为 μ, 求电动势大小及电阻阻值 技 法 提 炼 1. 牢记基本定律 : 牛顿第二定律 , 即 F 合 =ma 或 F x =ma x ,F y =ma y . 2. 熟记几种方法 , 解题畅通无阻 (1) 对图像问题 , 要多从由图线的斜率 , 图线与时间轴围成的面积的物理意义上挖掘信息 . (2) 对与系统相关的问题 , 要交叉选用整体法与隔离法 . (3) 摩擦力的分析是“传送带”“滑块 - 滑板”问题的突破点 . (4) 加速度不同是把多过程问题划分成各个分阶段的依据 , 速度是联系各个分阶段的桥梁 . 3. 几个好用的结论 , 要牢记巧用 (1) 匀减速直线运动可视为反方向的匀加速直线运动 . (2) 单棒切割磁感线时的安培力 F= . 4. 临界问题 (1) 滑块不从板上掉下来的临界条件是滑块到达滑板末端 , 且两者共速 . (2) 滑块与滑板达到共速时 , 是摩擦力发生突变的临界条件 . 常 考 类 型 1. 动力学图像的综合问题 2. 连接体问题 (1) 加速度大小相等 , 方向相同 (2) 加速度大小相等 , 方向不同 3. 牛顿运动定律与运动学公式的实际应用 4. 动力学中的临界极值问题 (1) 接触与脱离的临界问题 (2) 叠加体系统的临界极值问题 5.“ 滑块 — 滑板”模型 (1) 滑块与滑板达到共同速度后相对静止 (2) 滑块与滑板达到共同速度后相对滑动 6. 应用牛顿运动定律分析电场中的物体往复运动问题 7. 应用牛顿运动定律分析电磁感应中的物体运动问题 【 热点集训 】 1.[ 加速度方向相同的连接体 ] 如图所示,质量分别为m和2m的两个小球置于光滑水平面上,且固定在一轻质弹簧的两端,现沿弹簧轴线方向在质量为2m的小球上施加一水平向右的拉力F 1 ,使两球一起做匀加速运动,则此时两球间的距离为x 1 ,若沿弹簧轴线方向在质量为m的小球上施加一水平向左的拉力F 2 ,使两球一起做匀加速运动,则此时两球间的距离为x 2 ,已知x 1 =2x 2 ,则有( ) A.F 1 =F 2 B.F 1 =4F 2 C.F 1 >4F 2 D.F 1 =2F 2 C 2.[ 加速度方向不同的连接体 ] ( 多选 ) 如图所示 , 一根轻绳跨过定滑轮 , 两端分别系着质量为 m 1 ,m 2 的小物块 A 和 B,A 放在地面上 ,B 离地面有一定高度 . 当 B 的质量发生变化时 ,A 上升的加速度 a 和拉 A 绳的拉力 F 也将随之变化 ( 全过程 A 始终未碰到滑轮 ,B 始终未触地 ). 已知重力加速度为 g, 不计轻绳和滑轮之间的摩擦 , 则下列关于 a 与 m 2 及 T 与 m 2 关系的图像 , 描述正确的是 ( ) AC 3.[ 运动图像与动力学的综合 ]( 2017 · 吉林实验中学二模 ) 如图 ( 甲 ) 所示 , 一轻质弹簧的下端固定在水平面上 , 上端放置一物体 ( 物体与弹簧不连接 ), 初始时物体处于静止状态 . 现用竖直向上的拉力 F 作用在物体上 , 使物体开始向上做匀加速运动 , 拉力 F 与物体位移 x 之间的关系如图 ( 乙 ) 所示 (g=10 m/s 2 ), 则下列结论正确的是 ( ) A. 物体的加速度大小为 5 m/s 2 B. 弹簧的劲度系数为 7.5 N/cm C. 物体的质量为 3 kg D. 物体与弹簧分离时 , 弹簧处于压缩状态 A 解析 : 刚开始物体处于静止状态 , 重力和弹力二力平衡 , 有 mg=kx, 拉力 F 1 为 10 N 时 , 弹簧弹力和重力平衡 , 合力等于拉力 , 根据牛顿第二定律 , 有 F 1 +kx-mg=ma, 物体与弹簧分离后 , 拉力 F 2 为 30 N, 根据牛顿第二定律 , 有 F 2 -mg=ma, 联立解得 m=2 kg,k=500 N/m=5 N/cm,a=5 m/s 2 , 选项 A 正确 ,B,C 错误 ; 物体与弹簧分离时 , 弹簧恢复原长 , 选项 D 错误 . 4.[ 应用牛顿运动定律分析电场中物体的运动 ] ( 多选 ) 地面附近存在着一有界电场 , 边界 MN 将某空间分成上、下两个区域 Ⅰ,Ⅱ, 在区域 Ⅱ 中有竖直向上的匀强电场 , 在区域 Ⅰ 中离边界某一高度处由静止释放一质量为 m 的带电小球 A, 如图 ( 甲 ) 所示 , 小球运动的 v - t 图像如图 ( 乙 ) 所示 , 已知重力加速度为 g, 不计空气阻力 , 则 ( ) A. 在 t=2.5 s 时 , 小球经过边界 MN B. 小球受到的重力与电场力之比为 3∶5 C. 在小球向下运动的整个过程中 , 重力做的功与小球克服电场力做的功大小 相等 D. 在小球进入电场到再次从电场中出来过程中小球所受冲量大小为 2mv 1 BCD 5.[ 微粒在电磁场中的直线运动 ] 质量为 m 、电荷量为 q 的微粒 , 以速度 v 与水平方向成 θ 角从 O 点进入方向如图所示的正交的匀强电场 ( 电场强度大小为 E) 和匀强磁场 ( 磁感应强度大小为 B) 组成的混合场区 , 该微粒在电场力、洛伦兹力和重力的作用下 , 恰好沿直线运动到 A, 重力加速度为 g, 下列说法中正确的是 ( ) A. 该微粒一定带正电 B. 微粒从 O 到 A 的运动可能是匀变速运动 C. 该磁场的磁感应强度大小为 D. 该电场的场强为 Bvcos θ C 解析 : 若微粒带正电 , 电场力水平向左 , 洛伦兹力垂直 OA 斜向右下方 , 则电场力、重力、洛伦兹力不能平衡 ; 若微粒带负电 , 符合题意 , 选项 A 错误 ; 微粒如果做匀变速运动 , 重力和电场力不变 , 而洛伦兹力变化 , 微粒不能沿直线运动 , 与题意不符 , 选项 B 错误 ; 由平衡条件得 qvBcos θ=mg,qvBsin θ=qE, 知选项 C 正确 ,D 错误 . 6.[ 应用牛顿运动定律分析电磁感应中物体的运动 ]( 2017 · 四川成都二诊 ) ( 多选 ) 如图所示 , 两根足够长的平行金属导轨相距 L, 其中 NO 1 ,QO 2 部分水平 , 倾斜部分 MN,PQ 与水平面的夹角均为 α, 整个空间存在磁感应强度为 B 的匀强磁场 , 磁场方向垂直导轨平面 MNQP 向上 . 长为 L 的金属棒 ab,cd 与导轨垂直放置且接触良好 , 其中 ab 光滑 ,cd 粗糙 , 棒的质量均为 m 、电阻均为 R. 将 ab 由静止释放 , 在 ab 下滑至速度刚达到稳定的过程中 ,cd 始终静止不动 . 若导轨电阻不计 , 重力加速度为 g, 则在上述过程中 ( ) A.ab 棒做加速度减小的加速运动 B.ab 棒下滑的最大速度为 C.cd 棒所受摩擦力的最大值为 mgsin αcos α D.cd 棒中产生的热量等于 ab 棒机械能的减少量 AC 7.[ 临界极值问题 ]( 2017 · 海南卷 ,14 ) 一轻弹簧的一端固定在倾角为 θ 的固定光滑斜面的底部 , 另一端和质量为 m 的小物块 a 相连 , 如图所示 . 质量为 m 的小物块 b 紧靠 a 静止在斜面上 , 此时弹簧的压缩量为 x 0 , 从 t=0 时开始 , 对 b 施加沿斜面向上的外力 , 使 b 始终做匀加速直线运动 . 经过一段时间后 , 物块 a,b 分离 ; 再经过同样长的时间 ,b 距其出发点的距离恰好也为 x 0 . 弹簧的形变始终在弹性限度内 , 重力加速度大小为 g. 求 : (1) 弹簧的劲度系数 ; (2) 物块 b 加速度的大小 ; (3) 在物块 a,b 分离前 , 外力大小随时间变化的关系式 . 8.[ 滑块 — 滑板问题 ]( 2017 · 江西南昌模拟 ) 如图所示 , 在水平地面上建立 x 轴 , 有一个质量 m=1 kg 的木块放在质量为 M=2 kg 的长木板上 , 木板长 L=11.5 m. 已知木板与地面间的动摩擦因数为 μ 1 =0.1, 木块与长木板之间的动摩擦因数为 μ 2 =0.9( 设最大静摩擦力等于滑动摩擦力 ). 木块与长木板保持相对静止共同向右运动 , 已知木板的左端 A 点经过坐标原点 O 时的速度为 v 0 =10 m/s, 在坐标为 x=21 m 处的 P 点处有一挡板 , 木板与挡板瞬间碰撞后立即以原速率反向弹回 , 而木块在此瞬间速度不变 , 若碰后立刻撤去挡板 ,g 取 10 m/s 2 . 求 : (1) 木板碰挡板时的速度大小 v 1 ; 答案 : (1)9 m/s (2) 碰后木板与木块刚好共速时的速度 ; 答案 : (2)1.8 m/s 方向向左 (3) 最终木板停止运动时 A,P 间的距离 . 答案 : (3)19.60 m 谢谢观赏!查看更多