【物理】2020届一轮复习人教版专题十确定带电粒子在磁场中运动轨迹的方法学案

【物理】2020届一轮复习人教版专题十确定带电粒子在磁场中运动轨迹的方法学案

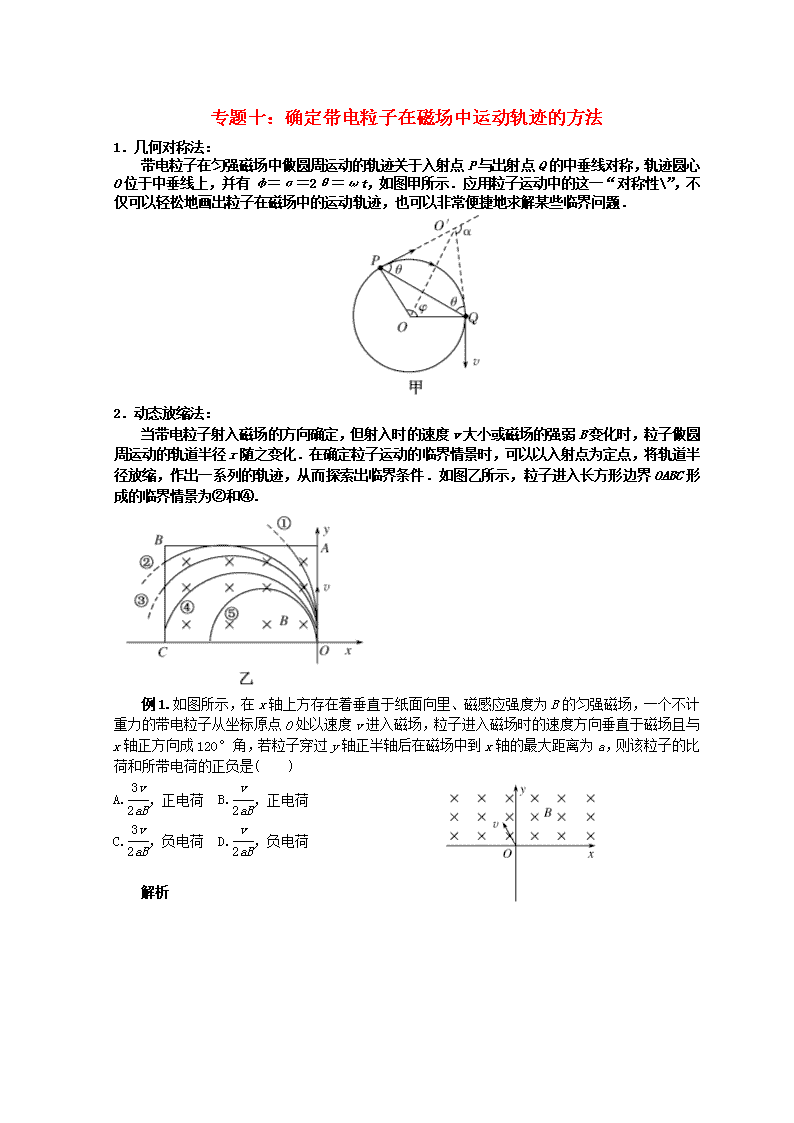
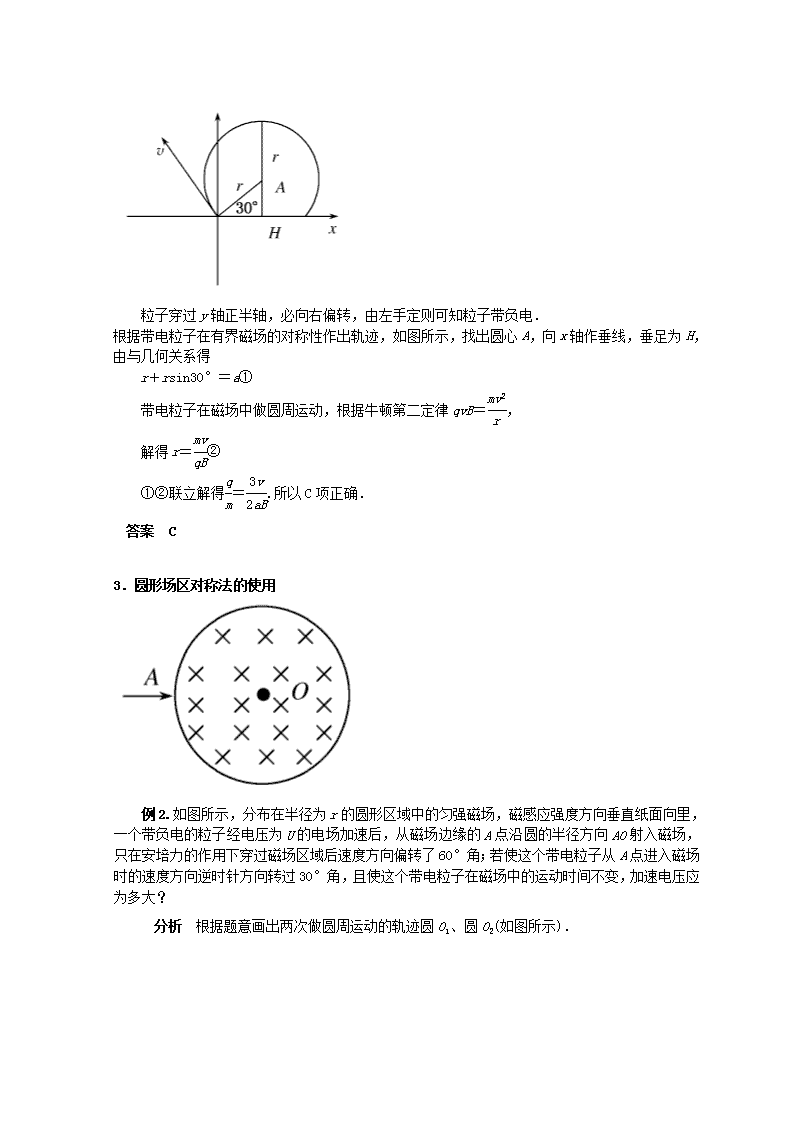
专题十：确定带电粒子在磁场中运动轨迹的方法 ‎1．几何对称法：‎ 带电粒子在匀强磁场中做圆周运动的轨迹关于入射点P与出射点Q的中垂线对称，轨迹圆心O位于中垂线上，并有φ＝α＝2θ＝ωt，如图甲所示．应用粒子运动中的这一“对称性”，不仅可以轻松地画出粒子在磁场中的运动轨迹，也可以非常便捷地求解某些临界问题．‎ ‎2．动态放缩法：‎ 当带电粒子射入磁场的方向确定，但射入时的速度v大小或磁场的强弱B变化时，粒子做圆周运动的轨道半径r随之变化．在确定粒子运动的临界情景时，可以以入射点为定点，将轨道半径放缩，作出一系列的轨迹，从而探索出临界条件．如图乙所示，粒子进入长方形边界OABC形成的临界情景为②和④.‎ 例1.如图所示，在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场，一个不计重力的带电粒子从坐标原点O处以速度v进入磁场，粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成120°角，若粒子穿过y轴正半轴后在磁场中到x轴的最大距离为a，则该粒子的比荷和所带电荷的正负是(　　)‎ A.，正电荷 B.，正电荷 C.，负电荷 D.，负电荷 解析　‎ 粒子穿过y轴正半轴，必向右偏转，由左手定则可知粒子带负电．‎ 根据带电粒子在有界磁场的对称性作出轨迹，如图所示，找出圆心A，向x轴作垂线，垂足为H，由与几何关系得 r＋rsin30°＝a①‎ 带电粒子在磁场中做圆周运动，根据牛顿第二定律qvB＝，‎ 解得r＝②‎ ‎①②联立解得＝.所以C项正确．‎ 答案　C ‎3．圆形场区对称法的使用 例2.如图所示，分布在半径为r的圆形区域中的匀强磁场，磁感应强度方向垂直纸面向里，一个带负电的粒子经电压为U的电场加速后，从磁场边缘的A点沿圆的半径方向AO射入磁场，只在安培力的作用下穿过磁场区域后速度方向偏转了60°角；若使这个带电粒子从A点进入磁场时的速度方向逆时针方向转过30°角，且使这个带电粒子在磁场中的运动时间不变，加速电压应为多大？‎ 分析　根据题意画出两次做圆周运动的轨迹圆O1、圆O2(如图所示)．‎ 解析　设带电粒子质量为m、电荷量为q.‎ 沿AO射入：‎ 设圆周运动半径为R1，‎ 速度方向偏离入射方向60°角，则圆心角∠AO1K＝60°，所以R1＝r；‎ 逆时针方向转过30°角入射：‎ 设圆周运动半径为R2、加速电压为U2.‎ 因为在磁场中运动时间不变，根据t＝T可知，两次的圆心角相等，则∠AO2D＝60°，所以R2＝2r.‎ 根据半径公式R＝和加速过程Uq＝mv2得U2＝U1＝U.‎ 答案　U 规律总结　‎ 在这类题中注意圆的对称性，如果沿径向入射，则必沿径向出射；轨迹圆和圆域都关于两圆心对称，即两圆心连线把两个圆平分．‎ ‎4．定圆旋转法：当带电粒子射入磁场时的速率v大小一定，但射入的方向变化时，粒子做圆周运动的轨道半径r是确定的．在确定粒子运动的临界情景时，可以以入射点为定点，将轨迹圆旋转，作出一系列轨迹，从而探索出临界条件，如图丙所示为粒子进入单边界磁场时的情景．‎ ‎5．数学解析法：写出轨迹圆和边界的解析方程，应用物理和数学知识求解．‎ 例3.如图所示，在一水平放置的平板MN的上方有匀强磁场，磁感应强度的大小为B，磁场方向垂直于纸面向里．许多质量为m带电荷量为＋q的粒子，以相同的速率v沿位于纸面内的各个方向，由小孔O射入磁场区域．不计重力，不计粒子间的相互影响．下列图中阴影部分表示带电粒子可能经过的区域，其中哪个图是正确的(　　)‎ 解析　带电粒子垂直进入匀强磁场中，将做圆周运动．‎ 由于它们入射速度大小相等，所做圆周运动的半径相等，向垂直于磁场的各个方向发射粒子，所以粒子的运动轨迹是围绕发射点以2R为半径旋转的动态圆，多画几个不同方向粒子运动的轨迹，尤其一些典型和特殊的，通过观察可得出所有这些圆周所覆盖的区域，即为所求，‎ 如图所示．‎ 区域的边缘，左边以O为圆心以2R为半径的圆，右边则是从O点几乎沿MN方向射入的粒子的轨迹．‎ 答案　A