【物理】2018届二轮　功能关系和能量守恒专题卷（全国通用）

【物理】2018届二轮　功能关系和能量守恒专题卷（全国通用）

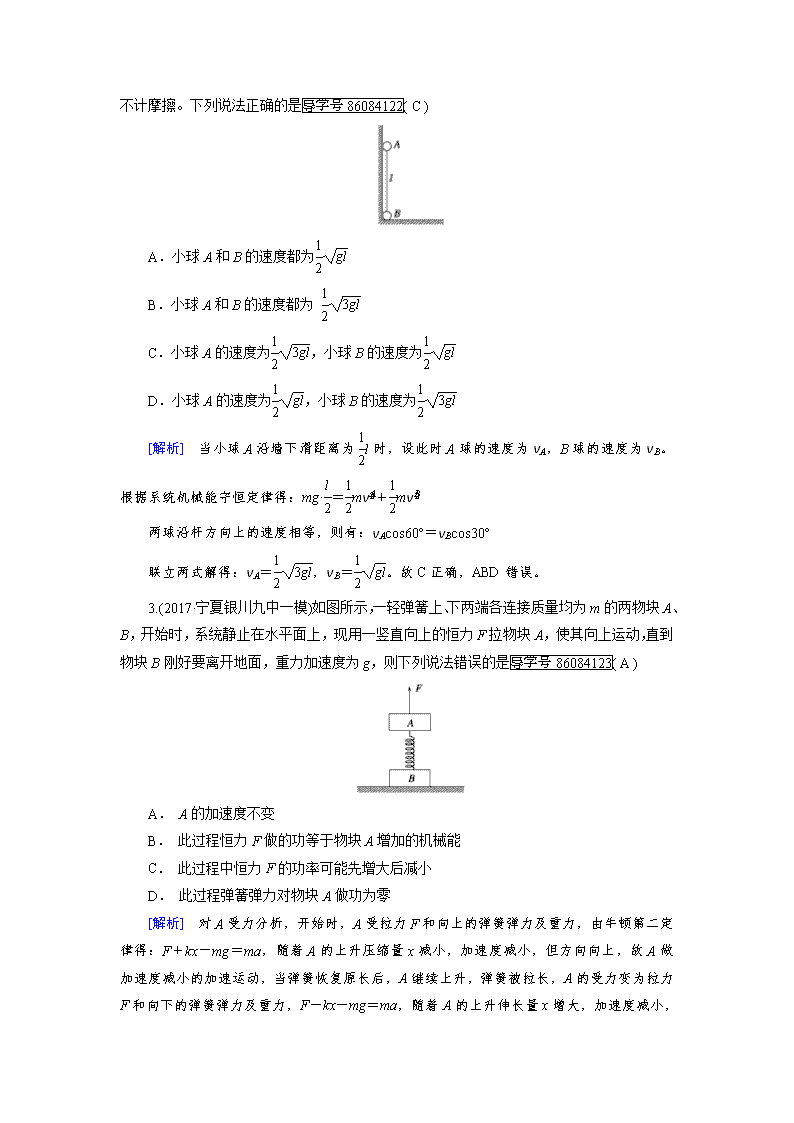
专题二　第6讲 限时：40分钟 一、选择题(本题共8小题，其中1～4题为单选，5～8题为多选)‎ ‎1．(2017·山东省潍坊一模)如图所示，在竖直面内固定一光滑的硬质杆ab，杆与水平面的夹角为θ，在杆的上端a处套一质量为m的圆环，圆环上系一轻弹簧，弹簧的另一端固定在与a处在同一水平线上的O点，O、b两点处在同一竖直线上。由静止释放圆环后，圆环沿杆从a运动到b，在圆环运动的整个过程中，弹簧一直处于伸长状态，则下列说法正确的是( D )‎ A． 圆环的机械能保持不变 B． 弹簧对圆环一直做负功 C． 弹簧的弹性势能逐渐增大 D． 圆环和弹簧组成的系统机械能守恒 ‎[解析]　由几何关系可知，当环与O点的连线与杆垂直时，弹簧的长度最短，弹簧的弹性势能最小。所以在环从a到C的过程中弹簧对环做正功，而从C到b的过程中弹簧对环做负功，所以环的机械能是变化的。故A错误，B错误；‎ 当环与O点的连线与杆垂直时，弹簧的长度最短，弹簧的弹性势能最小，所以弹簧的弹性势能先减小后增大。故C错误；在整个的过程中只有重力和弹簧的弹力做功，所以圆环和弹簧组成的系统机械能守恒。故D正确；故选D。‎ ‎2. (2017·广东省肇庆市二模)如图所示，一个长直轻杆两端分别固定一个小球A和B，两球质量均为m，两球半径忽略不计，杆的长度为l。先将杆AB竖直靠放在竖直墙上，轻轻振动小球B，使小球B在水平面上由静止开始向右滑动，当小球A沿墙下滑距离为l 时，不计摩擦。下列说法正确的是( C )‎ A．小球A和B的速度都为 B．小球A和B的速度都为 C．小球A的速度为，小球B的速度为 D．小球A的速度为，小球B的速度为 ‎[解析]　当小球A沿墙下滑距离为l时，设此时A球的速度为vA，B球的速度为vB。根据系统机械能守恒定律得：mg·＝mv＋mv 两球沿杆方向上的速度相等，则有：vAcos60°＝vBcos30°‎ 联立两式解得：vA＝，vB＝。故C正确，ABD错误。‎ ‎3.(2017·宁夏银川九中一模)如图所示，一轻弹簧上、下两端各连接质量均为m的两物块A、B，开始时，系统静止在水平面上，现用一竖直向上的恒力F拉物块A，使其向上运动，直到物块B刚好要离开地面，重力加速度为g，则下列说法错误的是( A )‎ A． A的加速度不变 B． 此过程恒力F做的功等于物块A增加的机械能 C． 此过程中恒力F的功率可能先增大后减小 D． 此过程弹簧弹力对物块A做功为零 ‎[解析]　对A受力分析，开始时，A受拉力F和向上的弹簧弹力及重力，由牛顿第二定律得：F＋kx－mg＝ma，随着A的上升压缩量x减小，加速度减小，但方向向上，故A做加速度减小的加速运动，当弹簧恢复原长后，A继续上升，弹簧被拉长，A的受力变为拉力F和向下的弹簧弹力及重力，F－kx－mg＝ma，随着A的上升伸长量x增大，加速度减小，但方向向上，故A继续做加速度减小的加速运动，当弹簧伸长量最大时，B 刚好离开地面，此过程中，A的加速度是变化的，A错误；根据能量守恒可知，恒力F做的功等于物块A增加的重力势能和弹簧弹性势能的增量，而弹性势能不变，故恒力F做的功等于物块A增加的重力势能，B正确；由A项中分析可知，A先做加速再做减速运动，而力恒定，故此过程中恒力F的功率先增大后减小，C正确；由牛顿第二定律可知，开始弹簧压缩量为：x＝，最后弹簧伸长量也为：x＝，故整个过程中弹簧对A做功为零，D正确。‎ ‎4．(2017·河南省商丘市二模)正方体空心框架ABCD－A1B1C1D1下表面在水平地面上，将可视为质点的小球从顶点A在∠BAD所在范围内(包括边界)沿不同的水平方向分别抛出，落点都在△B1C1D1平面内(包括边界)。不计空气阻力，以地面为重力势能参考平面。则下列说法正确的是( D )‎ A．小球初速度的最小值与最大值之比是1： B．落在C1点的小球，运动时间最长 C．落在B1D1线段上的小球，落地时机械能的最小值与最大值之比是1：2‎ D．轨迹与AC1线段相交的小球，在交点处的速度方向都相同 ‎[解析]　小球落在A1C1线段中点时水平位移最小，落在C1时水平位移最大，由几何关系知水平位移的最小值与最大值之比是12，由x＝v0t，t相等得小球初速度的最小值与最大值之比是12，故A错误；小球做平抛运动，由h＝gt2得 t＝，下落高度相同，平抛运动的时间相等，故B错误；落在B1D1线段中点的小球，落地时机械能最小，落在B1D1线段上D1或B1的小球，落地时机械能最大。设落在B1D1线段中点的小球初速度为v1，水平位移为x1。落在B1D1线段上D1或B1的小球初速度为v2，水平位移为x2。由几何关系有 x1x2＝1，由x＝v0t，得：v1v2＝1，落地时机械能等于抛出时的机械能，分别为：E1＝mgh＋mv，E2＝mgh＋mv，可知落地时机械能的最小值与最大值之比不等于12。故C错误；设AC1的倾角为α，轨迹与AC1线段相交的小球，在交点处的速度方向与水平方向的夹角为θ。则有tanα＝＝，tanθ＝，则tanθ＝2tanα，可知θ一定，则轨迹与AC1线段相交的小球，在交点处的速度方向相同，故D正确。‎ ‎5．(2017·山东省日照市二模)如图所示，轻弹簧的一端固定在墙上，另一端与一物块相连，物块与水平面间的动摩擦因数为μ。开始时用力推着物块使弹簧压缩，将物块从A 处由静止释放，经过B处时速度最大，到达C处速度为零，AC＝L。在C处给物块一初速度，物块恰能回到A处。弹簧始终处于弹性限度内，重力加速度为g。则物块( BD )‎ A．在B处弹簧可能恢复原长 B．在C处的初速度大小一定是2 C．从C到A的运动过程中，也是在B处的速度最大 D．从C到A经过B处的速度大于从A到C经过B处的速度 ‎[解析]　物块从A到C的过程中，弹簧的弹力先大于滑动摩擦力，后小于滑动摩擦力，物块先加速后减速，所以当弹力等于滑动摩擦力时速度最大，此时弹簧处于压缩状态。故A错误；设释放前弹簧的弹性势能为Ep。根据能量守恒定律得从A→C的过程有：Ep＝μmgL , 从C→A的过程有：Ep＋μmgL＝mv解得，在C处的初速度v0＝2，故B正确；从C到A的运动过程中，物块经过B时弹力向右，滑动摩擦力也向右，合力不为零，所以B点的速度不是最大，故C错误；两次经过B点时弹簧的弹性势能相同，设为EpB。BC间的距离为S。根据能量守恒定律得 从B→C的过程有：EpB＋mv ＝μmgS，即得mv＝μmgS－EpB 从C→B的过程有：EpB＋μmgS＋mv2B2＝mv，即得mv2B2＝mv－EpB－μmgS 将Ep＝μmgL和Ep＋μmgL＝mv代入上式得 mv2B2 ＝2μmgL－EpB－μmgS＞mv 可知，vB2＞vB1。即从C到A经过B处的速度大于从A到C经过B处的速度。故D正确。‎ ‎6．(2017·四川省达州市一模)如图所示，质量为m的一辆小汽车从水平地面AC上的A点沿斜坡匀速行驶到B点。B距水平面高度为h，以水平地面为零势能面，重力加速度为g。小汽车从A点运动到B点的过程中(空气阻力不能忽略)，下列说法正确的是( AC )‎ A．合外力做功为零 B．合外力做功为mgh C．小汽车的机械能增加量为mgh D．牵引力做功为mgh ‎[解析]　汽车匀速运动，动能不变，则根据动能定理可知，合外力做功为零，故A正确，B错误；小汽车动能不变，重力势能增加了mgh，则可知小汽车机械能增加量为mgh，故C正确；对上升过程由动能定理可知，牵引力的功等于重力势能的增加量和克服阻力做功之和，故牵引力做功一定大于mgh，故D错误。故选：AC。‎ ‎7. (2017·山西省一模)如图所示，轻弹簧一端固定在O点，另一端与质量为m的带孔小球相连，小球套在竖直固定杆上，轻弹簧自然长度正好等于O点到固定杆的距离OO′。小球从杆上的A点由静止释放后，经过B点时速度最大，运动到C点时速度减为零。若在C点给小球一个竖直向上的初速度v，小球恰好能到达A点。整个运动过程中弹簧始终在弹性限度内，下列说法正确的是( AC )‎ A． 从A下滑到O′的过程中，弹簧弹力做功的功率先增大后减小 B． 从A下滑到C的过程中，在B点时小球、弹簧及地球组成的系统机械能最大 C． 从A下滑到C的过程中，小球克服摩擦力做的功为mv2‎ D． 从C上升到A的过程中，小球经过B点时的加速度为0‎ ‎[解析]　小球从A下滑到O′的过程，弹力与运动方向成锐角，弹力做正功，但弹力在减小，速度在增大，而在O′点弹力为零，功率为零，则整个过程弹力的功率先增大后减小，A正确；由全过程的运动可知一直有摩擦力做负功，系统的机械能一直减小，故初位置A的机械能最大，而B点仅动能最大，B错误；从A到C由动能定理：WG－Wf－WFk＝0－0，从C到A，由于路径相同和初末位置相同，则WG、Wf、WFk的大小相同，有－WG－Wf＋WFk＝0－mv2，解得Wf＝mv2，C正确；物体从A至C经过B时速度最大可知加速度为零，此时摩擦力向上与弹簧弹力、杆的弹力、重力的合力为零；而从C至A运动时同位置B的弹簧弹力和重力均相同，但摩擦力向下，故合力不为零，D错误。故选AC。‎ ‎8．(2017·湖北省襄阳五中一模)将质量为2 m的长木板静止地放在光滑水平面上，如图甲所示。第一次，质量为m的小铅块(可视为质点)，在木板上以水平初速度v0‎ 由木板左端向右运动恰能滑至木板的右端与木板相对静止。第二次，将木板分成长度与质量均相等的两段1和2，两者紧挨着仍放在此水平面上，让小铅块以相同的初速度v0由木板1的左端开始滑动，如图乙所示．设铅块与长木板间的动摩擦因数为μ，重力加速度为g，对上述两过程，下列判断正确的是( BD )‎ A．铅块在木板1上滑动时两段木板间的作用力为μmg B．铅块在木板1上滑动时两段木板间的作用力为μmg C．小铅块第二次仍能到达木板2的右端 D．系统第一次因摩擦而产生的热量较多 ‎[解析]　第二次小铅块先使整个木板加速，根据牛顿第二定律得a＝＝μg，对2木板根据牛顿第二定律得：F12＝ma＝μmg，故A错误，B正确；在第一次小铅块运动过程中，小铅块与木板之间的摩擦力使整个木板一直加速，第二次小铅块先使整个木板加速，运动到2部分上后1部分停止加速，只有2部分加速，加速度大于第一次的对应过程，故第二次小铅块与2木板将更早达到速度相等，所以小铅块还没有运动到2的右端，故C错误；由于在乙中小铅块还没有运动到2的右端，所以在木板2上相对运动的位移没有在木板1上大，所以在乙中小铅块相对木板的位移小于在甲中小铅块相对木板的位移，根据摩擦力乘以相对位移等于产生的热量，所以乙中产生的热量小于在甲中木板上滑行产生热量，故D正确。‎ 二、计算题(本题共2小题，需写出完整的解题步骤)‎ ‎9. (2017·江西省师大附中一模)如图所示，A、B质量分别为mA＝1 kg，mB＝2 kg，AB间用弹簧连接着，弹簧劲率系数k＝100 N/m，轻绳一端系在A上，另一端跨过定滑轮，B为套在轻绳上的光滑圆环，另一圆环C固定在桌边，B被C挡住而静止在C上，若开始时作用在绳子另一端的拉力F为零，此时A处于静止且刚没接触地面。现用恒定拉力F＝15 N拉绳子，恰能使B离开C但不能继续上升，不计摩擦且弹簧没超过弹性限度，g＝10 m/s2求： ‎(1)B刚要离开C时A的加速度；‎ ‎(2)若把拉力F改为F′＝30N，则B刚要离开C时，A的速度大小。‎ ‎[解析]　(1)B刚要离开C的时候，弹簧对B的弹力N＝mBg：‎ 对A有：aA＝＝15 m/s2‎ ‎(2)当F＝0时，弹簧的伸长量x1＝mAg/k＝0.1 m 当F＝15 N，且A上升到最高点时，弹簧的压缩量x2＝mBg/k＝0.2 m 所以A上升的高度h＝x1＋x2＝0.3 m A上升过程中：Fh＝mAgh＋ΔEp所以弹簧弹性势能增加了ΔEp＝1.5 J 把拉力改为F′＝30 N时，A上升过程中：‎ F′h－mAgh－ΔEp＝mAv2　得v＝3 m/s ‎10．(2017·山东省历城二中二模) 如图所示，半径为R、圆心为O的大圆环固定在竖直平面内，两个轻质小圆环固定在大圆环上竖直对称轴的两侧θ＝45°的位置上，一根轻质长绳穿过两个小圆环，它的两端都系上质量为m的重物，小圆环的大小、绳子与大、小圆环间的摩擦均可 忽略。当在两个小圆环间绳子的中点C处，挂上一个质量M的重物，M恰好在圆心处处于平衡。(重力加速度为g)求： ‎(1)M与m质量之比。‎ ‎(2)再将重物M托到绳子的水平中点C处，然后无初速释放重物M，则重物M到达圆心处的速度是多大？‎ ‎[解析]　(1)以M为研究对象，受力分析：Mg＝2mgcos45°‎ ＝ ‎(2)M与2个m组成的系统机械能守恒：‎ MgRsinθ－2mg(R－Rcosθ)＝Mv＋2×mv v2＝v1cosθ 　v1＝(－1)