【物理】2018届一轮复习教科版实验十四探究单摆的运动、用单摆测定重力加速度教案

【物理】2018届一轮复习教科版实验十四探究单摆的运动、用单摆测定重力加速度教案

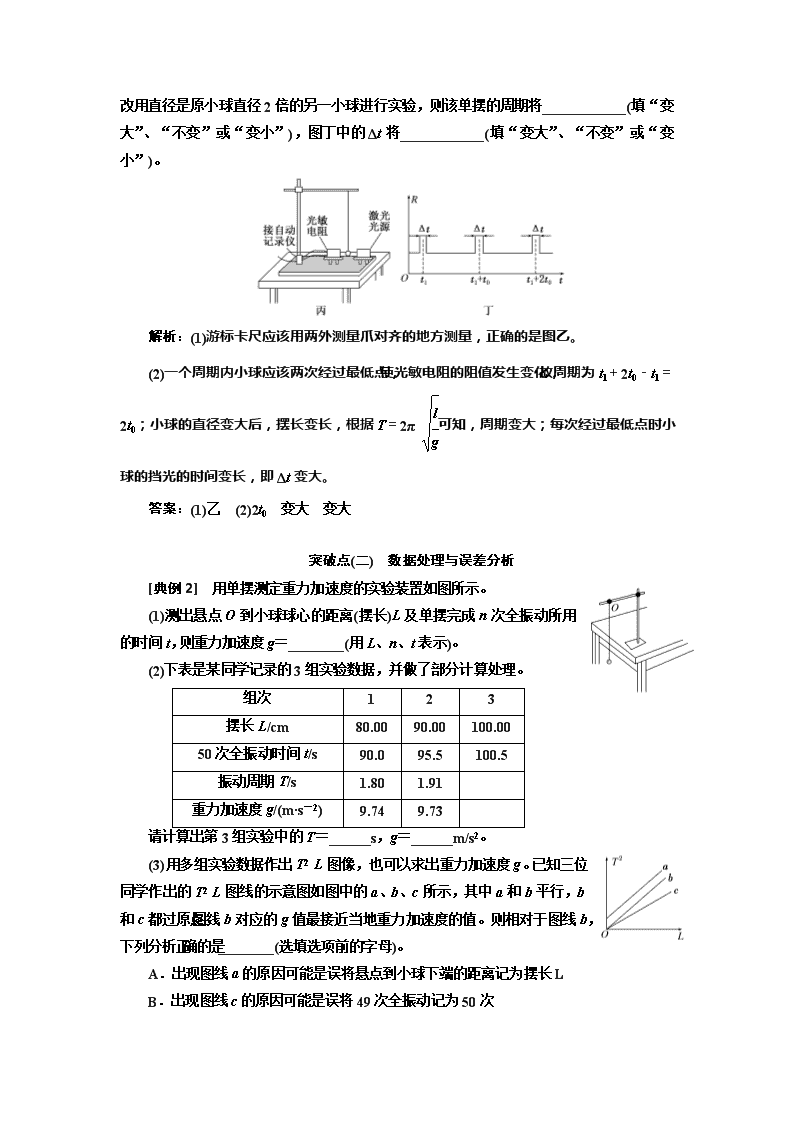
实 验 十 四 探究单摆的运动、用单摆测定重力加速度 突破点(一)　实验原理与操作 ‎[典例1]　(2013·安徽高考)根据单摆周期公式T＝2π ，可以通过实验测量当地的重力加速度。如图甲所示，将细线的上端固定在铁架台上，下端系一小钢球，就做成了单摆。‎ ‎(1)用游标卡尺测量小钢球直径，示数如图乙所示，读数为________mm。‎ ‎(2)以下是实验过程中的一些做法，其中正确的有________。‎ a．摆线要选择细些的、伸缩性小些的，并且尽可能长一些 b．摆球尽量选择质量大些、体积小些的 c．为了使摆的周期大一些，以方便测量，开始时拉开摆球，使摆线相距平衡位置有较大的角度 d．拉开摆球，使摆线偏离平衡位置不大于5°，在释放摆球的同时开始计时，当摆球回到开始位置时停止计时，此时间间隔Δt即为单摆周期T e．拉开摆球，使摆线偏离平衡位置不大于5°，释放摆球，当摆球振动稳定后，从平衡位置开始计时，记下摆球做50次全振动所用的时间Δt，则单摆周期T＝ ‎[解析]　(1)该游标尺为十分度的，根据读数规则可读出小钢球直径为‎18 mm＋6×‎0.1 mm＝‎18.6 mm。‎ ‎(2)根据用单摆测量重力加速度的实验要求可判断a、b、e正确。‎ ‎[答案]　(1)18.6　(2)abe ‎[集训冲关]‎ ‎1．用单摆测定重力加速度的实验中：‎ ‎(1)应选用下列器材中的________。‎ A．半径为‎1 cm的木球　　　　B．半径为‎1 cm的实心钢球 C．‎1 m左右的细线 D．‎30 cm左右的细线 E．秒表、三角板、米尺 ‎(2)若在某次实验中，测得细线的长度为l，摆球直径为D，单摆完成N次全振动的时间为t，则利用上述测量量求重力加速度g的表达式为________。‎ 解析：(1)为了尽量减小空气阻力对单摆的影响，要选用实心钢球；‎1 m左右的细线组成的单摆周期大约是2 s，便于计时；秒表用来计时，三角板、米尺用于测量摆长。‎ ‎(2)T＝＝2π ，解得g＝。‎ 答案：(1)BCE　(2) ‎2．(2017·金华质检)(1)在“探究单摆周期与摆长的关系”实验中，两位同学用游标卡尺测量小球的直径的操作如图甲、乙所示。测量方法正确的是________(选填“甲”或“乙”)。‎ ‎(2)实验时，若摆球在垂直纸面的平面内摆动，为了将人工记录振动次数改为自动记录振动次数，在摆球运动的最低点的左、右两侧分别放置一激光光源与光敏电阻，如图丙所示。光敏电阻与某一自动记录仪相连，该仪器显示的光敏电阻阻值R随时间t的变化图线如图丁所示，则该单摆的振动周期为____________。若保持悬点到小球顶点的绳长不变，改用直径是原小球直径2倍的另一小球进行实验，则该单摆的周期将____________(填“变大”、“不变”或“变小”)，图丁中的Δt将____________(填“变大”、“不变”或“变小”)。‎ 解析：(1)游标卡尺应该用两外测量爪对齐的地方测量，正确的是图乙。‎ ‎(2)一个周期内小球应该两次经过最低点，使光敏电阻的阻值发生变化，故周期为t1＋2t0－t1＝2t0；小球的直径变大后，摆长变长，根据T＝2π 可知，周期变大；每次经过最低点时小球的挡光的时间变长，即Δt变大。‎ 答案：(1)乙　(2)2t0　变大　变大 突破点(二)　数据处理与误差分析 ‎[典例2]　用单摆测定重力加速度的实验装置如图所示。‎ ‎(1)测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t，则重力加速度g＝________(用L、n、t表示)。‎ ‎(2)下表是某同学记录的3组实验数据，并做了部分计算处理。‎ 组次 ‎1‎ ‎2‎ ‎3‎ 摆长L/cm ‎80.00‎ ‎90.00‎ ‎100.00‎ ‎50次全振动时间t/s ‎90.0‎ ‎95.5‎ ‎100.5‎ 振动周期T/s ‎1.80‎ ‎1.91‎ 重力加速度g/(m·s－2)‎ ‎9.74‎ ‎9.73‎ 请计算出第3组实验中的T＝______s，g＝______m/s2。‎ ‎(3)用多组实验数据作出T2L图像，也可以求出重力加速度g。已知三位同学作出的T2L图线的示意图如图中的a、b、c所示，其中a和b平行，b和c都过原点，图线b对应的g值最接近当地重力加速度的值。则相对于图线b，下列分析正确的是________(选填选项前的字母)。‎ A．出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L B．出现图线c的原因可能是误将49次全振动记为50次 C．图线c对应的g值小于图线b对应的g值 ‎(4)某同学在家里测重力加速度。他找到细线和铁锁，制成一个单摆，如图所示，由于家里只有一根量程为0～‎30 cm的刻度尺，于是他在细线上的A点做了一个标记，使得悬点O到A点间的细线长度小于刻度尺量程。保持该标记以下的细线长度不变，通过改变O、A 间细线长度以改变摆长。实验中，当O、A间细线的长度分别为l1、l2时，测得相应单摆的周期为T1、T2。由此可得重力加速度g＝________(用l1、l2、T1、T2表示)。‎ ‎[解析]　(1)单摆的振动周期T＝。‎ 根据T＝2π，得g＝＝。‎ ‎(2)T3＝＝2.01 s。‎ 根据T＝2π ，得g＝≈‎9.76 m/s2。‎ ‎(3)根据T＝2π ，得T2＝L，即当L＝0时，T2＝0。‎ 出现图线a的原因是计算摆长时过短，可能是误将悬点O到小球上端的距离记为摆长，选项A错误；对于图线c，其斜率k变小了，根据k＝，可能是T变小了或L变大了，选项B中误将49次全振动记为50次，则周期T变小，选项B正确；由＝k得g＝，则k变小，重力加速度g变大，选项C错误。‎ ‎　　(4)设A点到铁锁重心的距离为l0。根据单摆的周期公式T＝2π ，得T1＝2π ，T2＝2π 。联立以上两式，解得重力加速度g＝。‎ ‎[答案]　(1)　(2)2.01　9.76　(3)B ‎(4) ‎[集训冲关]‎ ‎3．（多选）(2017·郑州质检)有两个同学利用假期分别去参观位于天津市的南开大学和上海市的复旦大学，他们各自在那里的物理实验室利用先进的DIS系统较准确的探究了单摆周期T和摆长L的关系。然后他们通过互联网交流实验数据，并由计算机绘制了T2L图像，如图甲所示，已知天津市比上海市的纬度高。另外，去复旦大学做研究的同学还利用计算机绘制了他做实验用的a、b两个摆球的振动图像，如图乙所示。则下列说法正确的是(　　)‎ A．甲图中去南开大学的同学所测得的实验结果对应的图像是B B．甲图中图线的斜率表示对应所在位置的重力加速度 C．由乙图可知，a、b两摆球振动周期之比为3∶2‎ D．由乙图可知，a、b两单摆摆长之比为4∶9‎ E．由乙图可知，t＝2 s时b球振动方向是沿＋y方向 解析：选ADE　根据单摆的周期公式T＝2π，＝，即甲图中图像的斜率为，纬度越高，重力加速度越大，斜率越小，所以去南开大学的同学所测得的实验结果对应的图像是B，选项A对；图线斜率不是重力加速度而是，选项B错；由乙图可知，a、b两摆球振动周期之比为2∶3，选项C错；由于在同一地点，重力加速度相等，根据＝可判断周期平方与摆长成正比，所以摆长之比为4∶9，选项D对；t＝2 s时，质点b在平衡位置，后一时刻质点b在平衡位置以上，所以t＝2 s时b球振动方向是沿＋y方向，选项E对。‎ ‎4．某同学在做“用单摆测重力加速度”实验中，先测得摆线长为‎101.00 cm，摆球直径为‎2.00 cm，然后用秒表记录了单摆振动50次所用的时间为101.5 s。则：‎ ‎(1)他测得的重力加速度g＝________ m/s2。‎ ‎(2)他测得的g值偏小，可能的原因是________。(填选项前面的字母)‎ A．测摆线长时摆线拉得过紧 B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了 C．开始计时，秒表过迟按下 D．实验中误将49.5次全振动数为50次 解析：(1)单摆的摆长L＝l线＋＝‎1.02 m，单摆运动的周期T＝＝ s＝2.03 s，根据单摆的周期公式T＝2π ，代入数据解得重力加速度g≈‎9.76 m/s2。‎ ‎(2)由单摆的周期公式T＝2π ，解得g＝＝，测得的g值偏小，可能是n、L测量偏小，也可能是t测量偏大造成的，故B项可能。‎ 答案：(1)9.76　(2)B ‎5.某同学利用单摆测定当地重力加速度，发现单摆静止时摆球重心在球心的正下方，他仍将从悬点到球心的距离当作摆长L，通过改变摆线的长度，测得6组L和对应的周期T，画出LT2图线，然后在图线上选取A、B两个点，坐标如图所示。他采用恰当的数据处理方法，则计算重力加速度的表达式应为g＝____________(用图中标注字母表示)。请你判断该同学得到的实验结果与摆球重心就在球心处的情况相比，将__________(填“偏大” “偏小”或“相同”)。‎ 解析：由单摆的周期公式T＝2π，得T2＝4π2，则TA 2＝4π2 ，TB2＝4π2 ，可得g＝，由此式可知测得的g与某一次实验时的摆长无关，与两次实验中的摆长差有关，所以g值与摆球重心在不在球心处无关。‎ 答案：　相同 ‎6．利用单摆测当地重力加速度的实验中。‎ ‎(1)利用游标卡尺测得金属小球直径如图甲所示，小球直径d＝________cm。‎ ‎(2)某同学测量数据如表，请在图乙中画出LT2图像。‎ L/m ‎0.400‎ ‎0.500‎ ‎0.600‎ ‎0.800‎ ‎1.200‎ T2/s2‎ ‎1.60‎ ‎2.10‎ ‎2.40‎ ‎3.20‎ ‎4.80‎ 由图像可得重力加速度g＝______m/s2(保留三位有效数字 )。‎ ‎(3)某同学在实验过程中，摆长没有加小球的半径，其他操作无误，那么他得到的实验图像可能是下列图像中的________。‎ 解析：(1)小球的直径d＝‎22 mm＋‎0.1 mm×6＝‎22.6 mm＝‎2.26 cm。‎ ‎(2)LT2图像如图所示 由T＝2π 可得：L＝T 2，k＝ 对应图像可得：k＝＝0.25‎ 可解得：g＝4π2k≈‎9.86 m/s2。‎ ‎(3)在实验中，若摆长没有加小球的半径，其他操作无误，‎ 可得：L＝T2－。故可知B正确，A、C、D均错误。‎ 答案：(1)2.26　(2)图见解析　9.86　(3)B