- 2021-05-25 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【物理】2019届一轮复习鲁科版第四章平抛运动学案
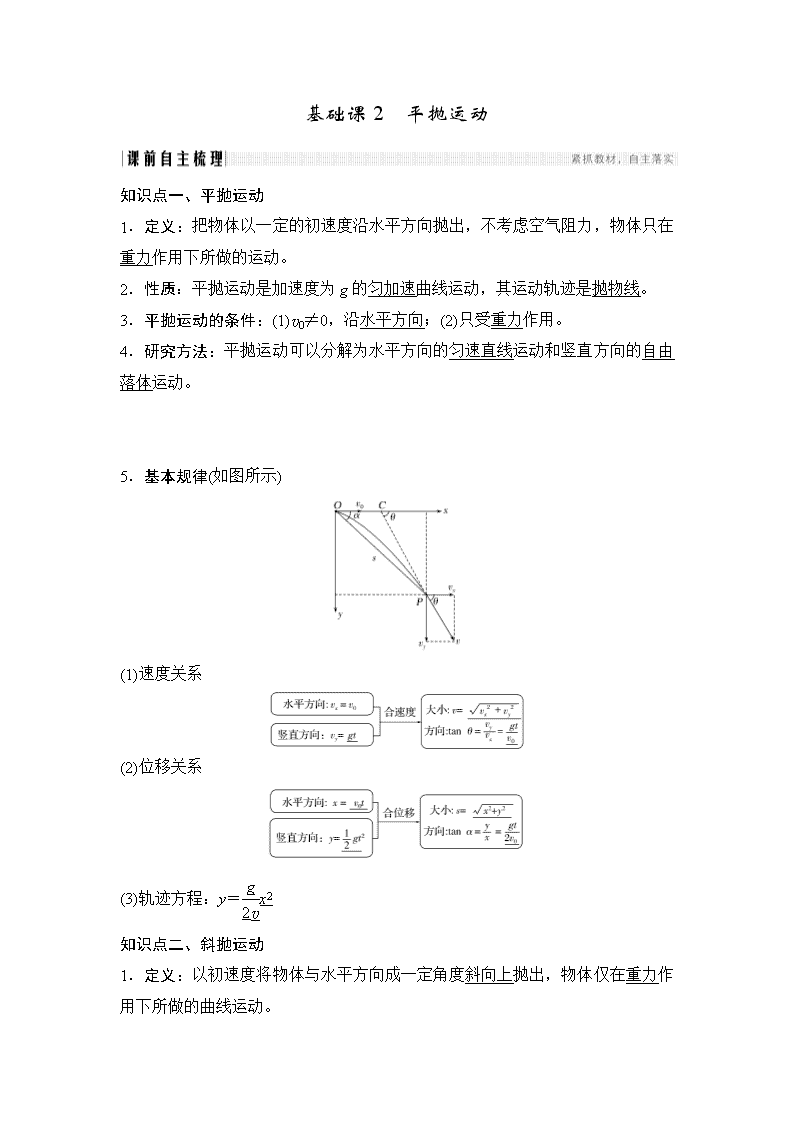
基础课2 平抛运动 知识点一、平抛运动 1.定义:把物体以一定的初速度沿水平方向抛出,不考虑空气阻力,物体只在重力作用下所做的运动。 2.性质:平抛运动是加速度为g的匀加速曲线运动,其运动轨迹是抛物线。 3.平抛运动的条件:(1)v0≠0,沿水平方向;(2)只受重力作用。 4.研究方法:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动。 5.基本规律(如图所示) (1)速度关系 (2)位移关系 (3)轨迹方程:y=x2 知识点二、斜抛运动 1.定义:以初速度将物体与水平方向成一定角度斜向上抛出,物体仅在重力作用下所做的曲线运动。 2.性质:加速度为重力加速度g的匀变速曲线运动,轨迹是抛物线。 3.研究方法:斜抛运动可以看做水平方向的匀速直线运动和竖直方向的匀变速直线运动的合运动。 [思考判断] (1)平抛运动是匀变速曲线运动。( ) (2)平抛运动的加速度方向时刻在变化。( ) (3)平抛运动的竖直分运动是自由落体运动。( ) (4)平抛运动的物体任意时刻速度方向与水平方向的夹角保持不变。( ) (5)平抛运动的物体在任意相等的两段时间内的速度的变化相同。( ) (6)对于在相同高度以相同速度平抛的物体,在月球上水平位移与在地球上水平位移相等。( ) 答案 (1)√ (2)× (3)√ (4)× (5)√ (6)× 平抛运动的规律及其应用 1.飞行时间:由t=知,时间取决于下落高度h,与初速度v0无关。 2.水平射程:x=v0t=v0,即水平射程由初速度v0和下落高度h共同决定,与其他因素无关。 3.落地速度:v==,以θ表示落地速度与x轴正方向间的夹角,有tan θ==,所以落地速度只与初速度v0和下落高度h有关。 4.速度改变量:物体在任意相等时间内的速度改变量Δv=gΔt相同,方向恒为竖直向下,如图1所示。 图1 5.两个重要推论 (1)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图2所示即xB=。 推导: ―→xB= 图2 (2)做平抛(或类平抛)运动的物体在任一时刻,设其速度方向与水平方向的夹角为θ,位移与水平方向的夹角为α,则tan θ=2tan α。如图2所示。 推导: ―→tan θ=2tan α 1.[对平抛运动的理解](多选)对于平抛运动,下列说法正确的是( ) A.落地时间和落地时的速度只与抛出点的高度有关 B.平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动 C.做平抛运动的物体,在任何相等的时间内位移的增量都是相等的 D.平抛运动是加速度大小、方向不变的曲线运动 解析 平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动,且落地时间t=,落地速度为v==,所以B项正确,A项错误;做平抛运动的物体,在任何相等的时间内,其竖直方向位移增量Δy=gt2,水平方向位移不变,故C项错误;平抛运动的物体只受重力作用,其加速度为重力加速度,故D项正确。 答案 BD 2.[平抛规律的应用](多选)某人向放在水平地面上正前方的小桶中水平抛球,结果球划着一条弧线飞到小桶的前方,如图3所示。不计空气阻力,为了能把小球抛进小桶中,则下次再水平抛球时,可能做出的调整为( ) 图3 A.减小初速度,抛出点高度不变 B.增大初速度,抛出点高度不变 C.初速度大小不变,降低抛出点高度 D.初速度大小不变,增大抛出点高度 解析 为能把小球抛进桶中,须减小水平位移,由x=v0t=v0知,选项A、C正确。 答案 AC 3.[多体的平抛运动]如图4所示,在同一平台上的O点水平抛出的三个物体分别落到a、b、c三点,不计空气阻力,则三个物体运动的初速度va、vb、vc的关系和三个物体运动的时间ta、tb、tc的关系分别是( ) 图4 A.va>vb>vc;ta>tb>tc B.va<vb<vc;ta=tb=tc C.va<vb<vc;ta>tb>tc D.va>vb>vc;ta<tb<tc 解析 三个物体做平抛运动,竖直方向为自由落体运动,由h=gt2可知,竖直位移越大,运动时间越长,所以ta>tb>tc,B、D项错误;水平方向三物体做匀速直线运动,x=v0t,由时间关系和位移关系可知,vc>vb>va,A项错误,C项正确。 答案 C 反思总结 “化曲为直”思想在平抛运动中的应用 (1)根据运动效果的等效性,利用运动分解的方法,将其转化为我们所熟悉的两个方向上的直线运动: ①水平方向的匀速直线运动; ②竖直方向的自由落体运动。 (2)运用运动合成的方法求出平抛运动的速度、位移等。 与斜面相关联的平抛运动 方法 运动情景 定量关系 总结 分解 速度 vx=v0 vy=gt tan θ== 速度方向与θ有关,分解速度,构建速度三角形 vx=v0 vy=gt tan θ== 分解 位移 x=v0t y=gt2 tan θ== 位移方向与θ有关,分解位移,构建位移三角形 【典例】 (2017·信阳一模改编)如图5所示,一名跳台滑雪运动员经过一段时间的加速滑行后从O点水平飞出,经过3 s落到斜坡上的A点。已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,不计空气阻力(sin 37°=0.6,cos 37°=0.8,g取10 m/s2)。则运动员落到斜坡上时速度方向与水平方向的夹角φ满足( ) 图5 A.tan φ=1.33 B.tan φ=1.44 C.tan φ=1.50 D.tan φ=2.00 解析 运动员落到斜坡上的瞬间,对其速度进行分解,如图所示。竖直分速度vy=gt,与水平分速度v0的比值tan φ==;竖直分位移y=gt2,与水平分位移x=v0t的比值tan θ==,可见tan θ=2tan φ=1.50,选项C正确。 答案 C 【拓展延伸】 在【典例】中,若运动员从O点飞出的初速度为20 m/s,则运动员离开O点后离斜坡的最远距离为( ) A.30 m B.15 m C.18 m D.9m 解析 将运动员的初速度v0和加速度g分别沿垂直于斜面和平行于斜面方向进行分解,如图所示,初速度v0沿垂直斜面方向上的分量为v1=v0sin θ,加速度g在垂直于斜面方向上的分量为a1=gcos θ,根据分运动各自独立的原理可知,离斜面的最大距离仅由v1和a1决定,当垂直于斜面的分速度的大小减为零时,运动员离斜面的距离最大,最大距离d===9 m。选项D正确。 答案 D 技巧点拨 平抛运动的分解方法与技巧 (1)如果知道速度的大小或方向,应首先考虑分解速度。 (2)如果知道位移的大小或方向,应首先考虑分解位移。 (3)两种分解方法: ①沿水平方向的匀速运动和竖直方向的自由落体运动; ②沿斜面方向的匀加速运动和垂直斜面方向的匀减速运动。 1.将一挡板倾斜地固定在水平面上,倾角为θ=30°,如图6所示。现有质量为m的小球由挡板上方的A点以v0的初速度水平向右抛出,小球落在挡板上的B点时,小球速度方向刚好与挡板垂直,小球与挡板碰前后的速度方向相反、速度大小之比为4∶3。下列有关小球的运动描述正确的是( ) 图6 A.小球与挡板碰后的速度为v0 B.小球与挡板碰撞过程中动量的变化量大小为mv0 C.A、B两点的竖直高度差与水平间距之比为∶1 D.A、B两点的竖直高度差与水平间距之比为∶2 解析 小球在碰撞挡板前做平抛运动。设刚要碰撞斜面时小球速度为v。由题意,速度v的方向与竖直方向的夹角为30°且水平分量仍为v0,如图。由此得v=2v0,碰撞过程中,小球速度由v变为反向的v,则碰后的速度大小为v0,A错误;碰撞过程小球的速度变化量大小为Δv=v-(-v)=v=v0,动量的变化量为mv0,故选项B错误;小球下落高度与水平射程之比为====,C错误,D正确。 答案 D 2.[分解速度和位移的综合应用](多选)如图7所示,一固定斜面倾角为θ,将小球A从斜面顶端以速率v0水平向右抛出,击中了斜面上的P点;将小球B从空中某点以相同速率v0水平向左抛出,恰好垂直斜面击中Q点。不计空气阻力,重力加速度为g,下列说法正确的是( ) 图7 A.若小球A在击中P点时速度方向与水平方向所夹锐角为φ,则tan θ=2tan φ B.若小球A在击中P点时速度方向与水平方向所夹锐角为φ,则tan φ=2tan θ C.小球A、B在空中运动的时间比为2tan2θ∶1 D.小球A、B在空中运动的时间比为tan2θ∶1 解析 由题图可知,斜面的倾角θ等于小球A落在斜面上时的位移与水平方向的夹角,由平抛运动结论可知:tan φ=2tan θ,选项A错误,B正确;设小球A在空中运动的时间为t1,小球B在空中运动的时间为t2,则由平抛运动的规律可得:tan θ=,tan θ=,则=,选项C正确,D错误。 答案 BC 平抛运动中的临界问题 常见的“三种”临界特征 (1)有些题目中有“刚好”、“恰好”、“正好”等字眼,明显表明题述的过程中存在着临界点。 (2)若题目中有“取值范围”、“多长时间”、“多大距离”等词语,表明题述的过程中存在着“起止点”,而这些起止点往往就是临界点。 (3)若题目中有“最大”“最小”“至多”“至少”等字眼,表明题述的过程中存在着极值,这个极值点往往是临界点。 【典例】 (2016·浙江理综,23)在真空环境内探测微粒在重力场中能量的简化装置如图8所示。P是一个微粒源,能持续水平向右发射质量相同、初速度不同的微粒。高度为h的探测屏AB竖直放置,离P点的水平距离为L,上端A与P点的高度差也为h。 图8 (1)若微粒打在探测屏AB的中点,求微粒在空中飞行的时间; (2)求能被屏探测到的微粒的初速度范围; (3)若打在探测屏A、B两点的微粒的动能相等,求L与h的关系。 解析 (1)打在中点的微粒h=gt2① t=② (2)打在B点的微粒v1=;2h=gt③ v1=L④ 同理,打在A点的微粒初速度v2=L·⑤ 微粒初速度范围L≤v≤L⑥ (3)由能量关系mv+mgh=mv+2mgh⑦ 代入④、⑤式L=2h⑧ 答案 (1) (2)L≤v≤L (3)L=2h 方法技巧 1.处理平抛运动中的临界问题要抓住两点 (1)找出临界状态对应的临界条件; (2)要用分解速度或者分解位移的思想分析平抛运动的临界问题。 2.平抛运动临界极值问题的分析方法 (1)确定研究对象的运动性质; (2)根据题意确定临界状态; (3)确定临界轨迹,画出轨迹示意图; (4)应用平抛运动的规律结合临界条件列方程求解。 1.[生活中的临界问题][2016·广东广州综合测试(一)]如图9,窗子上、下沿间的高度H=1.6 m,墙的厚度d=0.4 m,某人在离墙壁距离L=1.4 m、距窗子上沿h=0.2 m 处的P点,将可视为质点的小物件以v的速度水平抛出,小物件直接穿过窗口并落在水平地面上,取g=10 m/s2。则v的取值范围是( ) 图9 A.v>7 m/s B.v<2.3 m/s C.3 m/s<v<7 m/s D.2.3 m/s<v<3 m/s 解析 小物件做平抛运动,可根据平抛运动规律解题。若小物件恰好经窗子上沿,则有h=gt,L=v1t1,得v1=7 m/s,若小物块恰好经窗子下沿,则有h+H=gt,L+d=v2t2,得v2=3 m/s,所以3 m/s <v<7 m/s,故只有C项正确。 答案 C 2.[平抛运动与斜面有关的临界问题]如图10为湖边一倾角为30°的大坝横截面示意图,水面与大坝的交点为O。一人站在A点以速度v0沿水平方向扔一小石子,已知AO=40 m,不计空气阻力,g取10 m/s2。下列说法中正确的是( ) 图10 A.若v0>18 m/s,则石子可以落入水中 B.若v0<20 m/s,则石子不能落入水中 C.若石子能落入水中,则v0越大,落水时速度方向与水平面的夹角越大 D.若石子不能落入水中,则v0越大,落到斜面上时速度方向与斜面的夹角越大 解析 石子从A到O过程中,由平抛运动规律有:AO sin 30°=gt2,AO cos 30°=v0t,联立得v0=17.3 m/s,所以只要v0>17.3 m/s的石子均能落入水中,A项正确,B项错误;若石子能落入水中,由平抛运动规律有AO sin 30°=gt2,得t=2 s,则vy=gt=20 m/s,设其落水时速度方向与水平面夹角为θ,则tan θ=,vy一定,v0增大,θ减小,C项错;不落入水中时,根据“tan φ=2 tan θ”得石子落到斜面上时的速度方向与斜面夹角都相等,与v0大小无关,D项错误。 答案 A 生活中的平抛运动问题 平抛运动与日常生活紧密联系,如乒乓球、足球、排球等运动模型,飞镖、射击、飞机投弹模型等。这些模型经常受到边界条件的制约,如网球是否触网或越界、飞镖是否能击中靶心、飞机投弹是否能命中目标等。解题的关键是能准确地运用平抛运动规律分析对应的运动特征。 如图11所示,球网高出桌面H,网到桌边的距离为L,某人在乒乓球训练中,从左侧处,将球沿垂直于网的方向水平击出,球恰好通过网的上沿落到右侧边缘,设乒乓球的运动为平抛运动,下列判断正确的是( ) 图11 A.击球点的高度与网高度之比为2∶1 B.乒乓球在网左右两侧运动时间之比为2∶1 C.乒乓球过网时与落到右侧桌边缘时速率之比为1∶2 D.乒乓球在左、右两侧运动速度变化量之比为1∶2 解析 因为水平方向做匀速运动,网右侧的水平位移是左边水平位移的两倍,所以网右侧运动时间是左侧的两倍,竖直方向做自由落体运动,根据h=gt2可知,击球点的高度与网高之比为9∶8,故A、B错误;球恰好通过网的上沿的时间为落到右侧桌边缘的时间的,竖直方向做自由落体运动,根据v=gt可知,球恰好通过网的上沿的竖直分速度与落到右侧桌边缘的竖直分速度之比为1∶3,根据v=可知,乒乓球过网时与落到桌边缘时速率之比不是1∶2,故C错误;网右侧运动时间是左侧的两倍,Δv=gt,所以乒乓球在左、右两侧运动速度变化量之比为1∶2,故D正确。 答案 D (2015·浙江理综)如图12所示为足球球门,球门宽为L。一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点)。球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( ) 图12 A.足球位移的大小x= B.足球初速度的大小v0= C.足球末速度的大小v= D.足球初速度的方向与球门线夹角的正切值tan θ= 解析 足球位移大小为x==,A错误;根据平抛运动规律有:h=gt2,=v0t,解得v0=,B正确;足球的末速度v===, C错误;足球初速度方向与球门线夹角正切值tan θ==,D错误。 答案 B 反思总结 处理此类问题的方法 (1)阅读试题,提炼关键信息;(2)通过迁移、联想、类比,建立物理模型;(3)找出每个物理过程所满足的规律,应用所学知识列方程,进行推理计算,得出结论。 体育运动中许多运动都可简化为平抛运动的模型,在分析此类问题时一定要注意从实际出发寻找一些临界点,画出物体运动的草图,找出临界条件,如图所示的网球刚好过网和刚好压线的情况。 1.(2016·海南单科,1)在地面上方某一点将一小球以一定的初速度沿水平方向抛出,不计空气阻力,则小球在随后的运动中( ) A.速度和加速度的方向都在不断变化 B.速度与加速度方向之间的夹角一直减小 C.在相等的时间间隔内,速率的改变量相等 D.在相等的时间间隔内,动能的改变量相等 解析 由于物体做平抛运动,故物体只受重力作用,加速度不变,速度的大小和方向时刻在变化,故选项A错误;设某时刻速度与竖直方向夹角为θ,则tan θ==,随着时间t的变大,故tan θ变小,则θ变小,故选项B 正确;根据加速度定义式a==g,则Δv=gΔt,即在相等的时间间隔内,速度的改变量相等,故选项C错误;根据动能定理,在相等的时间间隔内,动能的改变量等于重力的功,即WG=mgh,而平抛运动在相等时间内竖直方向上的位移不相等,故选项D错误。 答案 B 2.(全国卷)(多选)如图13所示,x轴在水平地面内,y轴沿竖直方向。图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的。不计空气阻力,则( ) 图13 A.a的飞行时间比b的长 B.b和c的飞行时间相同 C.a的水平速度比b的小 D.b的初速度比c的大 解析 根据平抛运动的规律h=gt2,得t= ,因此平抛运动的时间只由高度决定,因为hb=hc>ha,所以b与c的飞行时间相同,大于a的飞行时间,因此选项A错误,B正确;又因为xa>xb,而ta查看更多