平抛运动研究·典型例题精析

平抛运动研究·典型例题精析

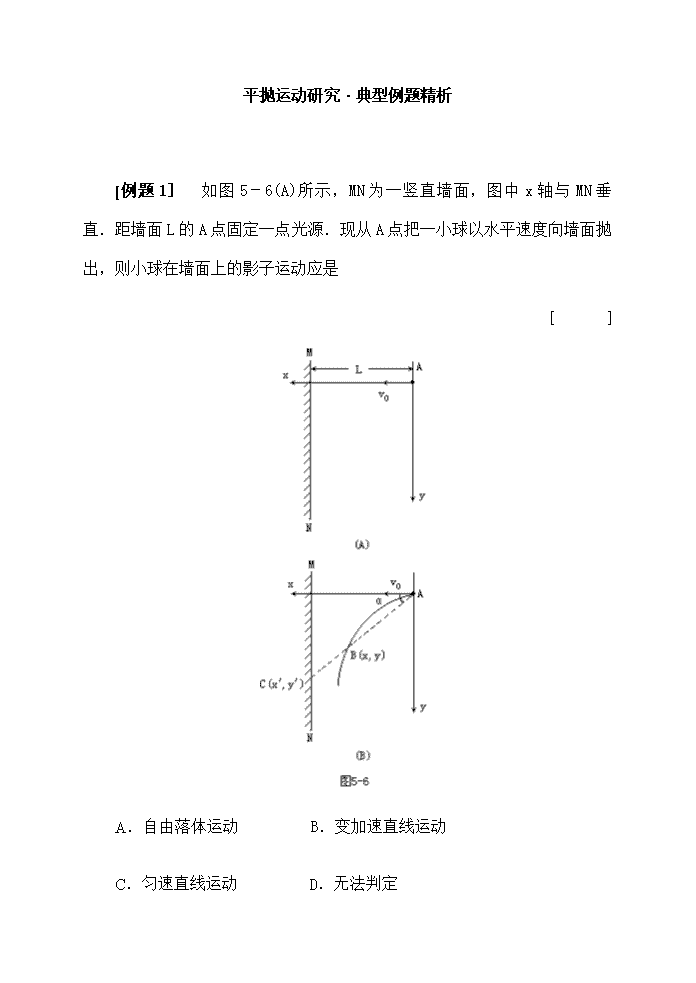
平抛运动研究·典型例题精析 ‎ ‎ ‎[例题1]　 如图5－6(A)所示，MN为一竖直墙面，图中x轴与MN垂直．距墙面L的A点固定一点光源．现从A点把一小球以水平速度向墙面抛出，则小球在墙面上的影子运动应是 ‎[　　　 ]‎ A．自由落体运动　　　　 B．变加速直线运动 C．匀速直线运动　　　　 D．无法判定 ‎[思路点拨]　 小球抛出后为平抛运动，在图中x方向上为匀速直线运动，在y方向上为自由落体运动．故不少同学选择(A)项，而实际上该答案是错误的．问题在于我们研究的并不是小球在竖直方向上的运动，而是在点光源照射下小球在墙上影子的运动．‎ ‎[解题过程]　 设小球从A点抛出后经过时间t，其位置B坐标为(x，y)，连接AB并延长交墙面于C(x′，y′)．显然C点就是此时刻小球影子的位置(如图5－6(B)所示)．‎ 令AB与x轴夹角为α，则 依几何关系，影子位置y′＝L·tanα．故 令　 gL/2v0＝k，则y′＝k·t．‎ 即影子纵坐标y′与时间t是正比例关系，所以该运动为匀速直线运动，应选(C)项．‎ ‎[小结]　 (1)要认真审清题意：本题所研究的是“点光源照射下小球影子的运动”，否则会差之毫厘，谬之千里．‎ ‎(2)对选择题的分析判断，切莫主观猜测，要做到弃之有理，选之有据．对于需做出定量研究的问题，最好的方法就是将物理图景利用数学语言表达出来，例如在本题中就是写出位移随时间的函数关系．‎ ‎[例题2] 　如图5－7所示，M和N是两块相互平行的光滑竖直弹性板．两板之间的距离为L，高度为H．现从M板的顶端O以垂直板面的水平速度v0抛出一个小球．小球在飞行中与M板和N板，分别在A点和B点相碰，并最终在两板间的中点C处落地．求：‎ ‎(1)小球抛出的速度v0与L和H之间满足的关系；‎ ‎(2)OA、AB、BC在竖直方向上距离之比．‎ ‎[思路点拨]　 ‎ 根据平抛运动规律，建立小球在MN之间的运动图景是本题关键之一．小球被水平抛出后，如果没有板面N的作用，其运动轨迹应如图5－8中虚线所示．由于板面光滑弹性良好，故在A点与N板碰后，应满足反射定律，反弹后运动轨迹与虚线，满足以N板为轴的左右对称．第二次在B点与M板相碰情况亦然．本题的另一难点是问题 竖直方向运动为自由落体，所以不少同学会认为这三段在竖直方向上距离之比应为：1∶3∶2.5．你是否也有同样的结果呢？‎ ‎[解题过程]　 (1)分析可知运动的全过程中，小球始终保持其水平速度大小v0不变．设运动全过程飞行时间为t，水平全程长度为S，则 又　　　　　　　　　　　　　　　　 S＝2.5L，‎ ‎(2)取小球由B到C为一个时间间隔Δt．小球从O抛出到C点落地共经过5个Δt．在此5个Δt中下落高度之比为：1∶3∶5∶7∶9．‎ 由于tOA包括第1个Δt和第2个Δt；tAB包括第3个Δt和第4个Δt，故三段竖直距离之比为 hOA∶hAB∶hBC＝(1＋3)∶(5＋7)∶9＝4∶12∶9．‎ ‎[小结]　 (1)注意将平抛运动的一般规律与题目中特定物理条件相结合，才能正确描述题目的物理图景。‎ ‎(2)要注意反思．例如对上述所说的三段竖直距离之比为什么不是1∶3∶2.5这个关系，显然是从初速度为零的匀变速直线运动，在连续相等时间间隔内位移之比为1∶3∶5…而来，同时又考虑到BC段时间仅为每段时间一半，所以下落竖直距离也是一半．这种错误，稍加反思即可避免．试想匀加速运动前半程与后半程时间内运动距离怎么能相等呢！对问题的反思很重要，它常可使自己对问题的认识得以深化．‎ ‎[例题3] 　标准排球场总长度18 m，女排比赛网高2.24 m，在一场校际比赛中，女排队员李芳在后排起跳强攻的位置刚好在距网3m的正上方，然而她击球速度(水平方向)无论多大，不是下网就是出界，试分析其原因(设球被击出后做平抛运动)．‎ ‎[思路点拨]　 当击球位置到球网水平距离恒定时，依平抛运动规律可知，排球被水平击出的初速越大，越不容易触网；但若速度过大，又会击球出界．显然为使球不触网，球速必应大于某值A；而为使之不出界，球速又应小于某值B．为使之既不触网又不出界，则必须满足：B≥v0≥A．但若按平抛规律求得结果A比B还大，物理现象怎样呢？那就是说：初速v0如果小于A必触网；初速v0如果大于A，则必大于B，故必出界．这就是题目中所出现的情况，而究其原因就在于击球点的高度不够．‎ ‎[解题过程]　 设李芳击球点高度为h，为保证其击球不下网，初速应满足 为使击球不出界，应满足 ‎[小结]　 (1)本题应从哪里切入求解是初学者的难点，在此科学而严密的逻辑推理得到充分体现．题目中问题有两个层面：下网和出界．由平抛运动规律可推知：为保证排球既不会下网，又不会出界，应满足：A≤v0≤B．而题目中明确指出：“击球速度无论多大，不是下网就是出界．”这就是说按平抛规律求解出的A和B之间，不存在A＜B，而是B＜A．这就是本题的切入点．‎ ‎(2)本题是排球场上的实际问题，能用自己的所学，去分析、研究乃至解决实际问题，是我们在学习中要培养的重要能力之一，同学们在学习中应给予足够关注．‎ ‎ ‎