气体实验定律1

气体实验定律1

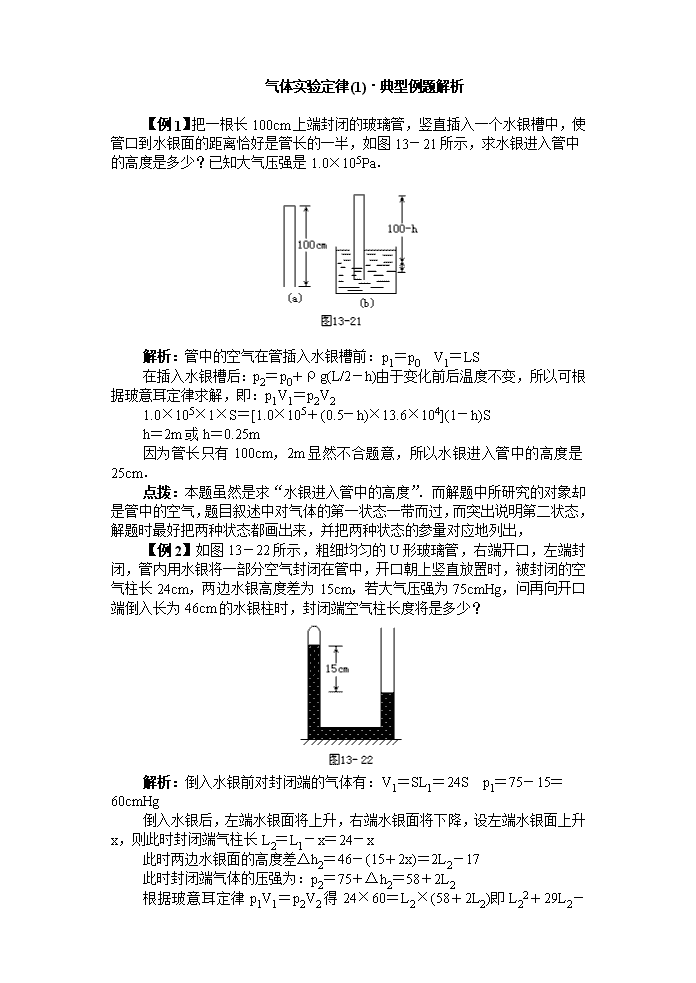
气体实验定律(1)·典型例题解析 【例 1】把一根长 100cm 上端封闭的玻璃管，竖直插入一个水银槽中，使 管口到水银面的距离恰好是管长的一半，如图 13－21 所示，求水银进入管中 的高度是多少？已知大气压强是 1.0×105Pa． 解析：管中的空气在管插入水银槽前：p1＝p0 V1＝LS 在插入水银槽后：p2＝p0＋ρg(L/2－h)由于变化前后温度不变，所以可根 据玻意耳定律求解，即：p1V1＝p2V2 1.0×105×1×S＝[1.0×105＋(0.5－h)×13.6×104](1－h)S h＝2m 或 h＝0.25m 因为管长只有 100cm，2m 显然不合题意，所以水银进入管中的高度是 25cm． 点拨：本题虽然是求“水银进入管中的高度”．而解题中所研究的对象却 是管中的空气，题目叙述中对气体的第一状态一带而过，而突出说明第二状态， 解题时最好把两种状态都画出来，并把两种状态的参量对应地列出， 【例 2】如图 13－22 所示，粗细均匀的 U 形玻璃管，右端开口，左端封 闭，管内用水银将一部分空气封闭在管中，开口朝上竖直放置时，被封闭的空 气柱长 24cm，两边水银高度差为 15cm，若大气压强为 75cmHg，问再向开口 端倒入长为 46cm 的水银柱时，封闭端空气柱长度将是多少？ 解析：倒入水银前对封闭端的气体有：V1＝SL1＝24S p1＝75－15＝ 60cmHg 倒入水银后，左端水银面将上升，右端水银面将下降，设左端水银面上升 x，则此时封闭端气柱长 L2＝L1－x＝24－x 此时两边水银面的高度差Δh2＝46－(15＋2x)＝2L2－17 此时封闭端气体的压强为：p2＝75＋Δh2＝58＋2L2 根据玻意耳定律 p1V1＝p2V2 得 24×60＝L2×(58＋2L2)即 L2 2＋29L2－720 ＝0 解得：L2＝－45cm(舍去)，L2＝16cm． 点拨：确定两边水银面的高度差以及由高度差求被封气体的压强是解答本 题的关键． 【例 3】将两端开口的长 60cm 的玻璃管竖直插入水银中 30cm，将上端开 口封闭，而后竖直向上将管从水银中提出，再将管口竖直向上，若大气压强为 76cmHg，求气柱长？ 点拨：当管从水银中取出时，有一部分水银将流出，求出此时水银柱的长 度，才能求出玻璃管开口向上时气体的压强，最后才能解决气柱长度问题． 参考答案：23.9cm 【例 4】如图 13－23 所示，一个上下都与大气相通的直圆筒，内部横截 面的面积 S0＝0.01m2，中间用两个活塞 A 和 B 封住一定质量的理想气体，A、 B 都可沿圆筒无摩擦地上、下滑动，但不漏气，A 的质量可不计，B 的质量为 M，并与一劲度系数 k＝5×103N/m 的较长的弹簧相连，已知大气压强 p0＝1× 105Pa．平衡时，两活塞间的距离 L0＝0.6m，现用力压 A，使之缓慢向下，移 动一定距离后，保持平衡，此时用于压 A 的力 F＝5×102N，求活塞 A 向下移 动的距离．(假设气体温度保持不变) 点拨：A 下降的距离等于气柱变短的长度和 B 下移的距离之和，以整体为 研究对象分析弹簧缩短的距离，用玻意耳定律分析密封气柱的长度的变化，可 以通过画图使之形象化． 参考答案：0.3m 跟踪反馈 1．一个空气泡从湖的深处冒上来，如果湖水温度处处相等，则气泡上升 过程中受到的浮力将： [ ] A．逐渐增大 B．逐渐减小 C．保持不变 D．无法确定 2．一根一端封闭的均匀玻璃管水平放置，其间有一段 21.8cm 的水银柱， 将长为 30.7cm 的空气柱封闭在管中，若将玻璃管开口竖直向上时，空气柱长 度为多少？若将玻璃管开口竖直向下时，空气柱长度为多少？(设外界大气压强 为 74.7cm Hg) 3．在标准状况下，一个气泡从水底升到水面，它的体积增大一倍，求水 深 h．(g 取 10m/s2) 4．两端封闭的均匀细玻璃管水平放置，管的正中央有一段长 15cm 的水 银柱，其两侧的空气柱中的压强均为 72cmHg，现将玻璃管旋至竖直位置，若 欲使玻璃管中上、下两段空气柱的长度保持为 1∶2，则玻璃管沿竖直方向做什 么样的运动？设整个过程中，温度保持恒定． 参考答案 1．A 2．24cm、48cm 3．10m 4．a＝4.6m/s2，竖直向下加速