【物理】2018届一轮复习人教版光的折射、全反射学案
第76课时 光的折射、全反射(重点突破课)
[必备知识]
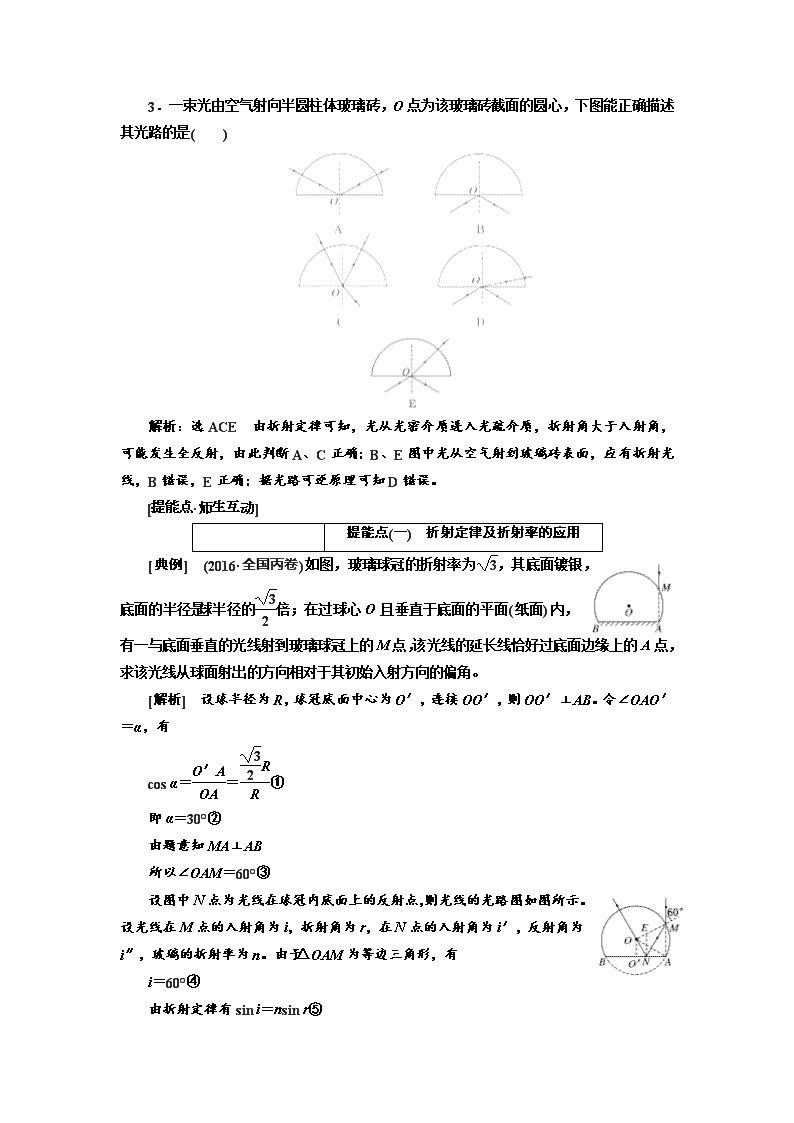
一、光的折射定律 折射率
1.折射现象
光从一种介质斜射进入另一种介质时传播方向发生改变的现象,如图所示。
2.折射定律
(1)内容:折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比。
(2)表达式:=n12,式中n12是比例常数。
3.折射率
(1)物理意义:折射率反映介质的光学特性,折射率大,说明光从真空射入到该介质时偏折大,反之偏折小。
(2)定义式:n=,不能说n与sin θ1成正比,与sin θ2成反比。折射率由介质本身的光学性质和光的频率决定。
(3)计算公式:n=。
二、全反射 光导纤维 光的色散
1.全反射
(1)定义:光从光密介质射入光疏介质,当入射角增大到某一角度时,折射光线将消失,只剩下反射光线的现象。
(2)条件:①光从光密介质射向光疏介质。
②入射角大于等于临界角。
(3)临界角:折射角等于90°时的入射角。若光从光密介质(折射率为n)射向真空或空气时,发生全反射的临界角为C,则sin C=。介质的折射率越大,发生全反射的临界角越小。
2.光导纤维
光导纤维的原理是利用光的全反射。
3.光的色散
(1)色散现象:白光通过三棱镜会形成红、橙、黄、绿、蓝、靛、紫七种色光组成的彩色光谱。
(2)成因:由于n红
,将发生全反射,C图错误,D图正确;sin 30°=<,不会发生全反射,E图正确。
2.如图所示,从点光源S发出的一细束白光以一定的角度入射到三棱镜的表面,经过三棱镜的折射后发生色散现象,在光屏的ab间形成一条彩色光带。下面的说法中正确的是( )
A.a侧是红光,b侧是紫光
B.在真空中a侧光的波长小于b侧光的波长
C.三棱镜对a侧光的折射率大于对b侧光的折射率
D.在三棱镜中a侧光的速率比b侧光小
E.在三棱镜中a、b两侧光的速率相同
解析:选BCD 由题图可以看出,a侧光偏折得较厉害,三棱镜对a侧光的折射率较大,所以a侧光是紫光,波长较短,b侧光是红光,波长较长,因此A错,B、C正确;又v=,所以三棱镜中a侧光的传播速率小于b侧光的传播速率,D正确,E错误。
3.如图所示是一玻璃球体,其半径为R,O为球心,AB为水平直径。M点是玻璃球的最高点,来自B点的光线BD从D点射出,出射光线平行于AB,已知∠ABD=30°,光在真空中的传播速度为c,则( )
A.此玻璃的折射率为
B.光线从B到D需用时
C.该玻璃球的临界角应小于45°
D.若增大∠ABD,光线不可能在DM段发生全反射现象
E.若减小∠ABD,从AD段射出的光线均平行于AB
解析:选ABC 由题图可知光线在D点的入射角为i=30°,折射角为r=60°,由折射率的定义得n=知n=,A正确;光线在玻璃中的传播速度为v==c,由题图知BD=R,所以光线从B到D需用时t==,B正确;若增大∠ABD,则光线射向DM段时入射角增大,射向M点时为45°,而临界角满足sin C==<=sin 45°,即光线可以在DM段发生全反射现象,C正确,D错误;要使出射光线平行于AB,则入射角必为30°,E错误。
4.(2016·石家庄一中检测)直线P1P2过均匀玻璃球球心O,细光束a、b平行且关于P1P2对称,由空气射入玻璃球的光路如图。a、b光相比( )
A.玻璃对a光的折射率较小
B.玻璃对a光的临界角较大
C.b光在玻璃中的传播速度较小
D.b光在玻璃中的传播时间较短
E.两种光在玻璃中的传播时间相等
解析:选ABC 由题图可判断出玻璃对光束b的折射率大于光束a,A正确;根据公式sin C=,可知玻璃对a光的临界角大于b光的临界角,B正确;根据公式n=,可知b光在玻璃中的传播速度比a光小,C正确;根据以上分析可知,b光在玻璃中走过的距离比a光大,同时传播速度比a光小,于是传播时间比a光长,D、E错误。
二、计算题
5.如图所示为一半球壳形玻璃砖,其折射率为n=,球壳内圆的半径为R,外圆的半径为R。图中的OO′为半球壳形玻璃砖的中轴线,一束平行光以平行于OO′的方向从球壳的左侧射入,如图所示。若使光第一次到达内圆表面时能射出,求入射角i的范围。
解析:作出光路图如图所示。设光线AB入射到球壳的外表面,沿BM方向射向内圆,刚好发生全反射,
则sin C==,故C=45°
在△OBM中,OB=R,OM=R
所以=
sin r==,则r=30°
由折射定律得n=
则sin i=nsin r=,故i=45°
当射向半球壳外表面的入射光线的入射角i<45°时,这些光线都会从内圆表面射出。
答案:i<45°
6.(2017·贵州黔南州三校联考)细束平行光以一定的入射角从空气射到直角棱镜的侧面AB,光线进入棱镜后直接射向另一侧面AC。逐渐调整光线在AB面的入射角,使AC面恰好无光线射出,测得此时光线在AB面的入射角为α。
(1)画出光线在AB面的入射角为α时,在AB面、AC面两次折射的光路图;
(2)计算该棱镜的折射率。
解析:(1)画出光线在AB面的入射角为α时恰在AC面全反射,折射光线沿AC面传播,光路如图。
(2)由于光在AC面恰好全反射。故有:sin γ= ,
由几何关系有:β+γ=,
对光在AB面的折射有:=n。
解得棱镜折射率为:n=。
答案:(1)见解析图 (2)
7.投影仪的镜头是一个半球形的玻璃体,光源产生的单色平行光投射到平面上,经半球形镜头折射后在光屏PQ上形成一个圆形光斑。已知半球形镜头半径为R,光屏PQ到球心O的距离为d(d>3R),玻璃对该单色光的折射率为n,不考虑光的干涉和衍射,真空中光速为c。求:
(1)光在半球形镜头中的速度。
(2)光屏PQ上被照亮光斑的面积。
解析:(1)由n=解得:v=。
(2)如图所示,设光线入射到D点时恰好发生全反射,
sin C= ,
===
又因为=tan C
=d-
解得r=d-nR
光屏PQ上被照亮光斑的面积S=πr2=π(d-nR)2。
答案:(1) (2)π(d-nR)2
8.(2016·全国乙卷)如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0 m。从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为。
(1)求池内的水深;
(2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m。当他看到正前下方的点光源A时,他的眼睛所接受的光线与竖直方向的夹角恰好为45°。求救生员的眼睛到池边的水平距离(结果保留1位有效数字)。
解析:(1)如图,设到达池边的光线的入射角为i,依题意,水的折射率n=,光线的折射角θ=90°。由折射定律有
nsin i=sin θ①
由几何关系有
sin i=②
式中,l=3.0 m,h是池内水的深度。
联立①②式并代入题给数据得
h= m≈2.6 m。③
(2)设此时救生员的眼睛到池边的距离为x。依题意,救生员的视线与竖直方向的夹角为θ′=45°。由折射定律有nsin i′=sin θ′④
式中,i′是光线在水面的入射角。设池底点光源A到水面入射点的水平距离为a。由几何关系有
sin i′=⑤
x+l=a+h′⑥
式中h′=2 m。联立③④⑤⑥式得
x=m≈0.7 m。⑦
答案:(1)2.6 m (2)0.7 m