- 2021-05-24 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【物理】2019届一轮复习人教版闭合电路欧姆定律应用模型学案
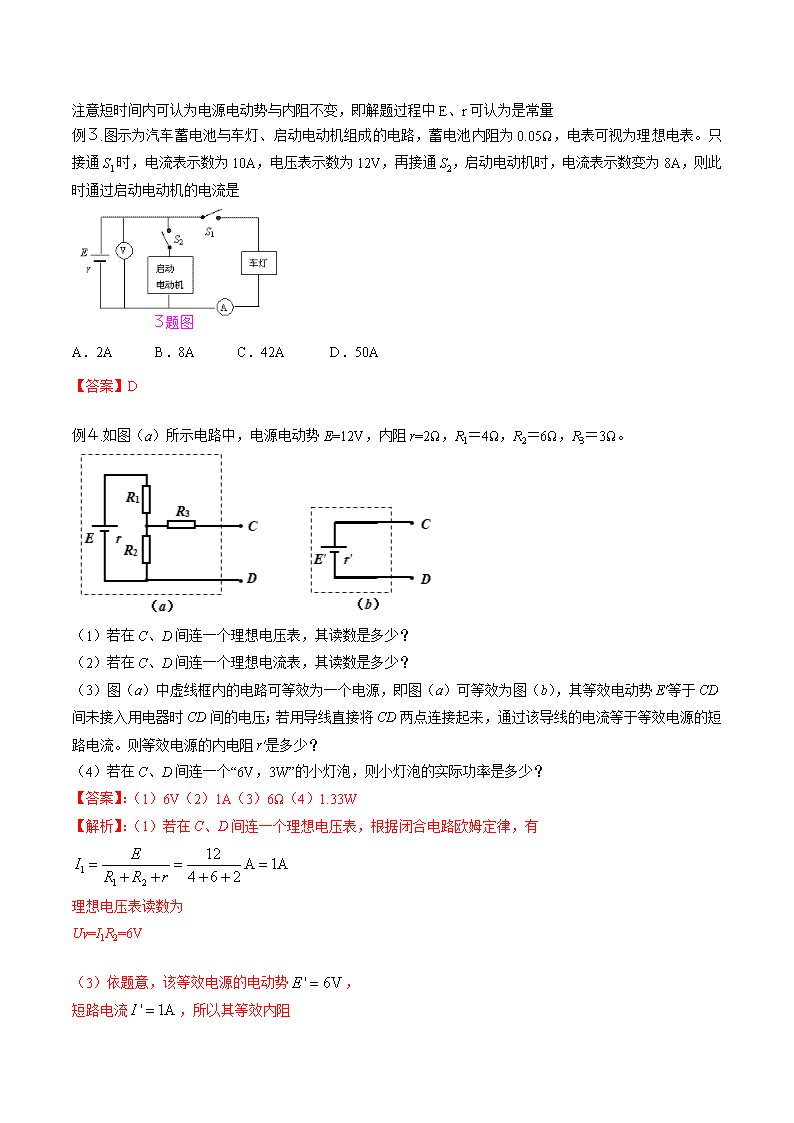
模型界定 在闭合电路中,涉及电路结构的分析与简化;涉及元件有电键、电表及纯电阻、非纯电阻元件;涉及问题涵盖电流、电压、电动势、功率、效率及图像;应用规律有部分电路与全电路欧姆定律、焦耳定律、能量守恒、功率与效率公式、串并联电路基本关系等 模型破解 1.解决电路题目的首要问题是电路结构的分析与简化,简化电路时可用节点法、电流流向法、等电势法等。每种方法中都需注意一些特殊情况的处理: (1)电表处理:理想电流表用导线替代,理想电压表处断开。非理想电表等效为一个电阻。 (2)电容器处理:在电路稳定即电容器非充放状态下电容器所在电路是断路的 (3)无电流通过的电阻处理:与理想电压表、电容器串联的定值电阻中无电流通过,其两端电压为0、电势相等,此时可用一无电阻的导线替代 (4)滑动变阻器的处理:由滑片所在处将滑动变阻器的总电阻分成两部分,限流式接法中一部分被短路、一部分接入电路;分压式接法中一部分与测量电路并联再与另一部分相串联 例1.一个T型电路如图所示,电路中的电=10,=120,。另有一侧是电源,电动势为100V,内阻忽略不计。则 A.当端短路时,之间的等效电阻是 B.当端短路时,之间的等效电阻是40 C.当两端接通测试电源时,两端的电压为80V D.当两端接通测试电源时,两端的电压为80V 【答案】AC 【解析】当cd端短路时,电路结构为R2与R3并联后再与R1串联,,同理可知 ,A正确B错误。当ab两端接电源时,cd间接入电压表测电压时,R2可等效为一条导线,cd两端的电压等于电阻R2两端电压,同理有C正确D错误。 例2. 如图所示电路中,A1和A2为理想电流表,示数分别为I1和I2,。当a、b两点间加以恒定的电压U后,下列结论正确的是( ) A.I1:I2=3:4 B.I1:I2=5:9 C.将A1、A2换理想电压表,其示数之比为3:5 D.将A1、A2换理想电压表,其示数之比为1:1 【答案】BC 2.应用欧姆定律列式的再一个查看外电路中有无非纯电阻器件。欧姆定律U=IR只适用于纯电阻器件;对于全电路欧姆定律的两个表达式要注意到 (1)表达式E=I(R+r)适用于外电路不含有非纯电阻的元件 + + (2)表达式E=U+Ir对外电路有无非纯电阻元件都适用 另外,若是一个电池处于被充电的状态时,电池两端电压与其电动势的关系是U=E+Ir 最后根据已知量与待求量利用全电路欧姆定律和部分电路的欧姆定律、串并联电路中电流、电压间关系列方程求解 注意短时间内可认为电源电动势与内阻不变,即解题过程中E、r可认为是常量 例3.图示为汽车蓄电池与车灯、启动电动机组成的电路,蓄电池内阻为0.05Ω,电表可视为理想电表。只接通S1时,电流表示数为10A,电压表示数为12V,再接通S2,启动电动机时,电流表示数变为8A,则此时通过启动电动机的电流是 3题图 A.2A B.8A C.42A D.50A 【答案】D 例4.如图(a)所示电路中,电源电动势E=12V,内阻r=2Ω,R1=4Ω,R2=6Ω,R3=3Ω。 (1)若在C、D间连一个理想电压表,其读数是多少? (2)若在C、D间连一个理想电流表,其读数是多少? (3)图(a)中虚线框内的电路可等效为一个电源,即图(a)可等效为图(b),其等效电动势E′等于CD间未接入用电器时CD间的电压;若用导线直接将CD两点连接起来,通过该导线的电流等于等效电源的短路电流。则等效电源的内电阻r′是多少? (4)若在C、D间连一个“6V,3W”的小灯泡,则小灯泡的实际功率是多少? 【答案】:(1)6V(2)1A(3)6Ω(4)1.33W 【解析】:(1)若在C、D间连一个理想电压表,根据闭合电路欧姆定律,有 理想电压表读数为 UV=I1R2=6V (3)依题意,该等效电源的电动势, 短路电流,所以其等效内阻 (4)小灯泡的电阻 将小灯泡连在C、D之间,相当于接在等效电源E′两端,则流过小灯泡的电流大小为 小灯泡的实际功率为 3.电流是电路问题的灵魂,除了可从欧姆定律求解电流外,还可从电流定义式I=q/t及微观表达式 I=nqSv=λqv、焦耳定律Q=I2Rt、电功率P=IU、电源功率P=IE及输出功率P=IU、内电路功率P=I2r、串并联电路中电流关系等求解 一般说来,涉及通过导体横截面电荷量、自由电荷数目、定向运动速度等问题时利用电流定义式或微观表达式;应用电路结构求电流时,若电路不是简单的串并联结构时,可利用通过节点的电流关系:流入节点的总电流与流出节点的总电流相等 例5.如图是一个电路的一部分,其中R1=5Ω,R2=1Ω,R3=3Ω,I1=0.2A,I2=0.1A,那么电流表测得的电流为 例5图 A.0.2 A,方向向右 B.0.15A,方向向左 C.0.2 A,方向向左 D.0.3A,方向间右 【答案】C 4.在电源的输出功率问题中,注意电源的输出功率随电流或外电路的电阻不是单调变化,要利用PR-I、PR-R关系图线的特点分析求解,常用推论有: (1)当I=E/2r=I短/2时输出功率最大,电路中电流不能达到E/2r=I短/2时则越接近输出功率越大 (2)外电路是纯电阻前提下,当R=r时电源的输出功率最大。外电路阻值不能达到r时则R越接近r输出功率越大 (3)当输出功率小于电源的最大输出功率时,同一输出功率值可对应于电路中的两个电流值、两个外电路的电阻值,两个值之间的关系为I1+I2=I短,R1R2=r2 另外,求某一可变电阻消耗的最大功率时较简便的方法是“等效电源”法 例6.当外电路的电阻分别为8 Ω和2 Ω时,单位时间内在外电路上产生的热量正好相等,则该电源的内电阻是( ) A.1 Ω B.2 Ω C.4 Ω D.6 Ω 【答案】C 【解析】:由()2R1=()2R2,代入数据解得r=4 Ω,C正确.也可直接由推论R1R2=r2得结果。 例7 如图所示,R1为定值电阻,R2为可变电阻,E为电源电动势,r为电源的内电阻,以下说法中错误的是 A.当R2=Rl + r时,R2上获得最大功率 B.当Rl=R2 + r时,Rl上获得最大功率 C.当R2=O时Rl上获得功率可能最大 D.当R2=O时,电源的输出功率可能最大 【答案】:B 5.在串并电路中,给定了各器件的额定功率时,电路中能消耗的最大功率并一定等于各器件额定功率之和,电流电压也存在同样的问题。此类问题解题的基本思路是: (1)串联电路中比较额定电流,取其小者计算出总电压、总功率即为最大值 (2)并联电路中比较额定电压,取其小者计算总电流、总功率即为最大值 例8.R1、R2和R3分别标有“”、“”和“”将它们连接后接入电路中,如右图所示,则此电路中允许消耗的最大功率为 A.0.4W B.2.2W C.2.5 W D.3.4W 【答案】A 【解析】:两电阻串联,通过的电流相等,允许通过的最大电流取其额定电流的最小值,即上支路中最大电流Im=0.5A,则该支路两端电压最大值为Um1=Im(R1+R2)=2.5V。并联电路中电压相等,所能加的最大电压取两端电压的最小值,而R3的额定电压为1V,故整个电压所能加的最大电压为Um2=U3=1V,电路中允许消耗的最大功率Pm=I3U3+U32/(R1+R2)=0.4W,A正确。 6.在涉及图像的常见问题中,涉及电源总功率P=IE、电源的输出功率(外电路消耗的功率)PR=IU=I(E-Ir)、电源的热功率(电源内电路消耗的电功率)Pr=I2r在同一坐标系中图像的分析与计算,注意与函数表达式对应起来分析; 电源的外伏安特性曲线与导体伏安特性曲线在同一坐标中图像的分析与计算,注意两图像的交点坐标表示该导体与该电源组成闭合回路时的工作点;注意图像上某点斜率的意义及区分切线斜率与连线斜率;注意面积的物理意义及如何从图像上分析电源的效率等 例9.某同 将一直流电源的总功率PE、输出功率PR和电源内部的发热功率P,随电流I变化的图线画在了同一坐标系上,如图中的a、b、c所示,根据图线可知 A. 反映变化的图线是c B. 电源电动势为8V C. 电源内阻为1 D. 当电流为0.5A时,外电路的电阻为6 【答案】AD 例10.已知两个电源的电动势为E1和E2、内阻r1和r2满足关系E2>E1,r2>r1,有一定值电阻R1分别接在两个电源上,获得相等的功率,则去掉R1而将另一电阻R2且满R2>R1分别接在该两个电源上,关于电阻R2获得的功率P2有 A.P1< P2 B.P1>P2 C.P1= P2 D.条件不足无法确定 【答案】A 【解析】:此时用解析式分析时涉及的变量较多,不易分析,可考虑用图象法。由于定值电阻在两电源上获取的功率相等,则两电源的U-I图线必有交点,且导体的U-I图线与它们交于同一点上,作出图像如图所示。 将R2接在两电源上时,由图可以看出,图线与两电源U-I图线的交点坐标线所围矩形面积相比,接在电动势较大的E1上时输出功率即R2消耗的功率较大,A正确。 题型演练 1.玻尔认为,围绕氢原子核做圆周运动的核外电子,轨道半径只能取某些特殊的数值,这种现象叫做轨道的量子化。若离核最近的第一条可能的轨道半径为r1,则第n条可能的轨道半径为(n=1,2,3,……),其中n叫量子数。设氢原子的核外电子绕核近似做匀速圆周运动形成的等效电流,在n=3状态时其强度为I,则在n=2状态时等效电流强度为 A. B. C. D. 【答案】C 2.一质子源发出的初速度为0的质子,经一加速电场加速,形成了1mA的细柱形质子流。已知质子的电荷e=1.60×10-19C (1)每秒钟靶上接收到的质子数为多少? (2)假定靶与质子源之间的电场是均匀分布的,在质子束中距质子源L和4L处各取一段极短的相等长度的质子流,其中质子数分别为n1和n2,求n1:n2 【答案】:(1)6.25×1015(2)2:1 【解析】:(1)由电流的定义式 可得每秒靶上接收的质子数为 3.如图所示电路中,R=4Ω,R2=6Ω,电源内阻不可忽略,当电键S2闭合时,电流表A的示数为3 A,则当S2断开时,电流表示数可能为 ( ) A.3.2 A B.2.1 A C.1.2 A D.0.8 A 【答案】B 【解析】:断开后,总电阻变大,电流变小,A错误.原来路端电压是12 V,后来路端电压大于12 V,电流则大于1.2 A.CD皆错误,B正确. 4.在图甲所示电路中,R1、R2均为定值电阻,且R1=100 Ω,R2的阻值未知,R3是一滑动变阻器,当其滑片从最左端滑至最右端的过程中,测得电源的路端电压U随电流I的变化图线如图乙所示,其中图线上的A、B两点是滑片在变阻器上的两个不同端点时分别得到的.求: 甲 乙 (1)电源的电动势和内电阻; (2)定值电阻R2的阻值; (3)滑动变阻器R3的最大值. 【答案】:(1)20V 20Ω(2)5Ω(3)300Ω 【解析】:(1)由闭合电路欧姆定律得: E=U+Ir 将图象中A、B两点的电压和电流代入得: E=16+0.2 r E=4+0.8 r 解得E=20 V,r=20 Ω. (2)当R3的滑片滑到最右端时,R3、R1均被短路,此时外电路电阻等于R2,且对应于图线上B点,故由B点的U、I值可求出R2的阻值为: R2== Ω=5 Ω. (3)滑动变阻器的滑片置于最左端时,R3阻值最大.设此时外电路总电阻为R,由图象中A点坐标求出: R== Ω=80 Ω. 又R=+R2,代入数值解得滑动变阻器的最大阻值R3=300 Ω. 5.如图所示,一台电动机提着质量为m的物体,以速度v匀速上升。已知电动机线圈的电阻为R,电源电动势为E,通过电源的电流为I,当地重力加速度为g,忽略一切阻力导线电阻,则( ) 5题图 A.电源内阻 B.电源内阻 C.如果电动机转轴被卡住而停止转动,较短时间内电源消耗的功率将变大 D.如果电动机转轴被卡住而停止转动,较短时间[内电源消耗的功率将变小 【答案】BC 6.如右图所示,曲线C1、C2分别是纯电阻直流电路中,内、外电路消耗的电功率随电流变化的图线.由该图可知下列说法中错误的是 6图 A.电源的电动势为4V B.电源的内电阻为1Ω C.电源输出功率最大值为8W D.电源被短路时,电源消耗的最大功率可达16W 【答案】C 7.如图所示,直线Ⅰ、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的特性图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,如果把该小灯泡先后分别与电源1和电源2单独连接时,则下列说法不正确的是 7图 A.电源1和电源2的内阻之比是11∶7 B.电源1和电源2的电动势之比是1∶1 C.在这两种连接状态下,小灯泡消耗的功率之比是1∶2 D.在这两种连接状态下,小灯泡的电阻之比是1∶2 【答案】D 【解析】:电源U-I图线斜率的绝对值表示电源内阻、纵截距等于电源电动势,AB皆正确。小灯泡U-I图线与电源U-I图线的交点坐标线所围成矩形面积表示该连接状态下电源的输出功率也即小灯泡消耗的功率,可知C正确;交点与坐标原点连线的斜率表示该状态下电源外电路电阻即小灯泡电阻,由图知应为18:25,D错误。 8.和蓓同 用常规器材研究标有“2.5V 0.3A”字样的小灯泡两端的电压和通过其电流的关系,先选择合理的电路再正确连线,闭合开关进行实验,得到的数据如下表所示. 次数 1 2 3 4 5 6 7 8 9 10 电压U/V 0 0.10 0.20 0.40 0.60 1.00 1.60 1.80 2.20 2.50 电流I/A 0 0.08 0.14 0.18 0.19 0.22 0.26 0.28 0.30 0.32 (1)在甲图虚线框内画出实验电路图(图中电源和开关已画好) 2图 (2)在乙图坐标系中,选取适当的标度,画出小灯泡的U—I图线 (3)经分析可得出:当小灯泡中电流为零时,电阻约为 Ω,当U=2.00V时,电阻约为 Ω,其阻值不同的原因是 。 (4)若将该灯泡与阻值为l0Ω的电阻串联后接在电动势E=3V、内阻不计的电源两端,则小灯泡实际消耗的功率约为 W。 2答图 【答案】 (1)如图甲(2)如图乙(3)1.25 6.9(6.5 7.2)灯泡电阻随温度升高而增大 (4)0.176(0.16 0.22) (4)设此时灯泡两端电压为U,通过的电流为I,由闭合电路的欧姆定律有即U=3-10I,在测得的灯泡的U-I图象中作出此函数关系图线,如图丙,可从两图线的交点得到电路中的电压与电流分别为U=0.85V,I=0.21A,则消耗的功率为P=IU=0.179W.查看更多