【物理】2020届一轮复习人教版专题二处理平衡问题的几种方法学案

【物理】2020届一轮复习人教版专题二处理平衡问题的几种方法学案

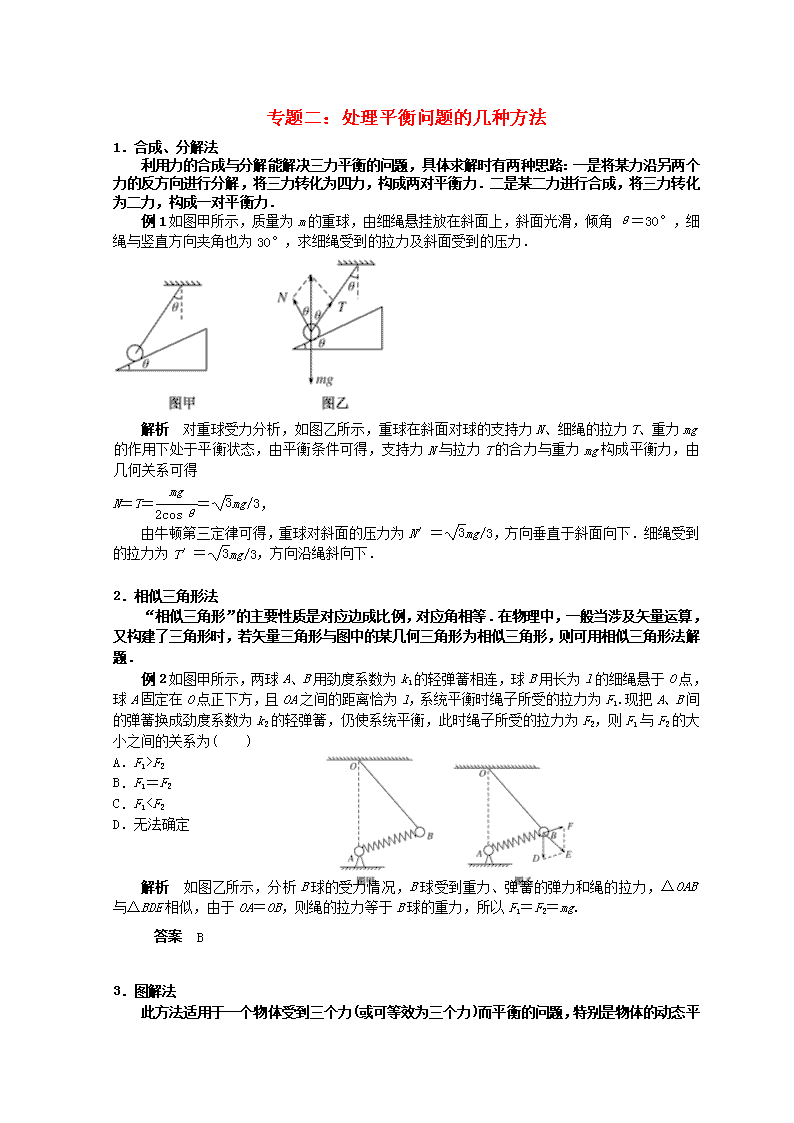
专题二：处理平衡问题的几种方法 ‎1．合成、分解法 利用力的合成与分解能解决三力平衡的问题，具体求解时有两种思路：一是将某力沿另两个力的反方向进行分解，将三力转化为四力，构成两对平衡力．二是某二力进行合成，将三力转化为二力，构成一对平衡力．‎ 例1如图甲所示，质量为m的重球，由细绳悬挂放在斜面上，斜面光滑，倾角θ＝30°，细绳与竖直方向夹角也为30°，求细绳受到的拉力及斜面受到的压力．‎ 解析　对重球受力分析，如图乙所示，重球在斜面对球的支持力N、细绳的拉力T、重力mg的作用下处于平衡状态，由平衡条件可得，支持力N与拉力T的合力与重力mg构成平衡力，由几何关系可得 N＝T＝＝mg/3，‎ 由牛顿第三定律可得，重球对斜面的压力为N′＝mg/3，方向垂直于斜面向下．细绳受到的拉力为T′＝mg/3，方向沿绳斜向下．‎ ‎2．相似三角形法 ‎“相似三角形”的主要性质是对应边成比例，对应角相等．在物理中，一般当涉及矢量运算，又构建了三角形时，若矢量三角形与图中的某几何三角形为相似三角形，则可用相似三角形法解题．‎ 例2如图甲所示，两球A、B用劲度系数为k1的轻弹簧相连，球B用长为l的细绳悬于O点，球A固定在O点正下方，且OA之间的距离恰为l，系统平衡时绳子所受的拉力为F1.现把A、B间的弹簧换成劲度系数为k2的轻弹簧，仍使系统平衡，此时绳子所受的拉力为F2，则F1与F2的大小之间的关系为(　　)‎ A．F1>F2 ‎ B．F1＝F2‎ C．F1f′Bcosθ，f′B＝fB＝μNB，即μμmgcosθ，物体B的加速度方向一定沿斜面向下，A正确；若只撤去F1，N″B＝mgcosθ，f″B＝μmgcosθf″Bcosθ，A所受地面摩擦力方向仍向左，B错；若只撤去F2，A所受地面摩擦力方向向左不变，C错D对．‎ 答案　AD 规律总结　‎ ‎(1)物体或系统受四个或四个以上作用力时，一般采用正交分解法求解．‎ ‎(2)当物体或系统受力发生变化，在比较变化前、后的受力或运动情况时，要分清不变力和变化力，抓住变化力或者变化力的某方向上的分量进行比较，可以简化运算过程；如上题中，要求讨论斜劈A所受地面摩擦力的变化，只要抓住斜劈A所受变化力中的水平分力进行比较，就能较快地得出结论．‎ ‎(3)要善于转换研究对象．选择研究对象时优先整体也是相对的，当整体法有困难时一定记得要选择恰当的隔离体作研究对象．‎ ‎5．正弦定理法 三力平衡时，三力的合力为0，三个力可构成一封闭三角形，若由题设条件寻找到角度关系，则可用正弦定理列式求解．‎ 例5一盏电灯重力为G，悬于天花板上A点，在电线O处系一细线OB，使电线OA与竖直方向的夹角为β＝30°，如图甲所示．现保持β角不变，缓慢调整OB方向至OB线上拉力最小为止，此时OB与水平方向的夹角α等于多少？最小拉力是多少？‎ 解析　‎ 对电灯受力分析如图乙所示，据三力平衡特点可知：OA、OB对O点的作用力TA、TB的合力T与G等大反向，即T＝G①‎ 在△OTBT中，∠TOTB＝90°－α，‎ 又∠OTTB＝∠TOA＝β，故∠OTBT＝180°－(90°－α)－β＝90°＋α－β，‎ 由正弦定理得＝②‎ 联立解得TB＝，‎ 因β不变，故当α＝β＝30°时，TB最小，且TB＝Gsinβ＝G/2‎ ‎6．整体法和隔离法 选择研究对象是解决物理问题的首要环节．若一个系统中涉及两个或者两个以上物体的平衡问题，在选取研究对象时，要灵活运用整体法和隔离法．对于多物体问题，如果不求物体间的相互作用力，我们优先采用整体法，这样涉及的研究对象少，未知量少，方程少，求解简便；很多情况下，通常采用整体法和隔离法相结合的方法．‎ 例6如图所示，顶端装有定滑轮的斜面体放在粗糙水平面上，A、B两物体通过细绳相连，并处于静止状态(不计绳的质量和绳与滑轮间的摩擦)．现用水平向右的力F作用于物体B上，将物体B缓慢拉高一定的距离，此过程中斜面体与物体A仍然保持静止．在此过程中(　　)‎ A．水平力F一定变小 B．斜面体所受地面的支持力一定变大 C．物体A所受斜面体的摩擦力一定变大 D．地面对斜面体的摩擦力一定变大 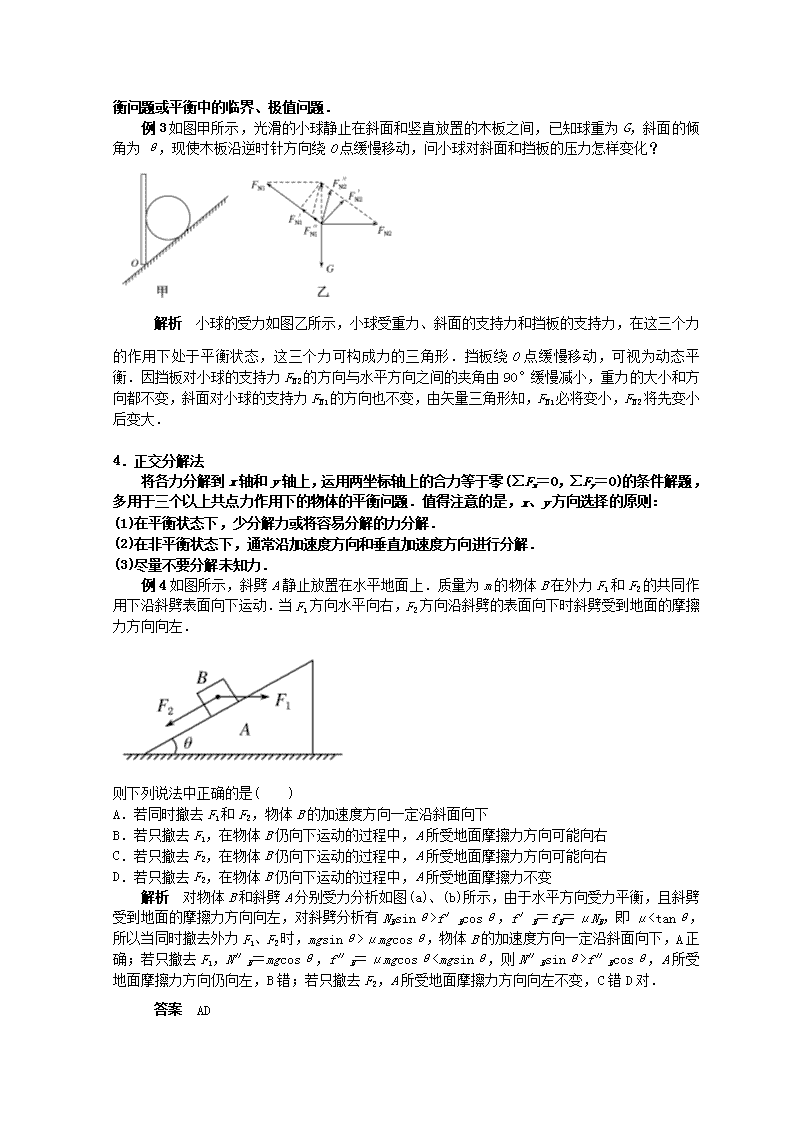解析　隔离物体B为研究对象，分析其受力情况如图所示．‎ 则有F＝mgtanθ，T＝，在物体B缓慢拉高的过程中，θ增大，则水平力F随之变大，对A、B两物体与斜面体这个整体而言，由于斜面体与物体A仍然保持静止，则地面对斜面体的摩擦力一定变大，但是因为整体竖直方向并没有其他力，故斜面体所受地面的支持力不变；在这个过程中尽管绳子张力变大，但是由于物体A所受斜面体的摩擦力开始并不知道其方向，故物体A所受斜面体的摩擦力的情况无法确定，所以答案为D.‎ ‎7．平衡问题中极值的求法 极值是指研究平衡问题中某物理量变化时出现的最大值或最小值．中学物理的极值问题可分为简单极值问题和条件极值问题，区分的依据是是否受附加条件制约．若受附加条件制约，则为条件极值．‎ 例7如图所示，物体放在水平面上，与水平面间的动摩擦因数为μ，现施一与水平面成α角且斜向下的力F推物体，问：α至少为多大时，F无论多大均不能推动物体(设最大静摩擦力等于滑动摩擦力)?‎ 解析　设物体的质量为m，静摩擦力为Ff，现取刚好达到最大静摩擦力时分析，如图，由平衡条件有Fcosα＝μ(mg＋Fsinα)，即F＝.‎ 上式中出现三个未知量，缺少条件，但注意到题中“无论F多大……”，可设想：当F→∞时，必有右边分式的分母→0，即cosα－μsinα＝0，得α ‎＝arctan，因此α≥arctan，即为所求．‎ 答案　α≥arctan 规律总结　‎ 注意到题中“无论F多大……”，可设想：当F→∞时，必有右边分式的分母→0.‎