2019届二轮复习12带电粒子在复合场中的运动问题课件(46张)
第
12
讲 带电粒子在复合场
中
的
运动问题
-
2
-
带电粒子在组合场中的运动
考向
1
磁场
+
磁场
【典题
1
】
(2018
年
2
月宁波期末
,22)
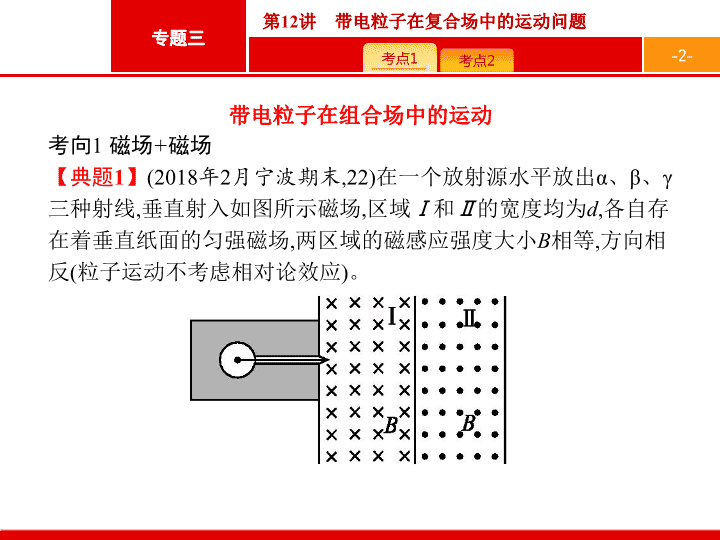
在一个放射源水平放出
α
、
β
、
γ
三种射线
,
垂直射入如图所示磁场
,
区域
Ⅰ
和
Ⅱ
的宽度均为
d
,
各自存在着垂直纸面的匀强磁场
,
两区域的磁感应强度大小
B
相等
,
方向相反
(
粒子运动不考虑相对论效应
)
。
-
3
-
(1)
若要筛选出速率大小
v
1
的所有
β
粒子进入区域
Ⅱ
,
求磁场宽度
d
与
B
和
v
1
的关系
;
(2)
若
B=
0
.
027 3 T,
v
1
=
0
.
1
c
(
c
是光速度
),
计算
d
;
α
粒子的速率为
0
.
001
c
,
计算
α
粒子和
γ
射线离开区域
Ⅰ
时的距离
(
答案均保留三位有效数字
);
(3)
当
d
满足第
(1)
小题所给关系时
,
请给出速率在
v
1
v>
0
.
5
v
1
,
那么荧光屏发光的坐标范围是多少
?
-
10
-
解析
:
(1)
粒子进入磁场
Ⅱ
的最小速度情况如图
1
所示
:
图
1
由洛伦兹力提供向心力得
:
-
11
-
图
2
-
12
-
(3)
①
当
0
.
5
v
1
0)
的粒子以速度
v
从
O
点垂直于磁场方向射入磁场
,
当速度方向沿
x
轴正方向时
,
粒子恰好从
O
1
(
x=a
的位置
)
点正上方的
A
点沿
y
轴正方向射出磁场
,
不计粒子重力。
-
33
-
(1)
求磁感应强度
B
的大小。
(2)
若粒子以速度
v
从
O
点垂直于磁场方向射入磁场
,
速度方向沿
x
轴正方向成
θ
角
(
-
90
°
<
θ
<
90
°
,
其中粒子射入第一象限
,
θ
取正
;
粒子射入第四象限
,
θ
取负
),
为使这些粒子射出磁场后在电场中运动的时间相同且最长
,
写出磁场边界的轨迹方程。
(3)
磁场的边界如题
(2)
所求
,
若粒子以速度
v
从
O
点垂直于磁场方向射入第一象限
,
当速度方向沿
x
轴正方向的夹角
θ
=
30
°
时
,
求粒子从射入磁场到最终离开磁场的总时间
t
。
解析
:
(1)
由题知该粒子在磁场中运动的轨迹半径
r=a
,
-
34
-
(2)
要使这些粒子射出磁场后能在电场中运动的时间相同且最长
,
则要求进入电场时的速度与电场线平行。设与
y
轴正方向成
θ
角的粒子从磁场边界某点
P
(
x
,
y
)
射出
,
由题知粒子运动轨迹对应的圆心角刚好为
θ
1
=
90
°
-
θ
,
如图所示
,
由几何关系得
P
点坐标为
x=a
(1
-
cos
θ
1
),
y=a
sin
θ
1
,
消去
θ
1
得
,
边界曲线的方程
为
(
x-a
)
2
+y
2
=a
2
,
即所加磁场在以
(
a
,0)
为圆心
,
半径
为
a
的圆内
,
如
图中圆所示。
-
35
-
粒子从磁场中的
P
点射出
,
因磁场圆和粒子的轨迹圆的半径相等
,
OO
1
PO
2
构成菱形
,
故粒子从
P
点的出射方向与
y
轴平行
,
粒子由
O
到
P
所对应的圆心角为
θ
1
=
60
°
由几何知识可知
,
粒子由
P
点到
x
轴的距离
s=a
cos
θ
粒子在电场中做匀变速运动
,
在电场中运动的时间
粒子由
P
点第
2
次进入磁场
,
由
Q
点射出
,
PO
1
QO
3
构成菱形
,
由几何知识可知
Q
点在
x
轴上
,
粒子由
P
到
Q
的偏向角为
θ
2
=
120
°
则
θ
1
+
θ
2
=
π
-
36
-
-
37
-
带电粒子在叠加场中的运动
【典题
4
】
(2017
浙江绍兴三月模拟
)
质谱仪由电离室、加速区、速度选择器和磁分析区
(
图中未画出
)
组成。电离室会电离出速度不同的同种带电粒子
,
加速区电压为
U
,
速度选择器中电场强度方向向下
,
大小为
E
,
磁场垂直纸面向内
,
B
的大小可变化。
O
1
,
O
,
O
2
三个小孔在同一直线上
,
且平行于选择器极板。
-
38
-
(1)
当电离室的带电粒子速度几乎为零由
O
1
“
飘出
”,
调节磁感应强度为
B
1
时
,
从小孔
O
点进入的粒子可以直线通过选择器
,
求该带电粒子的
比荷
。
(2)
某研究员发现
,
当电离室中
“
飘出
”
带电粒子的速度值处于
0
~v
0
之间
,
控制选择器的磁感应强度在
B
0
~B
1
(
B
0
查看更多