【物理】2019届一轮复习人教版　习题课：气体实验定律和理想气体状态方程的应用学案

【物理】2019届一轮复习人教版　习题课：气体实验定律和理想气体状态方程的应用学案

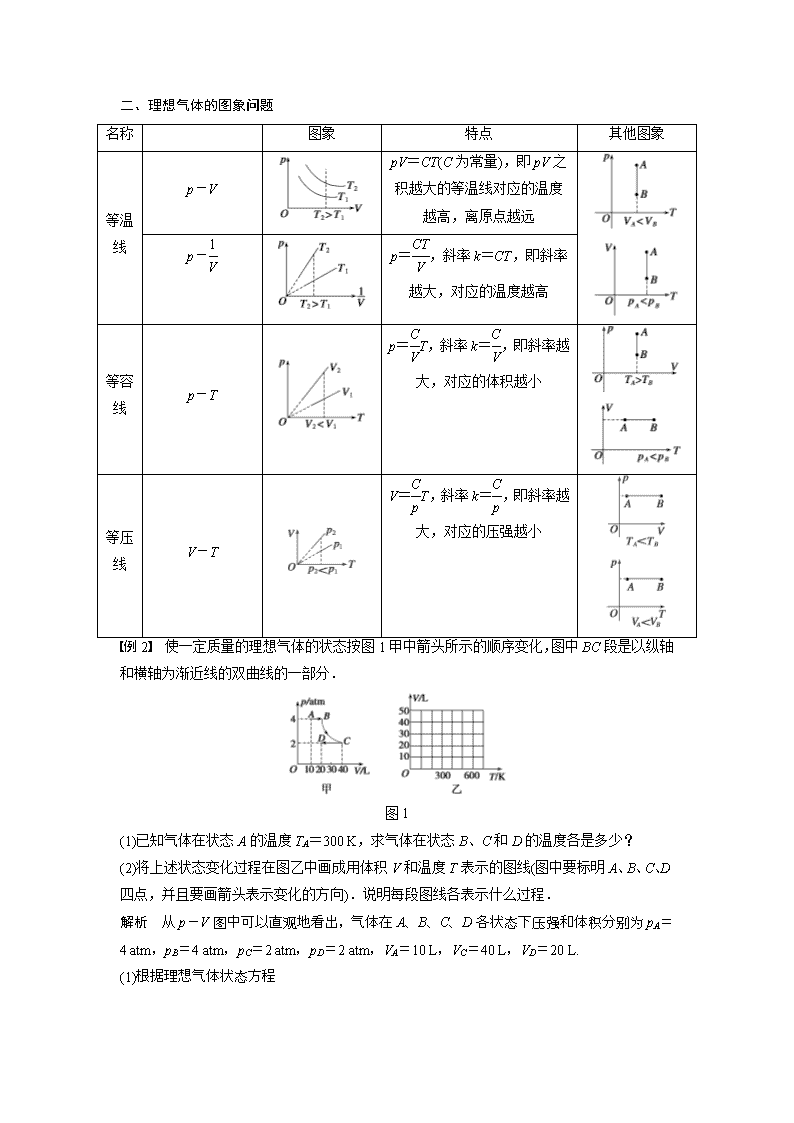
学案 4 习题课：气体实验定律和理想气体状态方程的应用 [考纲定位] 1.会巧妙地选择研究对象，使变质量问题转化为一定质量的气体问题.2.会利用图 象对气体状态、状态变化及规律进行分析，并应用于解决气体状态变化问题.3.会应用气体实 验定律和理想气体状态方程解决综合问题． 一、变质量问题 分析变质量问题时，可以通过巧妙选择合适的研究对象，使这类问题转化为定质量的气体问 题，从而用气体实验定律或理想气体状态方程解决．以常见的两类问题举例说明： 1．打气问题 向球、轮胎中充气是一个典型的变质量的气体问题．只要选择球内原有气体和即将打入的气 体作为研究对象，就可把充气过程看成等温压缩过程． 2．抽气问题 从容器内抽气的过程中，容器内的气体质量不断减小，这属于变质量问题．分析时，将每次 抽气过程中抽出的气体和剩余气体作为研究对象，总质量不变，故抽气过程可看成是等温膨 胀过程． 例 1 氧气瓶的容积是 40 L，其中氧气的压强是 130 atm，规定瓶内氧气压强降到 10 atm 时就要重新充氧．有一个车间，每天需要用 1 atm 的氧气 400 L，这瓶氧气能用几天？假定 温度不变． 解析 用如图所示的方框图表示思路． 由 V1→V2：p1V1＝p2V2， V2＝p1V1 p2 ＝130×40 10 L＝520 L， 由(V2－V1)→V3：p2(V2－V1)＝p3V3， V3＝p2V2－V1 p3 ＝10×480 1 L＝4 800 L， 则 V3 400 L ＝12(天)． 答案 12 天 二、理想气体的图象问题 名称 图象 特点 其他图象 等温 线 p－V pV＝CT(C 为常量)，即 pV 之 积越大的等温线对应的温度 越高，离原点越远 p－1 V p＝CT V ，斜率 k＝CT，即斜率 越大，对应的温度越高 等容 线 p－T p＝C VT，斜率 k＝C V ，即斜率越 大，对应的体积越小 等压 线 V－T V＝C pT，斜率 k＝C p ，即斜率越 大，对应的压强越小 例 2 使一定质量的理想气体的状态按图 1 甲中箭头所示的顺序变化，图中 BC 段是以纵轴 和横轴为渐近线的双曲线的一部分． 图 1 (1)已知气体在状态 A 的温度 TA＝300 K，求气体在状态 B、C 和 D 的温度各是多少？ (2)将上述状态变化过程在图乙中画成用体积 V 和温度 T 表示的图线(图中要标明 A、B、C、 D 四点，并且要画箭头表示变化的方向)．说明每段图线各表示什么过程． 解析 从 p－V 图中可以直观地看出，气体在 A、B、C、D 各状态下压强和体积分别为 pA ＝4 atm，pB＝4 atm，pC＝2 atm，pD＝2 atm，VA＝10 L，VC＝40 L，VD＝20 L. (1)根据理想气体状态方程 pAVA TA ＝pCVC TC ＝pDVD TD ， 可得 TC＝pCVC pAVA ·TA＝2×40 4×10 ×300 K＝600 K， TD＝pDVD pAVA ·TA＝2×20 4×10 ×300 K＝300 K， 由题意知 B 到 C 是等温变化，所以 TB＝TC＝600 K. (2)由状态 B 到状态 C 为等温变化， 由玻意耳定律有 pBVB＝pCVC，得 VB＝pCVC pB ＝2×40 4 L＝20 L. 在 V－T 图上状态变化过程的图线由 A、B、C、D 各状态依次连接(如图)，AB 是等压膨胀过 程，BC 是等温膨胀过程，CD 是等压压缩过程． 答案 (1)600 K 600 K 300 K (2)见解析 三、理想气体的综合问题 1．定性分析液柱移动问题： 定性分析液柱移动问题常使用假设推理法：根据题设条件，假设液柱不动，运用相应的物理 规律及有关知识进行严谨的推理，得出正确的答案． 常用推论有两个： (1)查理定律的分比形式：Δp ΔT ＝p T 或Δp＝ΔT T p. (2)盖—吕萨克定律的分比形式：ΔV ΔT ＝V T 或ΔV＝ΔT T V. 2．定量计算问题： 定量计算问题是热学部分的典型的物理综合题，它需要考查气体、气缸或活塞等多个研究对 象，涉及热学、力学等物理知识，需要灵活、综合地应用知识来解决问题． 解决该问题的一般思路： (1)弄清题意，确定研究对象． (2)分析清楚初、末状态及状态变化过程，依据气体实验定律列出方程；对力学研究对象要 正确地进行受力分析，依据力学规律列出方程进而求出压强． (3)注意挖掘题目中的隐含条件，如几何关系等，列出辅助方程． (4)多个方程联立求解．对求解的结果注意检验它们的合理性． 例 3 如图 3 所示，固定的绝热气缸内有一质量为 m 的 T 型绝热活塞(体积可忽略)，距气 缸底部 h0 处连接一 U 形管(管内气体的体积忽略不计)．初始时，封闭气体温度为 T0，活塞 距离气缸底部为 1.5h0，两边水银柱存在高度差．已知水银的密度为ρ，大气压强为 p0，气缸 横截面积为 S，活塞竖直部分长为 1.2h0，重力加速度为 g，试问： 图 3 (1)初始时，水银柱两液面高度差多大？ (2)缓慢降低气体温度，水银柱两液面相平时温度是多少？ 答案 (1)m ρS (2) 4p0T0S 5p0S＋5mg 解析 (1)被封闭气体压强 p＝p0＋mg S ＝p0＋ρgh 初始时，水银柱两液面高度差为 h＝m ρS. (2)降低温度直至水银柱两液面相平的过程中，气体先等压变化，后等容变化． 初状态：p1＝p0＋mg S ，V1＝1.5h0S，T1＝T0 末状态：p2＝p0，V2＝1.2h0S，T2＝？ 根据理想气体状态方程p1V1 T1 ＝p2V2 T2 ， 代入数据得：T2＝ 4p0T0S 5p0S＋5mg 1. (变质量问题)某种喷雾器的贮液筒的总容积为 7.5 L，如图 4 所示，装入 6 L 的药液后再用 密封盖将贮液筒密封，与贮液筒相连的活塞式打气筒每次能压入 300 cm3、1 atm 的空气，设 整个过程温度保持不变，求： 图 4 (1)要使贮液筒中空气的压强达到 4 atm，打气筒应打压几次？ (2)在贮液筒中空气的压强达到 4 atm 时，打开喷嘴使其喷雾，直到内外气体压强相等，这时 筒内还剩多少药液？ 答案 (1)15 (2)1.5 L 解析 (1)设每打一次气，贮液筒内增加的压强为 p 由玻意耳定律得：1 atm×300 cm3＝1.5×103 cm3×p，p＝0.2 atm 需打气次数 n＝4－1 0.2 ＝15 (2)设停止喷雾时贮液筒内气体体积为 V 由玻意耳定律得：4 atm×1.5 L＝1 atm×V V＝6 L 故还剩药液 7.5 L－6 L＝1.5 L. 2. (理想气体的图象问题)一定质量的理想气体，经历一膨胀过程，此过程可以用图 5 中的直 线 ABC 来表示，在 A、B、C 三个状态上，气体的温度 TA、TB、TC 相比较，大小关系为( ) 图 5 A．TB＝TA＝TC B．TA＞TB＞TC C．TB＞TA＝TC D．TB＜TA＝TC 答案 C 解析 由题图中各状态的压强和体积的值：pAVA＝pCVC＜pBVB，因为pV T ＝C，可知 TA＝TC＜ TB. 3．(液体移动问题)两端封闭、内径均匀的直玻璃管水平放置，如图 6 所示．V 左Δp 左，即右侧压强降低得比左侧多，故水银柱向右移动，选项 C 正确． 4．(液体移动问题)如图 7 所示，A 气缸横截面积为 500 cm2，A、B 两个气缸中装有体积均为 10 L、压强均为 1 atm、温度均为 27 ℃的理想气体，中间用细管连接．细管中有一绝热活塞 M，细管容积不计．现给左边的活塞 N 施加一个推力，使其缓慢向右移动，同时给 B 中气 体加热，使此过程中 A 气缸中的气体温度保持不变，活塞 M 保持在原位置不动．不计活塞 与器壁、细管间的摩擦，周围大气压强为 1 atm＝105 Pa，当推力 F＝5 3 ×103 N 时，求： 图 7 (1)活塞 N 向右移动的距离是多少厘米？ (2)B 气缸中的气体升温到多少摄氏度？ 答案 (1)5 cm (2)127 ℃ 解析 (1)pA′＝pA＋F S ＝4 3 ×105 Pa 对 A 中气体，由 pAVA＝pA′VA′ 得 VA′＝pAVA pA′ ，解得 VA′＝3 4VA LA＝VA S ＝20 cm LA′＝VA′ S ＝15 cm Δx＝LA－LA′＝5 cm (2)对 B 中气体，pB′＝pA′＝4 3 ×105 Pa 由pB TB ＝pB′ TB′ ，解得 TB′＝pB′ pB TB＝400 K＝127 ℃. 题组一 变质量问题 1．空气压缩机的储气罐中储有 1.0 atm 的空气 6.0 L，现再充入 1.0 atm 的空气 9.0 L．设充 气过程为等温过程，空气可看做理想气体，则充气后储气罐中气体压强为( ) A．2.5 atm B．2.0 atm C．1.5 atm D．1.0 答案 A 解析 取全部气体为研究对象，由 p1V1＋p2V2＝pV1 得 p＝2.5 atm，故 A 正确． 2．用打气筒将压强为 1 atm 的空气打进自行车胎内，如果打气筒容积ΔV＝500 cm3，轮胎容 积 V＝3 L，原来压强 p＝1.5 atm.现要使轮胎内压强变为 p′＝4 atm，问用这个打气筒要打 气几次(设打气过程中空气的温度不变)( ) A．5 次 B．10 次 C．15 次 D．20 次 答案 C 解析 因为温度不变，可应用玻意耳定律的分态气态方程求解．pV＋np1ΔV＝p′V，代入数 据得 1．5 atm×3 L＋n×1 atm×0.5 L＝4 atm×3 L， 解得 n＝15. 故答案选 C. 3．容积为 5×10－3 m3 的容器内盛有理想气体，若用最大容积为 0.1×10－3 m3 的活塞抽气筒 抽气，在温度不变的情况下抽气 10 次，容器内剩余气体的压强是最初压强的多少倍？ 答案 0.82 解析 本题是一道变质量问题，我们必须转化成质量一定的问题．因为每次抽出的气体压强 不一样，但可把抽气等效成容器与真空的抽气筒相通，所以每次抽气可视为质量一定的气体 体积增大ΔV.设容器中原有气体的压强为 p0，体积为 V0，抽气筒容积为ΔV. 第一次抽气：p0V0＝p1(V0＋ΔV)， 第二次抽气：p1V0＝p2(V0＋ΔV)， 第三次抽气：p2V0＝p3(V0＋ΔV)， … 第十次抽气：p9V0＝p10(V0＋ΔV)， 各式相乘可得 p10＝( V0 V0＋ΔV)10p0. 所以p10 p0 ＝( V0 V0＋ΔV)10＝( 5 5＋0.1)10≈0.82. 题组二 理想气体的图象问题 4．在下列图中，不能反映一定质量的理想气体经历了等温变化→等容变化→等压变化后， 又回到初始状态的图是( ) 答案 D 解析 根据 p－V、p－T、V－T 图象的物理意义可以判断，其中 D 反映的是理想气体经历 了等温变化→等压变化→等容变化，与题意不符． 5.如图 1 所示，用活塞把一定质量的理想气体封闭在导热气缸中，用水平外力 F 作用于活塞 杆，使活塞缓慢向右移动，由状态①变化到状态②.如果环境保持恒温，分别用 p、V、T 表 示该理想气体的压强、体积、温度．气体从状态①变化到状态②，此过程可用下图中哪几个 图象表示( ) 图 1 答案 AD 解析 由题意知，由状态①到状态②过程中，温度不变，体积增大，根据pV T ＝C 可知压强将 减小．对 A 图象进行分析，p－V 图象是双曲线即等温线，且由状态①到状态②体积增大， 压强减小，故 A 项正确；对 B 图象进行分析，p－V 图象是直线，温度会发生变化，故 B 项 错误；对 C 图象进行分析，可知温度不变，但体积减小，故 C 项错误；对 D 图象进行分析， 可知温度不变，压强减小，故体积增大，D 项正确． 6．如图 2 所示为一定质量的理想气体沿着箭头所示的方向发生状态变化的过程，则该气体 压强的变化是( ) 图 2 A．从状态 c 到状态 d，压强减小 B．从状态 d 到状态 a，压强不变 C．从状态 a 到状态 b，压强增大 D．从状态 b 到状态 c，压强增大 答案 AC 解析 在 V－T 图上，等压线是延长线过原点的倾斜直线，对一定质量的理想气体，图线上 的点与原点连线的斜率表示压强的倒数，即斜率大的，压强小，因此 A、C 正确，B、D 错 误． 7．如图 3 所示是理想气体经历的两个状态变化的 p－T 图象，对应的 p－V 图象应是图中的 ( ) 图 3 答案 C 题组三 理想气体的综合问题 8．如图所示，四个两端封闭、粗细均匀的玻璃管内的空气被一段水银柱隔开，按图中标明 的条件，当玻璃管水平放置时，水银柱处于静止状态．如果管内两端的空气都升高相同的温 度，则水银柱向左移动的是( ) 答案 CD 解析 假设升温后，水银柱不动，则两边压强都要增加，由查理定律有，压强的增加量Δp ＝pΔT T ，而各管原压强相同，ΔT 相同，所以Δp∞1 T ，即 T 高，Δp 小，也就可以确定水银柱 应向温度高的方向移动，故 C、D 项正确． 9．图 4 为一定质量理想气体的压强 p 与体积 V 的关系图象，它由状态 A 经等容过程到状态 B，再经等压过程到状态 C.设 A、B、C 状态对应的温度分别为 TA、TB、TC，则下列关系式 中正确的是( ) 图 4 A．TATB，TB＝TC C．TA>TB，TBTC 答案 C 解析 由题图可知，气体由 A 到 B 的过程为等容变化，由查理定律得pA TA ＝pB TB ，pA>pB，故 TA>TB； 由 B 到 C 的过程为等压变化，由盖—吕萨克定律得VB TB ＝VC TC ，VB

查看更多