人教版必修二5.6《向心力》WORD教案11

人教版必修二5.6《向心力》WORD教案11

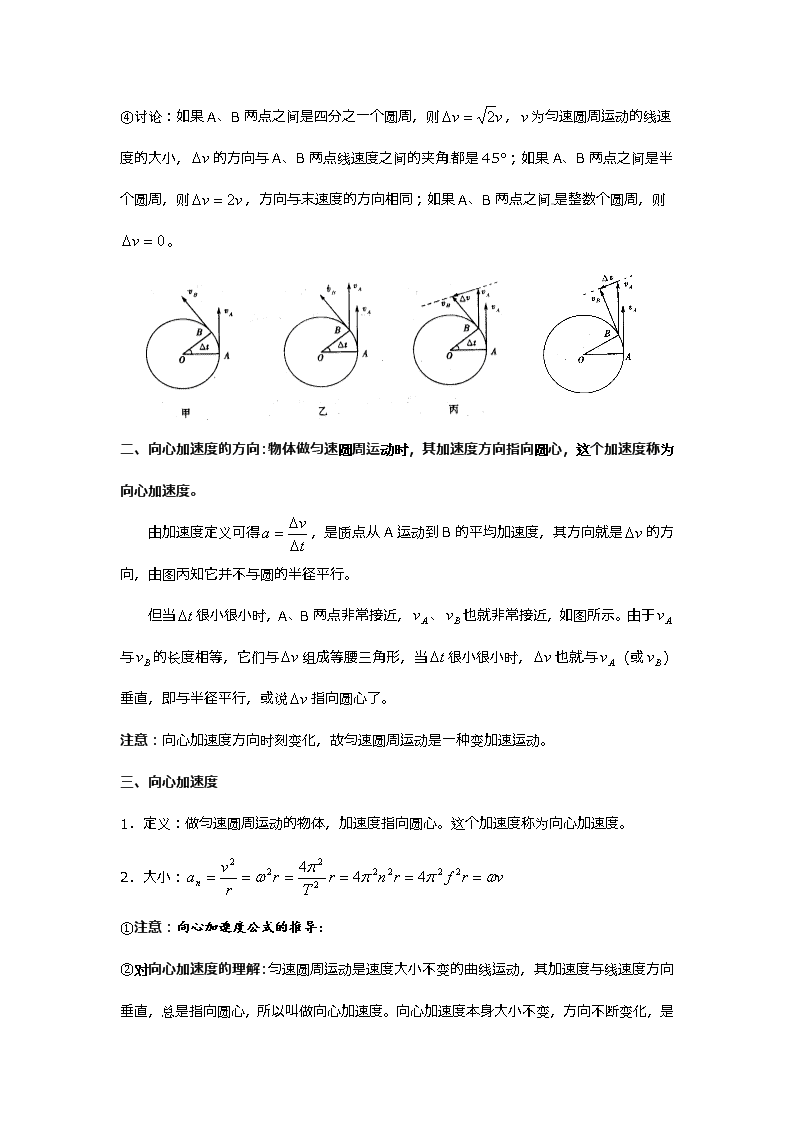
向心加速度 一、速度变化量 ‎1.速度的变化量 在一段时间内，运动物体的末速度减去初速度就是这个物体在这段时间内(或这一过程中)的速度的变化量。‎ ‎ 重要的是，速度的矢量，末速度减去初速度是矢量减法，要采用平行四边形法则，而不是同学们所习惯的代数减法，这正是难点所在。理解并掌握速度的变化量对以后学习动量定理有直接而重大的意义，因此也是学习的重点内容。‎ ‎2.同一直线上速度的变化量 如果初速度和末速度在同一条直线上，速度的变化量可以简化为代数运算。设初速度为，末速度为，速度的变化量为，把这两个速度矢量的起点画到同一点上。‎ 关于速度变化量的几种情形：[来源:学#科#网Z#X#X#K]‎ ‎①初速度和末速度方向相同，末速度大于初速度，此时速度的变化量与初、末速度的方向相同，大小等于末速度的大小减去初速度的大小，如图所示。‎ 例如：物体初速度向西，大小为‎3m/s，经过一段时间后，末速度也向西，大小为‎8m/s，则速度的变化量大小为‎5m/s，方向向西。‎ ‎②初速度和末速度方向相同，末速度小于初速度，此时速度的变化量与初、末速度的方向相反，大小等于初速度的大小减去末速度的大小，如图所示。‎ 例如：物体初速度向西，大小为‎8m/s，经过一段时间后，末速度也向西，大小为‎3m/s，则速度的变化量大小为‎5m/s，方向向东。‎ ‎③初速度和末速度方向相反，这时不管是初速度大，还是末速度大，速度的变化量总与末速度的方向相同，大小等于末速度的大小加上初速度的大小，如图所示。 ‎ 例如：物体初速度向东，大小为‎3m/s，经过一段时间后，末速度向西，大小为‎5m/s，则速度的变化量大小为‎8m/s，方向向西。‎ 结论：从同一点作出物体在一段时间的始末两个速度矢量和，从初速度矢量的末端作出一个矢量到末速度矢量的末端，所作的矢量就等于速度的变化量。‎ ‎3.不在同一条直线上的速度的变化量 上述结论对不在同一条直线上的速度的变化量仍然适用，即从同一点作出初速度矢量和末速度矢量，初速度矢量的末端到末速度矢量的末端作出的矢量就是速度的变化量，如图所示。‎ 例如：平抛运动，物体以初速度平抛，经一段时间后(物体未落地)，末速度方向沿轨迹的切线方向，其速度的变化量方向竖直向下。‎ ‎【例一】设物体在A点的初速度为，经过一段时间运动到B，末速度为，如图所示，‎ 用作图法分别求出物体在这段时间内的速度变化量。[来源:Z_xx_k.Com]‎ ‎4.匀速圆周运动物体在一段时间内速度的变化量 ‎①在匀速圆周运动中，物体由A运动到B，分别作出物体在A、B两点的速度矢量和，如图甲所示。由于是匀速圆周运动，和的长度是一样的。‎ ‎②为便于对和做比较，将的起点移到B点，同时保持的长度和方向不变，如图乙所示，它仍可代表质点在A处的速度。‎ ‎③以的箭头端为起点，的箭头端为终点作矢量，如图丙所示。如前所述，就是质点由A运动到B的速度的变化量。‎ ‎④讨论：如果A、B两点之间是四分之一个圆周，则，为匀速圆周运动的线速度的大小，的方向与A、B两点线速度之间的夹角都是45°；如果A、B两点之间是半个圆周，则，方向与末速度的方向相同；如果A、B两点之间是整数个圆周，则。‎ 二、向心加速度的方向：物体做匀速圆周运动时，其加速度方向指向圆心，这个加速度称为向心加速度。[来源:Z_xx_k.Com]‎ 由加速度定义可得，是质点从A运动到B的平均加速度，其方向就是的方向，由图丙知它并不与圆的半径平行。‎ 但当很小很小时，A、B两点非常接近，、也就非常接近，如图所示。由于与的长度相等，它们与组成等腰三角形，当很小很小时，也就与 (或)垂直，即与半径平行，或说指向圆心了。‎ 注意：向心加速度方向时刻变化，故匀速圆周运动是一种变加速运动。‎ 三、向心加速度 ‎1．定义：做匀速圆周运动的物体，加速度指向圆心。这个加速度称为向心加速度。‎ ‎2．大小： ‎ ‎①注意：向心加速度公式的推导：‎ ‎②对向心加速度的理解：匀速圆周运动是速度大小不变的曲线运动，其加速度与线速度方向垂直，总是指向圆心，所以叫做向心加速度。向心加速度本身大小不变，方向不断变化，是 不断变化的矢量。它不改变线速度的大小，但不断改变线速度的方向，使线速度总是沿着圆周的切线方向。如果线速度越大，不断改变线速度的方向需要的向心加速度也就越大；半径越大，不断改变线速度的方向需要的向心加速度越小，所以，线速度越大、半径越小，向心加速度就越大。[来源:Z+xx+k.Com]‎ ‎3．方向：总是沿着圆周运动半径指向圆心，始终与线速度方向垂直。‎ ‎4．意义：描述由于运动方向改变而引起的速度变化的快慢。‎ ‎5．匀速圆周运动是加速度变化的变加速曲线运动(非匀变速曲线运动)。因为对某一确定的匀速圆周运动来说，m、r、v、ω、T的大小都是不变的，所以向心力和向心加速度的大小不变，但方向却时刻改变。‎ ‎6．向心加速度公式也适用于非匀速圆周运动。对于变速率圆周运动，可以用公式求质点在圆周上某点的向心加速度瞬时值，其中w或v应取该点的线速度和角速度的瞬时值。‎ 向心加速度不一定是物体做圆周运动的实际加速度。对于匀速圆周运动，其所受的合外力就是向心力，只产生向心加速度，因而匀速圆周运动的向心加速度是其实际加速度，对于非匀速圆周运动，例如竖直平面内的圆周运动。如图，小球的合力不指向圆心，因而其实际加速度也不指向圆心，此时的向心加速度只是它的一个分加速度。‎ ‎【例二】关于质点做匀速圆周运动，下列说法中正确的是( )‎ A．线速度大，加速度一定大。‎ B．角速度大，加速度一定大。‎ C．周期大，加速度一定大。‎ D．加速度大，速度一定变化快。‎ ‎【例三】由于地球的自转，地球表面上各点均做匀速圆周运动，所以（ ）‎ A．地球表面各处具有相同大小的线速度。‎ B．地球表面各处具有相同大小的角速度。‎ C．地球表面各处具有相同大小的向心加速度。‎ D．地球表面各处的向心加速度方向都指向地球的球心。‎ ‎【例四】如图所示，为A、B两质点做匀速圆周运动的向心加速度随半径变化的图象，其中A为双曲线的一个分支。由图可知 ( )‎ A．A质点运动的线速度大小不变。‎ B．A质点运动的角速度大小不变。‎ C．B质点运动的角速度大小不变。‎ D．B质点运动的线速度大小不变。‎ ‎【例五】一质点做半径为R的匀速圆周运动，它的加速度、角速度、线速度、周期分别为n、m、v、T，下列关系中正确的有( )‎ A． B. C. D.‎ ‎【例六】如图所示为一皮带传动装置，右轮的半径为r，a是它边缘上的一点，左侧为一轮轴，大轮的半径为4r，小轮的半径为2r，b点在小轮上，到小轮中心距离为r，c点和d点分别位小轮和大轮的边缘上，若在传动过程中，皮带不打滑，则( )‎ A．a点与b点的线速度大小相等。‎ B．a点与c点的角速度大小相等。‎ C．a点与d点的向心加速度大小相等。‎ D．a、b、c、d四点，加速度最小的是b点。‎ ‎【例七】如图所示的传动装置中，A、B两轮同轴转动。A、B、C三轮的半径大小的关系是RA=RC=2RB。当皮带不打滑时，三轮的角速度之比、三轮边缘的线速度大小之比、三轮边缘的向心加速度大小之比分别为多少?‎ ‎[来源:学*科*网Z*X*X*K]‎ ‎【例八】如图所示，为皮带传动的主动轮的轴心，轮半径为。为从动轮的轴心，轮半径为。为固定在从动轮上的小轮半径。已知=2，=1.5，A、B、C分别是3个轮边缘上的点，则质点A、B、C的向心加速度之比是(皮带不打滑) ( )‎ A．1:2:3 B．2:4:3 C．8:4:3 D．3:6:2‎ www.ks5u.com