【物理】2020届一轮复习人教版实验：探究弹力与弹簧伸长的关系课时作业

【物理】2020届一轮复习人教版实验：探究弹力与弹簧伸长的关系课时作业

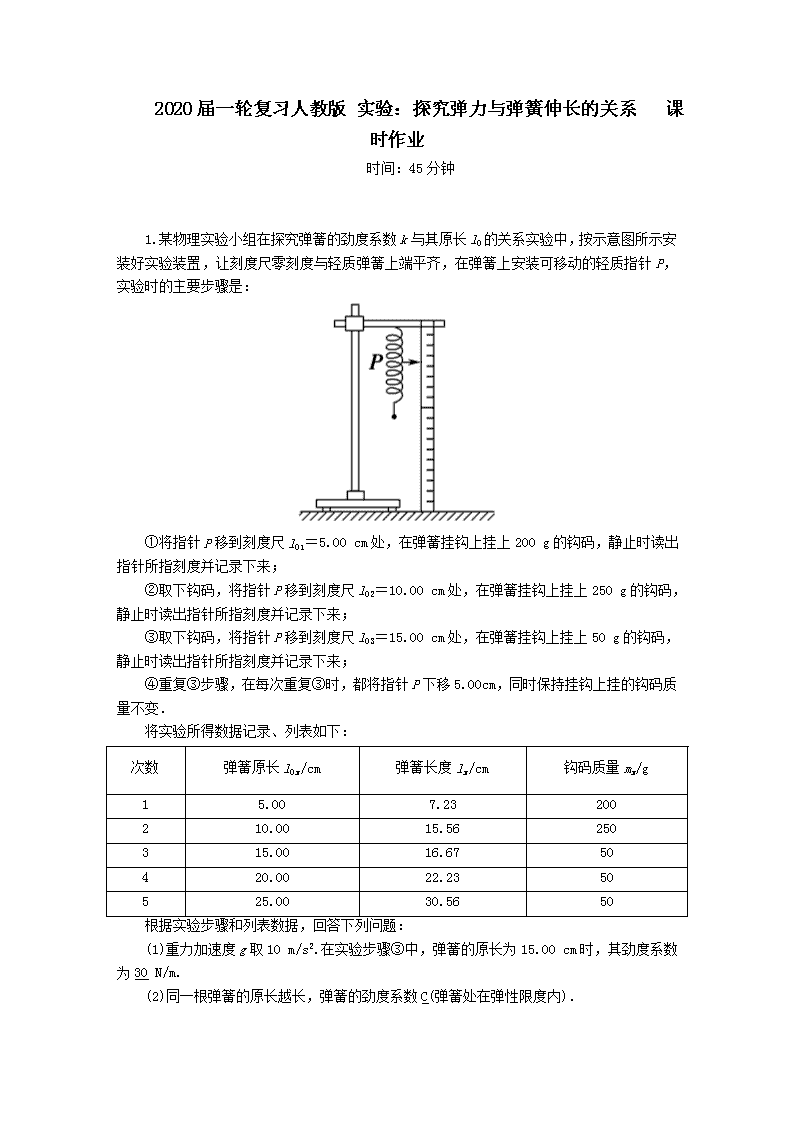
‎2020届一轮复习人教版 实验：探究弹力与弹簧伸长的关系 课时作业 时间：45分钟 ‎1.某物理实验小组在探究弹簧的劲度系数k与其原长l0的关系实验中，按示意图所示安装好实验装置，让刻度尺零刻度与轻质弹簧上端平齐，在弹簧上安装可移动的轻质指针P，实验时的主要步骤是：‎ ‎①将指针P移到刻度尺l01＝‎5.00 cm处，在弹簧挂钩上挂上‎200 g的钩码，静止时读出指针所指刻度并记录下来；‎ ‎②取下钩码，将指针P移到刻度尺l02＝‎10.00 cm处，在弹簧挂钩上挂上‎250 g的钩码，静止时读出指针所指刻度并记录下来；‎ ‎③取下钩码，将指针P移到刻度尺l03＝‎15.00 cm处，在弹簧挂钩上挂上‎50 g的钩码，静止时读出指针所指刻度并记录下来；‎ ‎④重复③步骤，在每次重复③时，都将指针P下移‎5.00 cm，同时保持挂钩上挂的钩码质量不变．‎ 将实验所得数据记录、列表如下：‎ 次数 弹簧原长l0x/cm 弹簧长度lx/cm 钩码质量mx/g ‎1‎ ‎5.00‎ ‎7.23‎ ‎200‎ ‎2‎ ‎10.00‎ ‎15.56‎ ‎250‎ ‎3‎ ‎15.00‎ ‎16.67‎ ‎50‎ ‎4‎ ‎20.00‎ ‎22.23‎ ‎50‎ ‎5‎ ‎25.00‎ ‎30.56‎ ‎50‎ 根据实验步骤和列表数据，回答下列问题：‎ ‎(1)重力加速度g取‎10 m/s2.在实验步骤③中，弹簧的原长为‎15.00 cm时，其劲度系数为30 N/m.‎ ‎(2)同一根弹簧的原长越长，弹簧的劲度系数C(弹簧处在弹性限度内)．‎ A．不变　　　B．越大　　　C．越小 解析：(1)弹簧的原长为l03＝‎15.00 cm时，挂钩上钩码的质量为m3＝‎50 g，所受拉力F3＝m‎3g＝0.5 N，弹簧长度l3＝‎16.67 cm，弹簧伸长Δx3＝l3－l03＝‎1.67 cm.根据胡克定律，F3＝k3Δx3，解得k3≈30 N/m.‎ ‎(2)弹簧的原长为l05＝‎25.00 cm时，挂钩上钩码的质量为m5＝‎50 g，所受拉力F5＝m‎5g＝0.5 N，弹簧长度l5＝‎30.56 cm，弹簧伸长Δx5＝l5－l05＝‎5.56 cm.根据胡克定律，F5＝k5Δx5，解得k5≈9 N/m.由此可知，同一根弹簧的原长越长，弹簧的劲度系数越小，选项C正确．‎ ‎2．图甲为某同学用力传感器去探究弹簧的弹力和伸长量的关系的实验情景．用力传感器竖直向下拉上端固定于铁架台的轻质弹簧，读出不同拉力下的标尺刻度x及拉力大小F(从电脑中直接读出)．所得数据记录在下列表格中：‎ 拉力大小F/N ‎0.45‎ ‎0.69‎ ‎0.93‎ ‎1.14‎ ‎1.44‎ ‎1.69‎ 标尺刻度x/cm ‎57.02‎ ‎58.01‎ ‎59.00‎ ‎60.00‎ ‎61.03‎ ‎62.00‎ ‎(1)从图乙读出刻度尺上的刻度值为63.60(63.58～63.62) cm；‎ ‎(2)根据所测数据，在图丙坐标纸上作出F与x的关系图象；‎ 答案：如图所示 ‎(3)由图象求出该弹簧的劲度系数24.8(24.6～25.0) N/m、弹簧的原长为55.2(55.1～55.3) cm.(均保留三位有效数字)‎ ‎3．某物理兴趣小组的同学在研究弹簧弹力的时候，测得弹力的大小F和弹簧长度L的关系如图1所示，则由图线可知：‎ ‎(1)弹簧的劲度系数为300_N/m.‎ ‎(2)为了用弹簧测定两木块A、B间的动摩擦因数μ，两同学分别设计了如图2所示的甲、乙两种方案．‎ ‎①为了用某一弹簧测力计的示数表示A和B之间的滑动摩擦力的大小，你认为方案甲更合理．‎ ‎②甲方案中，若A和B的重力分别为10.0 N和20.0 N．当A被拉动时，弹簧测力计a的示数为6.0 N，b的示数为11.0 N，则A、B间的动摩擦因数为0.3.‎ 解析：(1)由题图可知，当弹力为F0＝60 N，弹簧的伸长量x0＝L－L0＝‎20 cm＝‎0.2 m，由胡克定律得弹簧的劲度系数k＝＝ N/m＝300 N/m.‎ ‎(2)①甲、乙两种方案，在拉着A运动的过程中，拉A的弹簧测力计由于在不断地运动，示数可能会变化，读数不准，甲方案中的a是不动的，指针稳定，便于读数，甲方案更合理．②a的拉力与A对B的滑动摩擦力f平衡，由于a示数为6.0 N，即f＝F＝6.0 N，A、B 间的动摩擦因数μ＝＝＝0.3.‎ ‎4．(1)某次研究弹簧所受弹力F与弹簧长度L关系实验时，得到如图甲所示的FL图象，由图象可知：弹簧原长L0＝‎3.0 cm，求得弹簧的劲度系数k＝200 N/m.‎ ‎(2)按如图乙的方式挂上钩码(已知每个钩码重G＝1 N)，使(1)中研究的弹簧压缩，稳定后指针指示如图乙，则指针所指刻度尺示数为‎1.50 cm.由此可推测图乙中所挂钩码的个数为3个．‎ 解析：(1)由胡克定律F＝k(L－L0)，结合题图甲中数据得L0＝‎3.0 cm，k＝200 N/m.‎ ‎(2)由题图乙知指针所示刻度为‎1.50 cm，由F＝k(L0－L)，可求得此时弹力为F＝3 N，故所挂钩码的个数为3个．‎ ‎5．某物理小组想要探究弹力和弹簧伸长的关系，并测量弹簧的劲度系数．做法是先将弹簧的一端固定在铁架台上，然后将最小刻度是毫米的刻度尺竖直放在弹簧的一侧，并使弹簧另一端的指针恰好落在刻度尺上．当弹簧自然下垂时，将指针指示的刻度值记作L0；弹簧下端挂一个‎50 g的砝码时，指针指示的刻度值记作L1；弹簧下端挂两个‎50 g的砝码时，指针指示的刻度值记作L2；…；挂七个‎50 g的砝码时，指针指示的刻度值记作L7.测量记录如下表：‎ 代表符号 L0‎ L1‎ L2‎ L3‎ L4‎ L5‎ L6‎ L7‎ 刻度值/cm ‎1.70‎ ‎3.40‎ ‎5.10‎ ‎8.60‎ ‎10.30‎ ‎12.10‎ ‎(1)实验中，L3和L7两个值还没有记录，请你根据如图所示的指针位置将这两个测量值依次写出6.85,14.05；‎ ‎(2)为了充分利用测量数据，该同学将所测得的数值按如下方法逐一求差．分别计算出三个差值：d1＝L4－L0＝‎6.90 cm，d2＝L5－L1＝‎6.90 cm，d3＝L6－L2＝‎7.00 cm，请你给出第4个差值d4＝L7－L3＝‎7.20 cm；‎ ‎(3)根据以上差值，可以计算出每增加‎50 g砝码的弹簧平均伸长量ΔL，则ΔL＝；(用d1、d2、d3、d4表示)‎ ‎(4)计算弹簧的劲度系数k＝28 N/m.(g取‎9.8 m/s2)‎ 解析：(1)刻度尺的最小分度值为‎1 mm，所以L3＝‎6.85 cm，L7＝‎14.05 cm；(2)根据题意：d4＝L7－L3＝‎14.05 cm－‎6.85 cm＝‎7.20 cm；(3)因为d1＝L4－L0＝4ΔL，d2＝L5－L1＝4ΔL，d3＝L6－L2＝4ΔL，d4＝L7－L3＝4ΔL，所以：ΔL＝；(4)充分利用测量数据得 k＝＝ N/m＝28 N/m.‎ ‎6．把两根轻质弹簧串联起来测量它们各自的劲度系数，如图甲所示．‎ ‎(1)未挂钩码之前，指针B指在刻度尺如图乙所示的位置上，其示数为‎11.50 cm；‎ ‎(2)将质量‎50 g的钩码逐个挂在弹簧Ⅰ的下端，逐次记录两弹簧各自的伸长量；所挂钩码的质量m与每根弹簧的伸长量x可描绘出如图丙所示的图象，由图象可计算出弹簧Ⅱ的劲度系数kⅡ＝28 N/m；(取重力加速度g＝‎9.8 m/s2)‎ ‎(3)图丙中，当弹簧Ⅰ的伸长量超过‎17 cm时其图线为曲线，由此可知，挂上第5个钩码时，拉力已经超过它的弹性限度，这对测量弹簧Ⅱ的劲度系数没有 ‎(填“有”或“没有”)影响(弹簧Ⅱ的弹性限度足够大)．‎ 解析：(1)毫米刻度尺读数需估读到最小分度的下一位，指针B示数为‎11.50 cm.(2)由题图丙中的数据可知，弹簧Ⅱ的形变量为Δx＝‎7.00 cm时，拉力F＝mg＝4×0.05×9.8 N＝1.96 N，根据胡克定律可知kⅡ＝＝＝28 N/m.(3)由题图丙中的数据可知，当弹簧Ⅰ的伸长量为‎14 cm时，对应的拉力F′是1.96 N，所以其劲度系数k1＝＝＝14 N/m；弹簧Ⅰ的伸长量为‎17 cm时，对应的拉力F″＝k1Δx″＝14×0.17 N＝2.38 N，n＝≈4.86.由此可知，挂上第5个钩码时，拉力已经超过弹簧Ⅰ的弹性限度，这时弹簧Ⅱ的图线仍然是直线，说明对测量弹簧Ⅱ的劲度系数没有影响．‎ ‎7．将两根自然长度相同、劲度系数不同、粗细也不同的弹簧套在一起，看成一根新弹簧，设原粗弹簧(记为A)劲度系数为k1，原细弹簧(记为B)劲度系数为k2，套成的新弹簧(记为C)劲度系数为k3.关于k1、k2、k3的大小关系，同学们做出了如下猜想：‎ 甲同学：和电阻并联相似，可能是＝＋ 乙同学：和电阻串联相似，可能是k3＝k1＋k2‎ 丙同学：可能是k3＝ ‎(1)为了验证猜想，同学们设计了相应的实验(装置见图甲)．‎ ‎(2)简要实验步骤如下，请完成相应填空．‎ ‎①将弹簧A悬挂在铁架台上，用刻度尺测量弹簧A的自然长度L0；‎ ‎②在弹簧A的下端挂上钩码，记下钩码的个数n、每个钩码的质量m和当地的重力加速度大小g，并用刻度尺测量弹簧的长度L1；‎ ‎③由F＝nmg计算弹簧的弹力，由x＝L1－L0计算弹簧的伸长量，由k＝计算弹簧的劲度系数；‎ ‎④改变钩码的个数，重复实验步骤②、③，并求出弹簧A的劲度系数的平均值k1；‎ ‎⑤仅将弹簧分别换为B、C，重复上述操作步骤，求出弹簧B、C的劲度系数的平均值k2、k3.比较k1、k2、k3并得出结论．‎ ‎(3)图乙是实验得到的图线，由此可以判断乙同学的猜想正确．‎ 解析：(2)由步骤②知，弹簧的弹力等于钩码的总重力，即F＝nmg，由步骤③知，可以建立F与x的关系式，要想多得几组数据，就需改变钩码的个数．(3)题图乙得到的实验图线的斜率为弹簧的劲度系数，由图中数据得k3＝k2＋k1，所以乙同学的猜想正确．‎ ‎8.某同学用图甲所示的装置测量木块与木板之间的动摩擦因数．跨过光滑定滑轮的细线两端分别与木块和弹簧秤相连，滑轮和木块间的细线保持水平，在木块上方放置砝码．缓慢向左拉动水平放置的木板，当木块和砝码相对桌面静止且木板仍在继续滑动时，弹簧秤的示数即为木块受到的滑动摩擦力的大小．某次实验所得数据在下表中给出，其中f4的值可从图乙中弹簧秤的示数读出.‎ 砝码的质量m/kg ‎0.05‎ ‎0.10‎ ‎0.15‎ ‎0.20‎ ‎0.25‎ 滑动摩擦力f/N ‎2.15‎ ‎2.36‎ ‎2.55‎ f4‎ ‎2.93‎ 回答下列问题：‎ ‎(1)f4＝2.75 N；‎ ‎(2)在图丙的坐标纸上补齐未画出的数据点并绘出fm图线；‎ 答案：如图所示 ‎(3)f与m、木块质量M、木板与木块之间的动摩擦因数μ及重力加速度大小g之间的关系式为f＝μ(M＋m)g，fm图线(直线)的斜率的表达式为k＝μg；‎ ‎(4)取g＝‎9.80 m/s2，由绘出的fm图线求得μ＝0.40.(保留两位有效数字)‎ 解析：(1)弹簧秤读数时应估读，弹簧秤示数为2.75 N.‎ ‎(2)按数据描点连线如图所示．‎ ‎(3)由于砝码和木块相对桌面静止，由平衡条件可知f＝μ(M＋m)g，则有f＝μMg＋μmg，fm图象中k＝μg.‎ ‎(4)由k＝μg可得μ＝＝≈0.40.‎