【物理】2019届一轮复习人教版圆周运动中的临界问题学案

【物理】2019届一轮复习人教版圆周运动中的临界问题学案

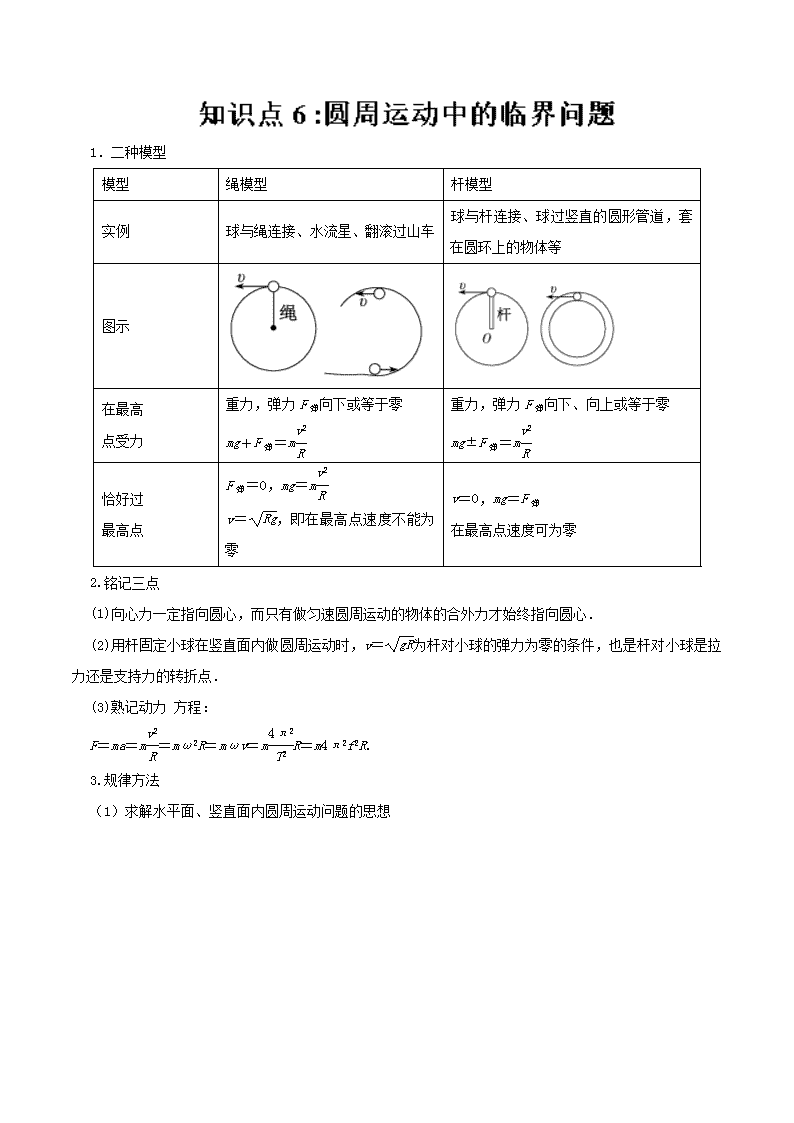
‎1．二种模型 育 出^ 版 ]‎ 模型 绳模型 杆模型 实例 球与绳连接、水流星、翻滚过山车 球与杆连接、球过竖直的圆形管道，套在圆环上的物体等 图示 在最高 点受力 重力，弹力F弹向下或等于零 mg＋F弹＝m 重力，弹力F弹向下、向上或等于零 mg±F弹＝m 恰好过 最高点 F弹＝0，mg＝m v＝，即在最高点速度不能为零 v＝0，mg＝F弹 在最高点速度可为零 ‎2.铭记三点 ‎(1)向心力一定指向圆心，而只有做匀速圆周运动的物体的合外力才始终指向圆心．‎ ‎(2)用杆固定小球在竖直面内做圆周运动时，v＝为杆对小球的弹力为零的条件，也是杆对小球是拉力还是支持力的转折点．‎ ‎(3)熟记动力 方程：‎ F＝ma＝m＝mω2R＝mωv＝mR＝m4π2f2R.‎ ‎3.规律方法[w w w. ste ^p ]‎ ‎（1）求解水平面、竖直面内圆周运动问题的思想 ‎ ‎（2）．系在绳上的物体在竖直平面内做圆周运动的条件是v高≥；[ ^: s tep ]‎ 绳改为杆后，则v最高≥0均可；‎ 在最高点的速度v最高＞时，杆拉物体；‎ v最高＜时杆支持物体；‎ v最高＝时杆的作用力为零．‎ ‎（3）．物体随圆盘一起做圆周运动的最大角速度为ω＝，与物体的质量无关，决定于物体到圆心的距离R和动摩擦因数μ.‎ ‎（4）．火车转弯时既不挤压内轨，也不挤压外轨时的行驶速率约为v限＝，取决于内、外轨的高度差h、内外轨间距L及铁路弯道的轨道半径r.[来 源 : step.co m ]‎ 典例分析：‎ ‎【例1】　(多选)如图，两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上，a与转轴OO′的距离为l，b与转轴的距离为2l.木块与圆盘的最大静摩擦力为木块所受重力的k倍，重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动，用ω表示圆盘转动的角速度，下列说法正确的是(　　)‎ A．b一定比a先开始滑动[中 国 教^育出版 ]‎ B．a、b所受的摩擦力始终相等[来^源: 中教 ]‎ C．ω＝ 是b开始滑动的临界角速度 D．当ω＝ 时，a所受摩擦力的大小为kmg ‎【答案】　AC ‎【例2】　如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω转动，盘面上离转轴距离2.5 m处有一小物体与圆盘始终保持相对静止．物体与盘面间的动摩擦因数为(设最大静摩擦力等于滑动摩擦力)，盘面与水平面的夹角为30°，g取10 m/s2.则ω的最大值是(　　)‎ A. rad/s B. rad/s C．1.0 rad/s D．0.5 rad/s ‎【答案】　C ‎【解析】　在圆周运动的最低点达到临界状态，受力分析，应用正交分解法，列出方程：μmgcos30°－mgsin30°＝mω2r，把μ＝、r＝2.5 m，代入解得临界ω＝1.0 rad/s.‎ ‎【例3】　如图所示，一质量为m＝0.5 kg的小球，用长为L＝0.4 m的轻绳拴住在竖直平面内做圆周运动．求 ‎[中国^教 育出 版 ]‎ ‎(1)小球要做完整的圆周运动，在最高点的速度至少为多大？[www. ^ st ep ]‎ ‎(2)当小球在最高点的速度为4 m/s时，细线拉力多大？‎ ‎(3)若轻绳能承受的最大张力为45 N，求小球的速度不能超过多大值？[来^源: 中教 ]‎ ‎【答案】v≥2 m/s； F2＝15 N. ； 4 m/s.‎ ‎【解析】　[来 源: 中 国教育出 版 ]‎ ‎[中 国教 育^出版 ]‎ ‎(2)将v2＝4 m/s代入①得F2＝15 N.‎ ‎(3)由分析可知小球在最低点张力最大，对小球受力分析如图3－3－5，由牛顿第二定律得 F3－mg＝[来 源: s tep. co m^]‎ 将F3＝45 N代入③得v3＝4 m/s，[来 源:中教 ^ ]‎ 即小球的速度不能超过4 m/s.‎ 专题练习 ‎1 .(2017年湖北武汉模拟)如图所示的装置可以测量子弹的飞行速度．在一根轴上相距s＝1 m处安装两个平行的薄圆盘，使轴带动两圆盘以n＝3 000 r/min的转速匀速转动，飞行的子弹平行于轴沿一条直线穿过两圆盘，即在盘上留下两个小孔，现测得两小孔所在半径间的夹角为30°，子弹飞行的速度大小可能是下述的(设在穿过两圆盘的过程中子弹的速度保持不变)(　　)‎ A．500 m/s B．600 m/s C．700 m/s D．800 m/s ‎【答案】：B ‎2．(多选)如图所示，半径r＝0.5 m的光滑圆轨道被竖直固定在水平地面上，圆轨道最低处有一小球(小球的半径比r小很多)．现给小球一个水平向右的初速度v0，要使小球不脱离轨道运动，重力加速度大小g取10 m/s2，v0应满足(　　)‎ ‎[ : s t ep.c om]‎ A．v0≥0 B．v0≥2 m/s C．v0≥5 m/s D．v0≤ m/s ‎【答案】：CD ‎【解析】：最高点的临界情况为mg＝m，解得v＝，小球从最低点到最高点的过程，根据动能定理得，－mg·2r＝mv2－mv，解得v0＝5 m/s.若恰好不通过圆心高度，根据动能定理有－mgr＝0－mv，解得v0＝＝ m/s，所以v0应满足的条件是v0≥5 m/s或v0≤ m/s，故C、D正确，A、B错误．‎ ‎3．如图所示，用一根细绳一端系一个小球，另一端固定，给小球不同的初速度，使小球在水平面内做角速度不同的圆周运动，则下列细绳拉力F、悬点到轨迹圆圆心高度h、向心加速度a、线速度v与角速度平方ω2的关系图象正确的是(　　)‎ ‎ step .^com]‎ ‎【答案】：A ‎4．(2017年河北保定质检)如图所示，内壁光滑的竖直圆桶，绕中心轴做匀速圆周运动，一物块用细绳系着，绳的另一端系于圆桶上表面圆心，且物块贴着圆桶内表面随圆桶一起转动，则(　　)‎ ‎[来^源 :中 教 ]‎ A．绳的张力可能为零 B．桶对物块的弹力不可能为零 C．随着转动的角速度增大，绳的张力保持不变 D．随着转动的角速度增大，绳的张力一定增大 ‎【答案】C ‎【解析】当物块随圆桶做圆周运动时，绳的拉力的竖直分力与物块的重力保持平衡，因此绳的张力为一定值，且不可能为零，A、D项错误，C项正确；当绳的水平分力提供向心力的时候，桶对物块的弹力恰好为零，B项错误． 中 国教育 出 版 ]‎ ‎5．(2017年河南八市重点高中质量监测)如图所示，一质量为M 的光滑大圆环，用一细轻杆固定在竖直平面内；套在大环上质量为m的小环(可视为质点)处于静止状态，现轻微扰动一下，小环从大环的最高处由静止滑下．重力加速度大小为g，当小环滑到大环的最低点时，下列说法正确的是(　　)‎ ‎[中国教育 ^出版 ]‎ A．大环对小环的弹力为3mg B．大环对小环的弹力为4mg C．轻杆对大环的弹力为Mg＋5mg D．轻杆对大环的弹力为Mg＋6mg ‎【答案】：C ‎6．(多选)(2017年开封高三5月冲剌)如图所示，在匀速转动的水平盘上，沿半径方向放着用细线相连的质量相等的两个物体A和B，它们分居圆心两侧，与圆心距离分别为RA＝r，RB＝2r，与盘间的动摩擦因数μ相同，当圆盘转速加快到两物体刚好还未发生滑动时，最大静摩擦力等于滑动摩擦力，下列说法正确的是 (　　)‎ A．此时绳子张力为T＝3μmg B．此时圆盘的角速度为ω＝ C．此时A所受摩擦力方向沿半径指向圆外 D．此时烧断绳子，A仍相对盘静止，B将做离心运动 ‎【答案】：ABC[w ww. s t ep ]‎ ‎7．(多选)如图所示，一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处，B为轨道最高点，C、D为圆的水平直径两端点．轻质弹簧的一端固定在圆心O点，另一端与小球拴接，已知弹簧的劲度系数为k＝，原长为L＝2R，弹簧始终处于弹性限度内，若给小球一水平初速度v0，已知重力加速度为g，则(　　)[来^源:中国教育出 版 ]‎ A．无论v0多大，小球均不会离开圆轨道 B．若，小球就能做完整的圆周运动 D．只要小球能做完整圆周运动，则小球与轨道间最大压力与最小压力之差与v0无关 中国 ^ 教 育 出版 ]‎ ‎【答案】：ACD ‎【解析】：A、B项，由题中条件易知弹簧的弹力始终为Fk＝kR＝mg，方向背离圆心，易得在最高点以外的任何地方轨道对小球均会有弹力作用，所以无论初速度多大，小球均不会脱离轨道，故A正确，B错．C项，易知，小球在运动过程中只有重力做功，机械能守恒，小球做完整圆周运动的临界情况是最高点时速度为零，此情况下，有mv＝2mgR，解得v0＝，所以只要v0>，小球就能做完整的圆周运动，故C正确．D项，小球做完整的圆周运动时，最高点时小球与轨道间压力最小，设为F1，最低点时对轨道压力最大，设为F2，设最高点时速度为v.易得v＝，则有F2＝mg＋kR＋＝2mg＋，F1＝＝－4mg，F2－F1＝6mg，所以只要小球能做完整圆周运动，则小球与轨道间的最大压力与最小压力之差与初速度无关，故D正确．‎ ‎8.(多选)如图所示，在水平转台上放一个质量M＝2.0 kg的木块，它与台面间的最大静摩擦力Ffm＝6.0 N，绳的一端系住木块，另一端穿过转台的中心孔O(为光滑的)悬吊一质量m＝1.0 kg的小球，‎ 当转台以ω＝5.0 rad/s的角速度转动时，欲使木块相对转台静止，则它到O孔的距离不可能是 ‎[来 源: 中教 ]‎ A．6 cm B．15 cm[ww^w . step .co m]‎ C．30 cm D．34 cm ‎【答案】　AD[ : step.c om]‎ ‎【解析】M在水平面内转动时，平台对M的支持力与Mg相平衡，拉力与平台对M的静摩擦力的合力提供向心力．‎ 设M到转台中心的距离为R，M以角速度ω转动所需向心力为Mω2R，‎ 若Mω2R＝T＝mg，此时平台对M的摩擦力为零．‎ 若R1＞R，Mω2R1＞mg，平台对M的摩擦力方向向左，由牛顿第二定律：‎ f＋mg＝Mω2R1，‎ ‎9．(2017·焦作二模)如图所示，ABC为竖直平面内的金属半圆环，AC连线水平，AB为固定在A、B两点间的直金属棒，在直棒和圆环的BC部分上分别套着小环M、N(棒和半圆环均光滑)，现让半圆环绕竖直对称轴以角速度1做匀速转动，小环M、N在图示位置．如果半圆环的角速度变为2，2比1稍微小一些．关于小环M、N的位置变化，下列说法正确的是(　　)‎ A．小环M将到达B点，小环N将向B点靠近稍许 B．小环M将到达B点，小环N的位置保持不变 C．小环M将向B点靠近稍许，小环N将向B点靠近稍许 D．小环M向B点靠近稍许，小环N的位置保持不变 ‎【答案】　A ‎10．(多选)如图所示，叠放在水平转台上的物体A、B、C能随转台一起以角速度ω匀速转动，A、B、C的质量分别为3m、2m、m，A与B、B和C与转台间的动摩擦因数均为μ，A和B、C离转台中心的距离分别为r、1.5r.设本题中的最大静摩擦力等于滑动摩擦力．以下说法中正确的是(　　) 中教 ^ ]‎ ‎ 中 教 ^]‎ A．B对A的摩擦力一定为3μmg ‎ B．B对A的摩擦力一定为3mω2r C．转台的角速度一定满足ω≤ ‎ D．转台的角速度一定满足ω≤ ‎【答案　】BC ‎【解析】要使A能够与B一起以角速度ω转动，根据牛顿第二定律可知，B对A的摩擦力一定等于A物体所需向心力的值，即Ff＝3mω2r，B项正确．要使A、B两物体同时能随转台一起以角速度ω匀速转动，则对于A，有3μmg≥3mrω2，对AB，有5μmg≥5mrω2，对于C，有μmg≥mrω2，综合以上，可得ω≤ ，C项正确．‎ ‎11.(多选)如图所示，将长为3L的轻杆穿过光滑水平转轴O，两端分别固定质量为2m的球A和质量为3m的球B，A到O的距离为L，现使杆在竖直平面内转动，当球B运动到最高点时，球B恰好对杆无作用力，两球均视为质点．则球B在最高点时(　　)[中国 教 ^育 出版 ]‎ ‎ 中 国教育出 版 ]‎ A．球B的速度大小为 B．球A的速度大小为 C．球A对杆的作用力大小为3mg D．水平转轴对杆的作用力为5mg ‎【答案】　BC[来 源:中教^ ]‎ ‎[中 国 ^教育出 版 ]‎ ‎12.(2017·西安市模拟)如图所示，一个质量为M的人，站在台秤上，一长为R的悬线一端系一个质量为m的小球，手拿悬线另一端，小球绕悬线另一端点在竖直平面内做圆周运动，且小球恰好能通过圆轨道最高点，则下列说法正确的是(　　)‎ ‎[中^国教 育 出版 ]‎ A．小球运动到最低点时，台秤的示数最大且为(M＋6m)g 中 国 教育 出版 ]‎ B．小球运动到最高点时，台秤的示数最小且为Mg C．小球在a、b两个位置时，台秤的示数不相同[w ww . step . com]‎ D．小球从最高点运动到最低点的过程中台秤的示数增大，人处于超重状态 ‎【答案】　A[ ^: step.co m ]‎ ‎【解析】小球恰好能通过圆轨道最高点，在最高点，细线中拉力为零，小球速度vb＝.小球从最高点运动到最低点，由机械能守恒定律，mvb2＋mg×2R＝mvd2，在最低点，由牛顿第二定律，F－mg＝m，联立解得细线中拉力F＝6mg.小球运动到最低点时，台秤的示数最大且为Mg＋F＝(M＋6m)g，A项正确；‎ ‎[中 国 教 育出^版 ]‎ ‎13．(2017·定州市模拟)如图所示，圆筒的内壁光滑，一端B固定在竖直转轴OO′上，圆筒可随轴转动，它与水平面的夹角始终为30°，在筒内有一个用轻质弹簧连接的小球A(小球直径略小于圆筒内径)，A的质量为m，弹簧的另一端固定在圆筒的B端，弹簧原长为L，当圆筒静止时A、B之间的距离为L(L远大于小球直径)．现让圆筒开始转动，其角速度从0开始缓慢增大，当角速度增大到某一值时保持匀速转动，此时小球A、B之间的距离为2L，重力加速度大小为g，求圆筒保持匀速转动时的角速度ω0.‎ ‎【答案】　 ‎【解析　】当圆筒静止时A、B之间的距离为L，可知弹簧的形变量Δx＝，‎ 根据平衡有mgsin30°＝k·.‎ 当圆筒转动，AB间距离为2L时，受力如图，‎ ‎[中^ 国教育出版 ]‎ 在竖直方向上，有Ncos30°＝ksin30°＋mg，‎ 水平方向上，有kcos30°＋Nsin30°＝m·2Lsin60°ω02，‎ 联立解得ω0＝.‎ ‎14.如图所示，光滑圆杆MN段竖直，OC段水平且与MN相接于O点，两杆分别套有质量为m的环A和2m的环B，两环的内径比杆的直径稍大，A、B用长为2L的轻绳连接，A、O用长为L的轻绳连接，现让装置绕竖直杆MN做匀速圆周运动，当ω＝时，OA段绳刚好要断，AB段绳能承受的拉力足够大，求：‎ ‎(1)OA段绳刚刚拉直时转动的角速度多大；‎ ‎(2)OA段绳能承受的最大的拉力；‎ ‎(3)当ω＝2且转动稳定时，A向外侧移动的距离多大．‎ ‎【答案】　(1)　(2)mg　(3) L ‎(2)根据牛顿第二定律得，‎ Tm＋TABsinθ＝mLω2，‎ 解得Tm＝mg，‎ ‎15．如图所示，水平传送带的右端与竖直面内的用光滑钢管弯成的“9”形固定轨道相接，钢管内径很小．传送带的运行速度为v0＝6 m/s，将质量m＝1 kg的可看作质点的滑块无初速地放到传送带A端，传送带长度为L＝12 m，“9”字全高H＝0.8 m，“9”字CDE部分圆弧半径为R＝0.2 m的圆弧，滑块与传送带间的动摩擦因数为μ＝0.3，取重力加速度g＝10 m/s2.‎ ‎(1)求滑块从传送带A端运动到B端所需要的时间；‎ ‎(2)求滑块滑到轨道最高点D时对轨道作用力的大小和方向；‎ ‎(3)若滑块从“9”形轨道F点水平抛出后，恰好垂直撞在倾角θ＝45°的斜面上的P点，求P、F两点间的竖直高度h.‎ ‎【答案】（1）t＝3 s； （2）FN＝90 N，方向竖直向下 （3）h＝1.4 m[来 源: 中教 ^ ]‎ ‎【解析】(1)滑块在传送带上加速运动时，‎ 由牛顿第二定律有μmg＝ma 解得a＝μg＝3 m/s2‎ 加速到与传送带共速的时间t1＝＝2 s ‎2 s内滑块的位移x1＝at＝6 m 之后滑块做匀速运动的位移x2＝L－x1＝6m 所用时间t2＝＝1 s 故t＝t1＋t2＝3 s[中^国教育 出 版 ]‎ ‎(3)滑块由B运动到F的过程中由动能定理得：‎ ‎－mg(H－2R)＝mv－mv 滑块撞击P点时，其速度沿竖直方向的分速度为：‎ vy＝ 竖直方向有：v＝2gh[来 源:中^国 教育出 版 ]‎ 解得：h＝1.4 m ‎16.如图所示，一块足够大的光滑平板放置在水平面上，能绕水平固定轴MN调节其与水平面所成的倾角．板上一根长为l＝0.60 m的轻细绳，它的一端系住一质量为m的小球P，另一端固定在板上的O点．当平板的倾角固定为α时，先将轻绳平行于水平轴MN拉直，然后给小球一沿着平板并与轻绳垂直的初速度v0＝3.0 m/s.若小球能保持在板面内做圆周运动，倾角α的值应在什么范围内？(取重力加速度g＝10 m/s2)‎ ‎【答案】0°≤α≤30°‎ ‎【解析】小球在倾斜平板上运动时受到绳子拉力、平板弹力、重力．在垂直平板方向上合力为0，重力在沿平板方向的分量为mgsinα 小球在最高点时，由绳子的拉力和重力沿平板方向的 分力的合力提供向心力，有T＋mgsinα＝①‎ 研究小球从释放到最高点的过程，根据动能定理有 T＝0时，联立①②解得sin α＝，解得α＝30°‎ 故α的范围为0°≤α≤30°. ‎ ‎[ :中^教 ]‎