2018届二轮复习　物体的曲线运动课件（共49张）（全国通用）

2018届二轮复习　物体的曲线运动课件（共49张）（全国通用）

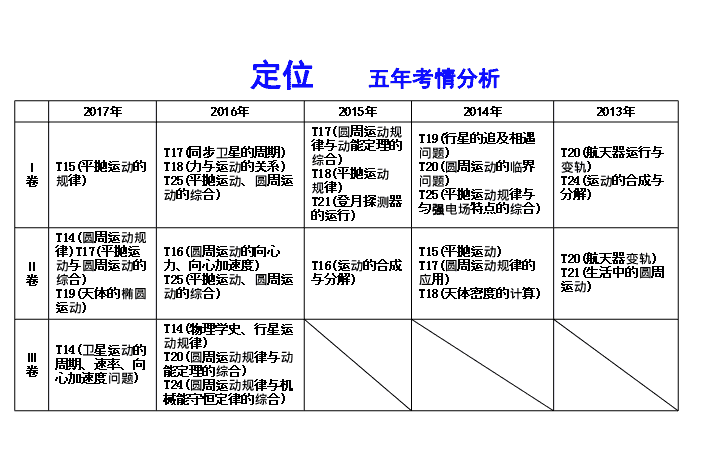
专题三　力与曲线运动 定位 五年考情分析 2017 年 2016 年 2015 年 2014 年 2013 年 Ⅰ 卷 T15( 平抛运动的规律 ) T17( 同步卫星的周期 ) T18( 力与运动的关系 ) T25( 平抛运动、圆周运动的综合 ) T17( 圆周运动规律与动能定理的综合 ) T18( 平抛运动 规律 ) T21( 登月探测器的运行 ) T19( 行星的追及相遇问题 ) T20( 圆周运动的临界问题 ) T25( 平抛运动规律与匀强电场特点的综合 ) T20( 航天器运行与变轨 ) T24( 运动的合成与分解 ) Ⅱ 卷 T14( 圆周运动规律 )T17( 平抛运动与圆周运动的综合 ) T19( 天体的椭圆运动 ) T16( 圆周运动的向心 力、向心加速度 ) T25( 平抛运动、圆周运动的综合 ) T16( 运动的合成与分解 ) T15( 平抛运动 ) T17( 圆周运动规律的应用 ) T18( 天体密度的计算 ) T20( 航天器变轨 ) T21( 生活中的圆周运动 ) Ⅲ 卷 T14( 卫星运动的周期、速率、向心加速度问题 ) T14( 物理学史、行星运动规律 ) T20( 圆周运动规律与动能定理的综合 ) T24( 圆周运动规律与机械能守恒定律的综合 ) 专题 定位 本专题解决的是曲线运动规律及其与牛顿运动定律的综合问题 . 高考对本专题的考查频率极高 , 力与天体运动部分以选择题为主 , 难度适中 ; 力与曲线运动部分 , 既有选择题 , 也有计算题 , 难度中上 . 分解思想、合成法、正交分解法、临界值的思想是用到的主要思想方法 ; 抛体运动、圆周运动、直线运动组合问题及功能综合问题等是考查的重点 . 应考 建议 1. 熟练掌握平抛和匀速圆周运动的运动学公式及适用条件 . 2. 运用运动的合成和分解、动力学规律和功能关系解决直线运动、圆周运动、平抛运动的组合性问题 , 分析衔接点的速度是解决问题的关键 . 3. 运用两个模型、两条思路是解决天体运动与航天问题的基础 , 重点关注我国航天工程的最新成就 . 第 1 讲　物体的曲线运动 整 合 突 破 实 战 整合 网络要点重温 【 网络构建 】 【 要点重温 】 1.物体做曲线运动的条件:当物体所受合外力的方向跟它的速度方向 时,物体做曲线运动. 2.运动的合成与分解的运算法则: 定则. 3.做平抛运动的物体,平抛运动的时间完全由 决定,t= . 4.平抛(或类平抛)运动的推论 ①任意时刻速度的反向延长线一定通过此时水平位移的 . 不在同 一条直线上 平行四边形 高度 中点 5. 水平面内圆周运动临界问题 (1) 水平面内做圆周运动的物体其向心力可能由弹力、摩擦力等力提供 , 常涉及绳的张紧与松弛、接触面分离等临界状态 . (2) 常见临界条件 : 绳子松弛的临界条件是绳的张力 F T = ; 接触面滑动的临界条件是拉力 F=F fmax ; 接触面分离的临界条件是接触面间的弹力 F N = . 6. 竖直平面内圆周运动的两种临界问题 (1) 绳模型 : 半径为 R 的圆形轨道 , 物体能通过最高点的条件是 v≥ . (2) 杆模型 : 物体能通过最高点的条件是 v> . 0 0 0 突破 热点考向聚焦 热点考向一　运动的合成与分解 【 核心提炼 】 1. 运动合成与分解的一般思路 (1) 明确合运动或分运动的运动性质 . (2) 明确是在哪两个方向上的合成或分解 . (3) 找出各个方向上已知的物理量 ( 速度、位移、加速度 ). (4) 运用力与速度的关系或矢量的运算法则进行分析求解 . 2. 分析运动的合成与分解问题 , 要注意运动的分解方向 , 一般情况按实际运动效果进行分解 . 绳关联的情景中 , 物体的实际运动为合运动 , 相应的速度为合速度 ; 实际运动有两个运动效果 , 一是使绳子伸长 , 二是使绳子转动 . 3. 小船过河的时间 t= , 其中 v 垂 为小船在静水中的速度沿垂直于河岸方向的分速度 . 【 典例 1】 ( 2017 · 河南平顶山模拟 ) 如图所示 , 在竖直平面的 xOy 坐标系中 ,Oy 竖直向上 ,Ox 水平 . 设平面内存在沿 x 轴正方向的恒定风力 . 一小球从坐标原点沿 Oy 方向竖直向上抛出 , 初速度为 v 0 =4 m/s, 不计空气阻力 , 到达最高点的位置如图中 M 点所示 .( 坐标格为正方形 ,g 取 10 m/s 2 ) 求 : (1) 小球在 M 点的速度 v 1 的大小 ; 答案 : (1)6 m/s 　 (2) 在图中定性画出小球的运动轨迹并标出小球落回 x 轴时的位置 N; 解析 : (2) 由竖直方向的对称性可知 , 小球再经过 t 1 到 x 轴 , 水平方向做初速度为零的匀加速直线运动 , 在 2t 1 时间内的平均速度为 v 1 , 所以回到 x 轴时落到 x=v 1 ×2t 1 =12s 0 处 , 位置 N 的坐标为 (12,0). 答案 : (2) 见解析图 (3) 小球到达 N 点的速度 v 2 的大小 . 【 拓展延伸 】 在 “ 典例 1 ” 中 , 若将恒定风力改为电场力 , 且带电小球斜着进入电场 . 电场为沿 x 轴正方向、电场强度为 E 的有界匀强电场 , 若质量为 m, 电荷量为 q 的带正电小球从 O 点以初速度 v 0 沿与 x 轴负方向成 θ 角进入电场 , 如图所示 , 小球离开电场时的速度方向竖直向下 . 求 : (1) 小球在电场中运动的时间 ; 答案 : 见解析 (2) 出电场时沿水平方向及竖直方向位移大小 . 答案 : 见解析 【 预测练习 1】 ( 2017 · 河北石家庄质检 ) 小船过河时 , 船头与上游河岸夹角为 α, 其航线恰好垂直于河岸 , 已知船在静水中的速度为 v, 现水流速度稍有增大 , 为保持航线不变 , 且能准时到达河对岸 , 下列措施中可行的是 ( 　 　 ) A. 减小 α 角 , 减小船速 v B. 减小 α 角 , 增大船速 v C. 增大 α 角 , 增大船速 v D. 增大 α 角 , 减小船速 v 解析 : 由题意可知 , 船在静水中的速度为 v, 其航线恰好垂直于河岸 , 当水流速度 v 水 稍有增大 , 变成 v 水 ′, 为保持航线不变 , 且准时到达对岸 , 即 v 合 大小方向都不变 , 那么船速由 v 变成 v′, 如图所示 , 可得 α 减小 ,v 变大 , 选项 B 正确 . B 热点考向二　抛体运动问题　　　　　　　 　　　　　　 　　　　　　 【 核心提炼 】 1.求解平抛(类平抛)运动的技巧 (1)求解落点问题时,一般建立坐标系,由两个方向遵循的规律列出位移方程,由此确定其落点. (2)求解末速度的大小和方向问题时,一般要建立水平分速度和竖直分速度之间的关系,由此确定其末速度. (3)如图所示,分解某一过程的位移和某一位置瞬时速度,则可以获得两个直角三角形.一般该类运动问题都可以在这两个直角三角形中解决. 2. 平抛运动与斜面相关的两个结论 (2) 若平抛的物体垂直打在斜面上 , 则物体打在斜面上瞬间 , 其水平速度与竖直速度之比等于斜面倾角的正切值 . BC 〚审题突破〛 【 预测练习 2】 ( 2017 · 山东烟台模拟 ) ( 多选 ) “ 套圈 ” 是一项老少皆宜的体育运动项目 . 如图所示 , 水平地面上固定着 3 根直杆 1,2,3, 直杆的粗细不计 , 高度均为 0.1 m, 相邻两直杆之间的距离为 0.3 m. 比赛时 , 运动员将内圆直径为 0.2 m 的环沿水平方向抛出 , 刚抛出时环平面距地面的高度为 1.35 m, 环的中心与直杆 1 的水平距离为 1 m. 假设直杆与环的中心位于同一竖直面 , 且运动中环心始终在该平面上 , 环面在空中保持水平 , 忽略空气阻力的影响 ,g 取 10 m/s 2 . 以下说法正确的是 ( 　 　 ) A. 如果能够套中直杆 , 环抛出时的水平初速度不能小于 1.8 m/s B. 如果能够套中第 2 根直杆 , 环抛出时的水平初速度在 2.4 m/s 到 2.8 m/s 之间 C. 如以 2.3 m/s 的水平初速度将环抛出 , 就可以套中第 1 根直杆 D. 如环抛出的水平速度大于 3.3 m/s, 就不能套中第 3 根直杆 AB 热点考向三　圆周运动问题 【 核心提炼 】 1. 解决圆周运动问题的关键 (1) 要进行受力分析 , 明确向心力的来源 , 确定圆心以及半径 . 2. 对于竖直平面内的圆周运动要注意区分 “ 轻绳模型 ” 和 “ 轻杆模型 ” , 明确两种模型过最高点时的临界条件 . 3. 解决竖直平面内的圆周运动的基本思路是 “ 两点一过程 ” (1) “ 两点 ” 即最高点和最低点 , 在最高点和最低点对物体进行受力分析 , 确定向心力 , 根据牛顿第二定律列方程 . (2) “ 一过程 ” 即从最高点到最低点 , 往往由动能定理将这两点的速度联系起来 . 【 典例 3】 ( 多选 ) 如图所示 , 粗糙水平圆盘上 , 质量相等的 A,B 两物块叠放在一起 , 随圆盘一起做匀速圆周运动 , 则下列说法正确的是 ( 　 　 ) A.B 的向心力是 A 的向心力的 2 倍 B. 盘对 B 的摩擦力是 B 对 A 的摩擦力的 2 倍 C.A,B 都有沿半径向外滑动的趋势 D. 若 B 先滑动 , 则 B 对 A 的动摩擦因数 μ A 小于盘对 B 的动摩擦因数 μ B BC BC 热点考向四　平抛与圆周运动组合问题　　　　　　　 　　　　　　 　　　　　　 【 核心提炼 】 平抛运动与圆周运动的组合题 , 关键是找到两者的速度关系 . 若先做圆周运动后做平抛运动 , 则圆周运动的末速度等于平抛运动的水平初速度 ; 若物体平抛后进入圆轨道 , 圆周运动的初速度等于平抛末速度在圆切线方向的分速度 . 【典例4】 ( 2016 · 全国Ⅱ卷,25 ) 轻质弹簧原长为2l,将弹簧竖直放置在地面上,在其顶端将一质量为5m的物体由静止释放,当弹簧被压缩到最短时,弹簧长度为l.现将该弹簧水平放置,一端固定在A点,另一端与物块P接触但不连接.AB是长度为5l的水平轨道,B端与半径为l的光滑半圆轨道BCD相切,半圆的直径BD竖直,如图所示.物块P与AB间的动摩擦因数μ=0.5.用外力推动物块P,将弹簧压缩至长度l,然后放开,P开始沿轨道运动.重力加速度大小为g. (1) 若 P 的质量为 m, 求 P 到达 B 点时速度的大小以及它离开圆轨道后落回到 AB 上的位置与 B 点之间的距离 . (2) 若 P 能滑上圆轨道 , 且仍能沿圆轨道滑下 , 求 P 的质量的取值范围 . 【 拓展延伸 】 在 “ 典例 4 ” 的情景中 , 若 P 的质量为 m, 在 B 点有另一小物块 Q,P 到达 B 点时与 Q 发生弹性正碰 , 碰后 Q 离开圆轨道恰好落回 P 开始沿轨道运动的位置 , 求 Q 的质量 M 与 m 的关系 . 【 预测练习 4】 ( 2017 · 湖南株洲一模 ) 如图所示 , 半径为 R 的光滑圆弧轨道 AB 固定在竖直平面内 ,O 为圆心 ,OA 与水平方向的夹角为 30°,OB 在竖直方向 . 一个可视为质点的小球从 O 点正上方某处以某一水平初速度向右抛出 , 小球恰好能无碰撞地从 A 点进入圆轨道内侧 , 此后沿圆轨道运动到达 B 点 . 已知重力加速度为 g, 求 : (1) 小球初速度的大小 ; (2) 小球运动到 B 点时对圆轨道压力的大小 . 答案 : (2)6mg 实战 高考真题演练 1.[ 运动的合成与分解 ]( 2015 · 全国 Ⅱ 卷 ,16 ) 由于卫星的发射场不在赤道上 , 同步卫星发射后需要从转移轨道经过调整再进入地球同步轨道 . 当卫星在转移轨道上飞经赤道上空时 , 发动机点火 , 给卫星一附加速度 , 使卫星沿同步轨道运行 . 已知同步卫星的环绕速度约为 3.1×10 3 m/s, 某次发射卫星飞经赤道上空时的速度为 1.55×10 3 m/s, 此时卫星的高度与同步轨道的高度相同 , 转移轨道和同步轨道的夹角为 30°, 如图所示 . 发动机给卫星的附加速度的方向和大小约为 ( 　 　 ) A. 西偏北方向 ,1.9×10 3 m/s B. 东偏南方向 ,1.9×10 3 m/s C. 西偏北方向 ,2.7×10 3 m/s D. 东偏南方向 ,2.7×10 3 m/s B 2.[ 平抛运动问题 ]( 2017 · 全国 Ⅰ 卷 ,15 ) 发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球 ( 忽略空气的影响 ). 速度较大的球越过球网 , 速度较小的球没有越过球网 ; 其原因是 ( 　 　 ) A. 速度较小的球下降相同距离所用的时间较多 B. 速度较小的球在下降相同距离时在竖直方向上的速度较大 C. 速度较大的球通过同一水平距离所用的时间较少 D. 速度较大的球在相同时间间隔内下降的距离较大 C 3.[ 圆周运动问题 ]( 2016 · 全国 Ⅲ 卷 ,20 ) ( 多选 ) 如图 , 一固定容器的内壁是半径为 R 的半球面 , 在半球面水平直径的一端有一质量为 m 的质点 P. 它在容器内壁由静止下滑到最低点的过程中 , 克服摩擦力做的功为 W. 重力加速度大小为 g. 设质点 P 在最低点时 , 向心加速度的大小为 a, 容器对它的支持力大小为 N, 则 ( 　 　 ) AC 4.[ 平抛与圆周运动的组合问题 ] ( 2017 · 全国 Ⅱ 卷 ,17 ) 如图 , 半圆形光滑轨道固定在水平地面上 , 半圆的直径与地面垂直 . 一小物块以速度 v 从轨道下端滑入轨道 , 并从轨道上端水平飞出 , 小物块落地点到轨道下端的距离与轨道半径有关 , 此距离最大时对应的轨道半径为 ( 重力加速度大小为 g)( 　 　 ) B 点击进入 提升 专题限时检测