【物理】2019届一轮复习人教版 运动的图象、追及相遇问题 学案
第03讲 运动的图象、追及相遇问题
★重难点一、运动的图象★
一、三类运动图像的比较
(1)位移—时间图像反映了做直线运动的物体的位移随时间变化的规律,图像并非物体运动的轨迹。
(2)位移—时间图像只能描述物体做直线运动的情况,这是因为位移—时间图像只能表示物体运动的两个方向:t轴上方代表正方向,t轴下方代表负方向;如果物体做曲线运动,则画不出位移—时间图像。
(3)位移—时间图线上每一点的斜率表示物体该时刻的速度,斜率的大小表示速度的大小,斜率的正负表示速度的方向。
2.位置坐标(x y)图像
表示物体位置的坐标图,图线表示物体实际运动的路线,在坐标图上能表示出物体运动的位移。
3.速度—时间(v t)图像
(1)速度—时间图像反映了做直线运动的物体的速度随时间变化的规律,它也只能描述物体做直线运动的情况。
(2)速度—时间图线上每一点的斜率表示物体该时刻的加速度。
(3)速度—时间图线与t轴所围面积表示这段时间内物体的位移。
二、图像问题的解题思路
用图像来描述两个物理量之间的关系,是物理学中常用的方法,是一种直观且形象的语言和工具。它运用数和形的巧妙结合,恰当地表达各种现象的物理过程和物理规律。运用图像解题的能力可归纳为以下两个方面:
1.读图
即从图象中获取有用信息作为解题的条件,弄清试题中图象所反映的物理过程及规律,从中获取有效信息,一般需要关注的特征量有三个:
第一:关注横、纵坐标
(1)确认横、纵坐标对应的物理量各是什么。
(2)注意横、纵坐标是否从零刻度开始。
(3)坐标轴物理量的单位也不能忽视。
第二:理解斜率、面积、截距的物理意义
(1)图线的斜率:通常能够体现某个物理量的大小、方向及变化情况。
(2)面积:由图线、横轴,有时还要用到纵轴及图线上的一个点或两个点到横轴的垂线段,所围图形的面积,一般都能表示某个物理量,如v t图象中的面积,表示位移。
(3)截距:图线在纵轴上以及横轴上的截距。
第三:分析交点、转折点、渐近线
(1)交点:往往是解决问题的切入点。
(2)转折点:满足不同的函数关系式,对解题起关键作用。
(3)渐近线:往往可以利用渐近线求出该物理量的极值或确定它的变化趋势。
2.作图和用图
依据物体的状态或物理过程所遵循的物理规律,作出与之对应的示意图或数学函数图象来研究和处理问题。
【特别提醒】
运动图象的理解及应用
运动学图象主要有x-t图象和v-t图象,运用运动学图象解题可总结为六看:
x-t图象
v-t图象
轴
横轴为时间t,纵轴为位移x
横轴为时间t,纵轴为速度v
线
倾斜直线表示匀速直线运动
倾斜直线表示匀变速直线运动
斜率
表示速度
表示加速度
面积
无实际意义
图线和时间轴围成的面积表示位移
纵截距
表示初位置
表示初速度
特殊点
拐点表示从一种运动变为另一种运动,交点表示相遇
拐点表示从一种运动变为另一种运动,交点表示速度相等
★重难点二、追及和相遇问题★
一、追及和相遇问题
1.分析追及问题的方法技巧可概括为“一个临界条件”、“两个等量关系”
(1)一个临界条件:速度相等。它往往是物体间能否追上或(两者)距离最大、最小的临界条件,也是分析判断问题的切入点;
(2)两个等量关系:时间关系和位移关系,通过画草图找出两物体的时间关系和位移关系是解题的突破口。
2.能否追上的判断方法
物体B追赶物体A:开始时,两个物体相距x0。若vA=vB时,xA+x0
xB,则不能追上。
3.若被追赶的物体做匀减速直线运动,一定要注意判断追上前该物体是否已经停止运动。
二、追及相遇问题常见的情况
假设物体A追物体B,开始时两个物体相距x0,有三种常见情况:
(1)A追上B时,必有xA-xB=x0,且vA≥vB。
(2)要使两物体恰好不相撞,两物体同时到达同一位置时速度相同,必有xA-xB=x0,vA=vB。
(3)若使两物体保证不相撞,则要求当vA=vB时,xA-xB<x0,且之后vA≤vB。
二、解题思路和方法
⇒⇒⇒
【特别提醒】
求解追及和相遇问题的思路和技巧
(1)解题思路和方法
(2)两点解题技巧
过关检测
一、选择题(本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中. 1~6题只有一项符合题目要求;7~8题有多项符合题目要求。全部选对的得5分,选对但不全的得3分,有选错的得0分。)
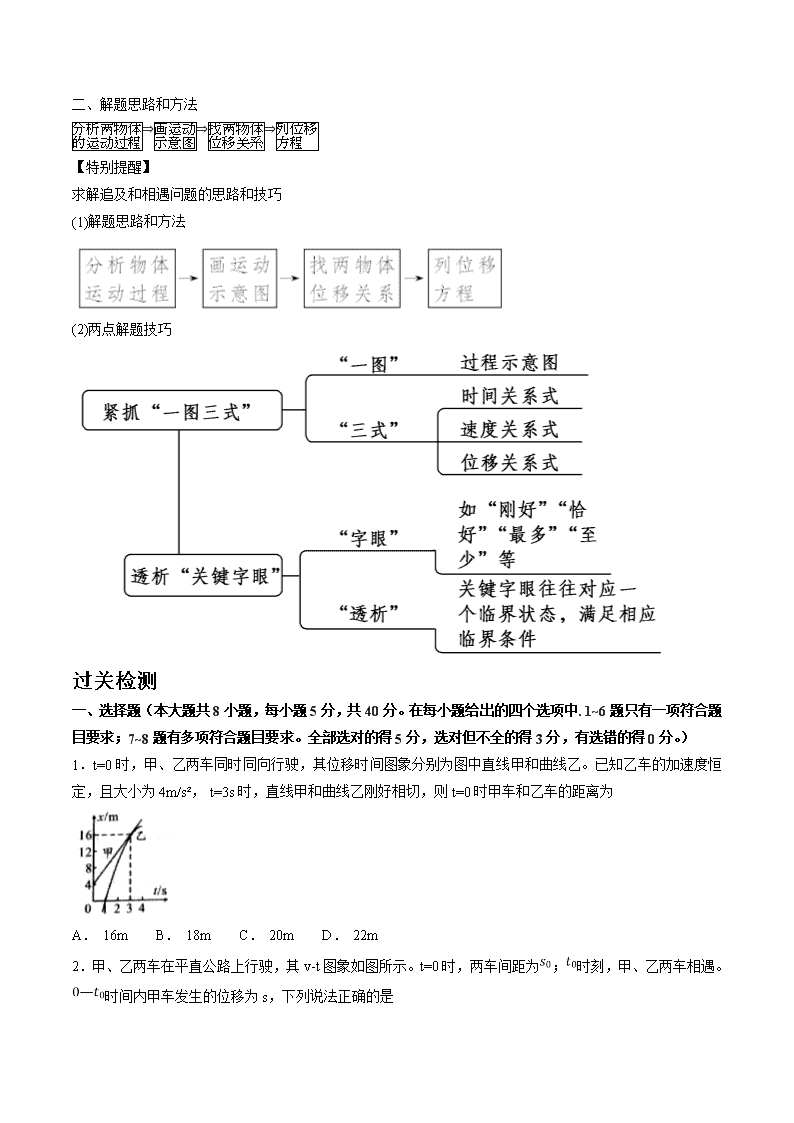
1.t=0时,甲、乙两车同时同向行驶,其位移时间图象分别为图中直线甲和曲线乙。已知乙车的加速度恒定,且大小为4m/s², t=3s时,直线甲和曲线乙刚好相切,则t=0时甲车和乙车的距离为
A. 16m B. 18m C. 20m D. 22m
2.甲、乙两车在平直公路上行驶,其v-t图象如图所示。t=0时,两车间距为;时刻,甲、乙两车相遇。时间内甲车发生的位移为s,下列说法正确的是
A. 时间内甲车在前,时间内乙车在前
B. 时间内甲车平均速度的大小是乙车平均速度大小的2倍
C. 时刻甲、乙两车相距
D.
3.从同一地点先后开出n辆汽车组成车队在平直的公路上行驶,各车均由静止出发先做加速度为a的匀加速直线运动,达到同一速度v后改做匀速直线运动,欲使n辆车都匀速行驶时彼此距离均为s,则各辆车依次启动的时间间隔为(忽略汽车的大小)( )
A. 2v/a
B. v/2a
C. s/2v
D. s/v
4.甲、乙两物体沿同一方向做直线运动,6 s末在途中相遇,它们的速度图象如图所示,可以确定( )
A. t=0时甲在乙的前方54 m处
B. t=0时乙在甲的前方27 m处
C. 6 s之后两物体不会再相遇
D. 6 s之后两物体还会再相遇
5.两个质点A、B放在同一水平面上,从同一位置沿相同方向做直线运动,其运动的v-t图象如图所示.对A、B运动情况的分析,下列结论正确的是
A. 在6s末,质点A的加速度大于质点B的加速度
B. 在0-12s时间内,质点A的平均速度为ms
C. 质点A在0-9s时间内的位移大小等于质点B在0-3s时间内的位移大小
D. 在12s末,A、B两质点相遇
6.如图所示,I、II分别是甲、乙两小球从同一地点沿同一直线运动的v—t图线,根据图线可以判断( )
A. 甲、乙两小球做的是初速度方向相反的匀变速直线运动,加速度大小相同,方向相同
B. 两球在t=8s时相距最远
C. 两球在t=2s时有相同的速度
D. 两球在t=8s时相遇
7.平直的公路上有a、b两辆汽车同向行驶,t=0时刻b车在前a车在后,且辆车相距s0.已知a、b两车的v-t图象如下图所示,在0~t1时间内,b车的位移为s,则下列说法中正确的是( )
A. 0~t1时间内a车的位移为3s
B. 若a、b在t1时刻相遇,则s0=s
C. 若a、b在时刻相遇,则
D. 若a、b在时刻相遇,它们将在时刻再次相遇
8.如图甲乙两车在平直公路上行驶,乙车在甲车前方水平距离为6m处,甲车的初速度为16m/s,乙车的初速度为12m/s,t=0时刻乙车做加速度为lm/s2的匀减速运动,看见乙车减速同时甲车也开始做加速度为2m/s2的匀减速运动,6s后停止减速,下列说法中正确的是
A.t=4s时甲车第一次和乙车并排行驶
B.t=8s时甲车速度和乙车速度大小相等
C.乙车停止运动前,两车共有两次并排行驶过程
D.第一次并排行驶后,两车间水平最大距离为2m
二、非选择题(本大题共2小题,每题10分,共20分)
9.甲乙两车同时同地同向出发,在同一水平公路上做直线运动,甲以初速度v1=16m/s,加速度a1=2m/s2做匀减速运动,乙以初速度v2=4m/s,加速度a2=1m/s2做匀加速运动.求:
(1)两车再次相遇前两者间的最大距离;
(2)两车再次相遇所需的时间.
10.一辆货车正以12m/s的速度在平直公路上前进,发现有货物掉下后,立即松开油门以大小为的加速度做匀减速直线运动,货车开始做匀减速直线运动的同时,在其后面16m处一辆自行车上的人立即拾到货物从静止出发,以的加速度同方向追赶货车,已知自行车能达到的最大速度为8m/s,求:
(1)货车做匀减速运动的位移大小;
(2)自行车至少经过多次时间能追上货车;
参考答案
1、B;2、D;3、D;4、C;5、A;6、D;7、AD;8、CD;
9、【答案】 (1)两车在此相遇前两者间的最大距离为24m;(2)两车在此相遇所需的时间为8s.
【解析】(1)二者相距最远时的特征条件是:速度相等,即v甲t=v乙t
v甲t=v甲-a甲t1;v乙t=v乙+a乙t1,得:t1==4 s
相距最远Δx=x甲-x乙=(v甲t1-a甲t12)-(v乙t1+a乙t12)=24 m。
(2)再次相遇的特征是:二者的位移相等,即
v甲t2-a甲t22=v乙t2+a乙t22,代入数值化简得12t2-t22=0
解得:t2=8 s,t2′=0(即出发时刻,舍去)
10、【答案】 (1) (2)
【解析】(1)已知货车的初速度为,加速度大小为
货车做匀减速运动的时间为
货车做匀减速运动的位移为
(2)已知该自行车的加速度为,最大速度为
自行车做匀加速运动达到最大速度的时间和位移分别为,
之后自行车以最大速度做匀速直线运动,到货车停止运动时,
其位移为,
由于,故货车停止运动时,自行车还没有追上货车,然后自行车继续以最大速度匀速运动追赶货车
由匀速运动的公式得,
代入数据解得
自行车追上货车的时间